WikiDer > Огранка
В геометрия, огранка (также пишется огранка) - это процесс удаления частей многоугольник, многогранник или же многогранник, без создания новых вершины.
Новые ребра граненого многогранника могут быть построены вдоль диагонали лица или внутренний диагонали пространства. А граненый многогранник будет иметь две грани на каждом ребре и создаст новые многогранники или соединения многогранников.
Фасетирование является взаимным или двойной процесс для звездчатость. За каждую звездочку некоторых выпуклый многогранниксуществует двойная огранка двойственный многогранник.
Граненые многоугольники
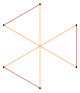
Например, обычный пятиугольник имеет одну грань симметрии, пентаграмма, а обычный шестиугольник имеет две симметричные грани, одну как многоугольник, а другую как соединение двух треугольников.
| Пентагон | Шестиугольник | Декагон | |||||||
|---|---|---|---|---|---|---|---|---|---|
 | 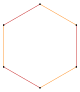 | 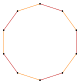 | |||||||
| Пентаграмма {5/2} | Звездный шестиугольник | Сложный 2{3} | Декаграмма {10/3} | Сложный 2{5} | Сложный 2{5/2} | Звездный десятиугольник | |||
 |  | 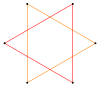 |  |  |  | 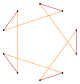 |  | 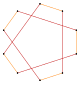 |  |
Граненые многогранники
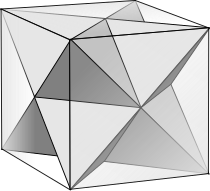
В правильный икосаэдр можно разделить на три обычных Многогранники Кеплера – Пуансо: малый звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. У всех 30 ребер.
| Выпуклый | Обычные звезды | ||
|---|---|---|---|
| икосаэдр | большой додекаэдр | малый звездчатый додекаэдр | большой икосаэдр |
 |  |  |  |
Регулярный додекаэдр можно разделить на одну обычную Многогранник Кеплера – Пуансо, три однородные звездные многогранники, и три правильное полиэдральное соединение. Однородные звезды и соединение пяти кубиков построены диагонали лица. В раскопанный додекаэдр представляет собой огранку с гранями звездообразного шестиугольника.
| Выпуклый | Обычные соединения | ||
|---|---|---|---|
| додекаэдр | пять тетраэдров | пять кубиков | десять тетраэдров |
 |  |  |  |
История
Фасетирование не изучено так широко, как звездчатость.
- В 1568 г. Венцель Ямнитцер опубликовал свою книгу Perspectiva Corporum Regularium, показывающее множество звездчатых и граней многогранников.[1]
- В 1619 г. Кеплер описал регулярное соединение из двух тетраэдры который помещается внутри куба и который он назвал Стелла октангула.
- В 1858 г. Бертран получил регулярный звездные многогранники (Многогранники Кеплера – Пуансо) путем огранки обычный выпуклый икосаэдр и додекаэдр.
- В 1974 году Бридж перечислил более простые аспекты обычный многогранники, в том числе многогранники додекаэдр.
- В 2006 году Инчбальд описал основную теорию диаграмм огранки многогранников. Для данной вершины диаграмма показывает все возможные ребра и фасеты (новые грани), которые можно использовать для формирования граней исходной оболочки. это двойной к двойственный многогранникзвездчатая диаграмма, на которой показаны все возможные ребра и вершины для некоторой плоскости граней исходного ядра.
Рекомендации
Примечания
- ^ Математическое сокровище: Платоновы тела Венцеля Ямницера Фрэнк Дж. Свец (2013): «В этом исследовании пяти Платоновых тел Ямницер усек, звездчатый и ограненный на правильные твердые тела [...]»
Библиография
- Бертран, Дж. Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46 (1858), стр. 79–82.
- Мост, штат Нью-Джерси. Огранка додекаэдра, Acta crystallographica A30 (1974), стр. 548–552.
- Инчбальд, Г. Диаграммы огранки, Математический вестник, 90 (2006), стр. 253–261.
- Алан Холден, Формы, пространство и симметрия. Нью-Йорк: Довер, 1991. с.94.
внешняя ссылка
- Вайсштейн, Эрик В. «Огранка». MathWorld.
- Ольшевский, Георгий. «Огранка». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.