WikiDer > Декаграмма (геометрия)
| Обычная декаграмма | |
|---|---|
 Обычная декаграмма | |
| Тип | Правильный звездный многоугольник |
| Края и вершины | 10 |
| Символ Шлефли | {10/3} т {5/3} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D10) |
| Внутренний угол (градусы) | 72° |
| Двойной многоугольник | себя |
| Характеристики | звезда, циклический, равносторонний, изогональный, изотоксальный |
| Звездные многоугольники |
|---|
В геометрия, а декаграмма это 10 баллов звездный многоугольник. Есть одна правильная декаграмма, содержащая вершины правильный десятиугольник, но связаны каждой третьей точкой. Его Символ Шлефли составляет {10/3}.[1]
Название декаграмма объединяет цифровой префикс, дека-, с Греческий суффикс -грамма. В -грамма суффикс происходит от γραμμῆς (граммы) означает строку.[2]
Обычная декаграмма
Для обычной декаграммы с единичной длиной ребер пропорции точек пересечения на каждом ребре показаны ниже.
Приложения
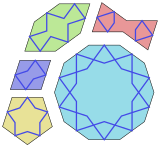
Декаграммы использовались как один из декоративных мотивов в гирих плитки.[3]
Связанные цифры

Обычная декаграмма - это 10-сторонняя полиграмма, представленный символом {10 / n}, содержащий те же вершины, что и обычные десятиугольник. Только одна из этих полиграмм, {10/3} (соединяющая каждую третью точку), образует регулярную звездный многоугольник, но есть еще три десятивершинных полиграммы, которые можно интерпретировать как правильные соединения:
- {10/5} представляет собой соединение пяти вырожденных дигоны 5{2}
- {10/4} представляет собой соединение двух пентаграммы 2{5/2}
- {10/2} представляет собой соединение двух пятиугольники 2{5}.[4][5]
| Форма | Выпуклый | Сложный | Звездный многоугольник | Соединения | |
|---|---|---|---|---|---|
| Изображение |  |  |  |  | 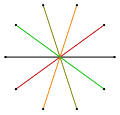 |
| Символ | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
{10/2} можно рассматривать как 2D-эквивалент 3D соединение додекаэдра и икосаэдра и 4D соединение из 120 и 600 ячеек; то есть соединение двух пятиугольные многогранники в их соответствующих двойных позициях.
{10/4} можно рассматривать как двумерный эквивалент трехмерного соединение малого звездчатого додекаэдра и большого додекаэдра или же соединение большого икосаэдра и большого звездчатого додекаэдра по схожим причинам. У нее есть шесть четырехмерных аналогов, два из которых представляют собой соединения двух самодвойственных звездных многогранников, как сама пентаграмма; то соединение двух больших 120-ячеек и соединение двух больших звёздчатых 120-ячеек. Полный список можно увидеть на Составные многогранники # Составы с двойниками.
Более глубокие усечения правильного пятиугольника и пентаграммы могут привести к образованию промежуточных звездообразных многоугольников с десятью равноотстоящими вершинами и двумя длинами ребер, которые остаются вершинно-транзитивный (любые две вершины могут быть преобразованы друг в друга симметрией фигуры).[6][7][8]
| Квазирегулярный | Изогональный | Квазирегулярный Двойное покрытие | |
|---|---|---|---|
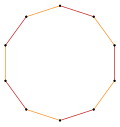 t {5} = {10} | 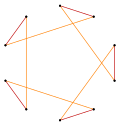 |  |  т {5/4} = {10/4} = 2 {5/2} |
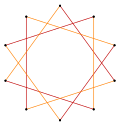 т {5/3} = {10/3} |  | 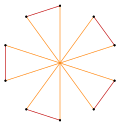 |  t {5/2} = {10/2} = 2 {5} |
Смотрите также
Рекомендации
| Викискладе есть медиафайлы по теме Десятиконечные звезды. |
- ^ Барнс, Джон (2012), Самоцветы геометрии, Springer, стр. 28–29, ISBN 9783642309649.
- ^ γραμμή, Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, на Персее
- ^ Сарханги, Реза (2012), "Многогранная модульность в специальном классе взаимосвязанных звездных многоугольников на основе декаграммы", Мосты 2012: математика, музыка, искусство, архитектура, культура (PDF), стр. 165–174.
- ^ Правильные многогранники, p 93-95, правильные звездчатые многоугольники, правильные звездные соединения
- ^ Кокстер, Введение в геометрию, второе издание, 2.8 Звездные многоугольники стр.36-38
- ^ Светлая сторона математики: Материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум.
- ^ *Коксетер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки.. Королевское общество. 246 (916): 411. Bibcode:1954RSPTA.246..401C. Дои:10.1098 / рста.1954.0003. ISSN 0080-4614. JSTOR 91532. МИСТЕР 0062446.CS1 maint: ref = harv (связь)
- ^ Кокстер, Плотности правильных многогранников I, стр. 43. Если d нечетно, усечение многоугольника {p / q} естественным образом равно {2n / d}. Но если нет, то он состоит из двух совпадающих {n / (d / 2)}; два, потому что каждая сторона возникает из исходной стороны и один раз из исходной вершины. Таким образом, плотность многоугольника не изменяется при усечении.