WikiDer > Дигон - Википедия

Digon - Wikipedia
Для использования в других целях см. Дигон (значения).
Обычный дигон
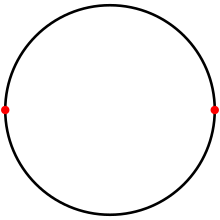Digon.svg
По кругу Digon это мозаика с двумя противоположные точкии две дуговые кромки 180 °.
ТипПравильный многоугольник
Края и вершины2
Символ Шлефли{2}
Диаграмма КокстераCDel node 1.pngCDel 2x.pngCDel node.png
Группа симметрииD2, [2], (*2•)
Двойной многоугольникСамодвойственный

В геометрия, а Digon это многоугольник с двух сторон (края) и два вершины. Его конструкция выродиться в Евклидова плоскость потому что либо две стороны совпадают, либо одна или обе должны быть изогнуты; однако это может быть легко визуализируется в эллиптическом пространстве.

У правильного двуугольника оба угла равны и обе стороны равны, и он представлен Символ Шлефли {2}. Он может быть построен на сфера как пара дуг 180 градусов, соединяющих противоположные точки, когда он образует луна.

Дигон самый простой абстрактный многогранник 2-го ранга.

А усеченный Digon, t {2} - это квадрат, {4}. An чередовались digon, h {2} - это моногон, {1}.

В евклидовой геометрии

Любой прямой Digon является обычный даже если он вырожденный, потому что его два ребра имеют одинаковую длину и два угла равны (оба равны нулю градусов). Таким образом, обычный дигон является конструктивный многоугольник.[1] В этом смысле его можно рассматривать как двойное покрытие отрезка прямой.

Предел генерала осоэдр на сфере можно рассматривать как бесконечный осоэдр, разбиение евклидовой плоскости бесконечным числом двуугольников.[2] Однако вершины этих двуугольников находятся на бесконечности, и, следовательно, эти двуугольники не ограничены замкнутыми отрезками прямых. Эта мозаика обычно не считается дополнительной регулярной мозаикой евклидовой плоскости, даже если ее двойная апейрогональная мозаика порядка 2 (бесконечный диэдр) есть. При формировании такой мозаики двуугольники не напоминают линейные сегменты, а скорее выглядят как бесконечно длинные толстые полосы или «знаки равенства».

В некоторых определениях многоугольника двуугольник не рассматривается как правильный многоугольник из-за его вырождения в евклидовом случае.[3]

В элементарных многогранниках

Неоднородный ромбокубооктаэдр с синими прямоугольными гранями, которые в кубическом пределе вырождаются в двуугольники.

Дигон как лицо из многогранник является выродиться потому что это вырожденный многоугольник. Но иногда он может иметь полезное топологическое существование при преобразовании многогранников.

Как сферическая луна

А сферическая луна двуугольник, две вершины которого противоположные точки на сфере.[4]

А сферический многогранник построенный из таких двуугольников, называется осоэдр.

  • Луна на сфере.

  • Шесть граней двуугольника на правильном шестиугольнике осоэдр.

Теоретическое значение

Дигон - важная конструкция в топологический теория сетей, таких как графы и многогранные поверхности. Топологические эквивалентности могут быть установлены с использованием процесса сведения к минимальному набору многоугольников, не влияя на глобальные топологические характеристики, такие как значение Эйлера. Дигон представляет собой этап упрощения, на котором его можно просто удалить и заменить отрезком линии, не влияя на общие характеристики.

В циклические группы может быть получен как симметрии вращения многоугольников: вращательная симметрия двуугольника обеспечивает группу C2.

Смотрите также

Рекомендации

Цитаты

  1. ^ Эрик Т. Экхофф; Конструируемость правильных многоугольников В архиве 2015-07-14 на Wayback Machine, Университет штата Айова. (Проверено 20 декабря 2015 г.)
  2. ^ Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5, п. 263
  3. ^ Кокстер (1973), Глава 1, Многоугольники и многогранники, стр.4
  4. ^ Кокстер (1973), Глава 1, Многоугольники и многогранники, страницы 4 и 12.

Библиография

внешняя ссылка

  • СМИ, связанные с Дигоны в Wikimedia Commons