WikiDer > Чередование (геометрия)

Чередование куб создает тетраэдр.

Чередование усеченный кубооктаэдр создает неоднородный курносый куб.

В геометрии чередование или частичное усечение, это операция на многоугольник, многогранник, черепица, или более высокое измерение многогранник который удаляет альтернативные вершины.^[1]

Кокстер маркирует чередование с префиксом час, стоя для Hemi или половина. Поскольку при чередовании все грани многоугольника уменьшаются вдвое, его можно применить только к многогранникам со всеми четными гранями. Чередующееся квадратное лицо становится Digon, и будучи вырожденным, обычно сводится к единственному ребру.

В целом любой вершинно-однородный многогранник или мозаика с конфигурация вершины состоящий из всех четных элементов, может быть чередовались. Например, чередование вершинной фигуры с 2a.2b.2c является a.3.b.3.c.3 где тройка - количество элементов в этой вершинной фигуре. Частный случай - квадратные грани, порядок которых делится пополам на вырожденные дигоны. Так, например, куб 4.4.4 чередуется как 2.3.2.3.2.3 который сокращается до 3.3.3, будучи тетраэдр, и все 6 ребер тетраэдров также можно рассматривать как вырожденные грани исходного куба.

Курносый

А пренебрежительно (в Терминология Кокстера) можно рассматривать как чередование из усеченный обычный или усеченный квазирегулярный многогранник. В общем случае многогранник можно пренебречь, если его усечение имеет только четные грани. Все усеченный исправленный многогранники можно обрезать, а не только правильные многогранники.

В курносая квадратная антипризма является примером общего пренебрежения и может быть представлен как ss {2,4} с квадратная антипризма, с {2,4}.

Альтернативные многогранники

Эта чередование операция применима также к многомерным многогранникам и сотам, но в целом результаты этой операции не будут одинаковыми. Пустоты, созданные удаленными вершинами, в общем случае не создают однородных фасетов, и обычно не хватает степеней свободы, чтобы позволить соответствующее изменение масштаба новых ребер. Однако существуют исключения, такие как вывод курносый 24-элементный от усеченный 24-элементный.

Примеры:

• Соты
  1. Альтернативный кубические соты это четырехгранно-октаэдрические соты.
  2. Альтернативный шестиугольные призматические соты это спиральные чередующиеся кубические соты.
• 4-многогранник
  1. Альтернативный усеченный 24-элементный это курносый 24-элементный.
• 4-соты:
  1. Альтернативный усеченные 24-ячеечные соты это курносый 24-элементный сотовый.
• А гиперкуб всегда можно переодеть в форму полугиперкуб.
  1. Куб → Тетраэдр (обычный)
     • →
  2. Тессеракт (8-элементный) → 16 ячеек (обычный)
     • →
  3. Penteract → полусвободный (полурегулярный)
  4. Гексеракт → полугексеракт (униформа)
  5. ...

Измененные многогранники

Коксетер также использовал оператор а, который содержит обе половины, поэтому сохраняет исходную симметрию. Для четных правильных многогранников {2p, q} представляет собой составной многогранник с двумя противоположными копиями h {2p, q}. Для нечетных, больше трех правильных многогранников a {p, q} становится звездный многогранник.

Норман Джонсон расширил использование изменен оператор а{p, q}, б{p, q} для смешанный, и c{p, q} для преобразованный, так как , , и соответственно.

Составной многогранник, известный как звездчатый октаэдр может быть представлен как {4,3} (измененный куб), и , .

Звездный многогранник, известный как малый дитригональный икосододекаэдр может быть представлен как {5,3} (измененный додекаэдр), и , . Здесь все пятиугольники были преобразованы в пентаграммы, а треугольники были вставлены так, чтобы образовались свободные края.

Звездный многогранник, известный как большой дитригональный икосододекаэдр может быть представлен как {5 / 2,3} (измененный большой звездчатый додекаэдр), и , . Здесь все пентаграммы были преобразованы обратно в пятиугольники, а треугольники были вставлены, чтобы занять свободные края.

Альтернативные усечения

Подобная операция может обрезать чередовать вершины, а не просто удалять их. Ниже представлен набор многогранников, которые можно создать из Каталонские твердые вещества. У них есть два типа вершин, которые можно поочередно обрезать. Усечение вершин «более высокого порядка» и обоих типов вершин дает следующие формы:

имя	Оригинал	Альтернативный усечение	Усечение	Усеченное имя
Куб Двойник выпрямленного тетраэдра				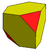Альтернативный усеченный куб
Ромбический додекаэдр Двойственный кубооктаэдра		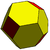		Усеченный ромбический додекаэдр
Ромбический триаконтаэдр Двойник икосододекаэдра				Усеченный ромбический триаконтаэдр
Тетраэдр Триаки Двойник усеченного тетраэдра				Усеченный триакис тетраэдр
Октаэдр Триаки Двойник усеченного куба				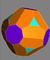Усеченный трехугольный октаэдр
Триакис икосаэдр Двойник усеченного додекаэдра				Усеченный триакис икосаэдр

Смотрите также

• Многогранные обозначения Конвея
• Строительство Wythoff

использованная литература

• Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
• Норман Джонсон Равномерные многогранники, Рукопись (1991)
  • N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
• Вайсштейн, Эрик В. «Оскорбление». MathWorld.
• Ричард Клитцинг, Снабжения, чередующиеся фасетки и диаграммы Стотта-Кокстера-Дынкина, Симметрия: культура и наука, Vol. 21, № 4, 329-344, (2010) [1]

внешние ссылки

• Ольшевский, Георгий. «Чередование». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
• Имена многогранников, курносый

Операторы многогранников

[

• v
• т
• е

]

Семя	Усечение	Исправление	Bitruncation	Двойной	Расширение	Омнитуркация	Чередования
т0{p, q} {p, q}	т01{p, q} т {р, д}	т1{p, q} г {р, д}	т12{p, q} 2t {p, q}	т2{p, q} 2r {p, q}	т02{p, q} рр {р, q}	т012{p, q} tr {p, q}	ht0{p, q} ч {д, р}	ht12{p, q} s {q, p}	ht012{p, q} sr {p, q}