WikiDer > Квадратная антипризма
| Равномерная квадратная антипризма | |
|---|---|
 | |
| Тип | Призматический однородный многогранник |
| Элементы | F = 10, E = 16 V = 8 (χ = 2) |
| Лица по сторонам | 8{3}+2{4} |
| Символ Шлефли | с {2,8} sr {2,4} |
| Символ Wythoff | | 2 2 4 |
| Диаграмма Кокстера | |
| Группа симметрии | D4d, [2+, 8], (2 * 4), порядок 16 |
| Группа вращения | D4, [4,2]+, (442), заказ 8 |
| Рекомендации | U77 (б) |
| Двойной | Тетрагональный трапецоэдр |
| Характеристики | выпуклый |
 Фигура вершины 3.3.3.4 | |
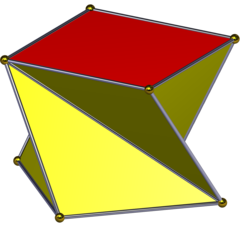
В геометрия, то квадратная антипризма второй в бесконечном наборе антипризмы образованный четной последовательностью сторон треугольника, закрытых двумя крышками многоугольника. Он также известен как антикуб.[1]
Если все его лица обычный, это полуправильный многогранник или же равномерный многогранник.
Неоднородный D4-симметричный вариант - ячейка благородный квадратный антипризматический 72-элементный.
Точки на сфере
Когда восемь точек распределены на поверхности сферы с целью максимизировать расстояние между ними в некотором смысле, результирующая форма соответствует квадратной антипризме, а не куб. Конкретные методы распределения баллов включают, например, Проблема Томсона (минимизация суммы всех обратных расстояний между точками), максимизация расстояния от каждой точки до ближайшей точки или минимизация суммы всех обратных квадратов расстояний между точками.
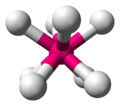
Молекулы с квадратной антипризматической геометрией
Согласно Теория VSEPR из молекулярная геометрия в химии, которая основана на общем принципе максимизации расстояний между точками, квадратная антипризма является предпочтительной геометрией, когда восемь пар электронов окружают центральный атом. Одной молекулой с такой геометрией является ион октафтороксената (VI) (XeF2−
8) в соли октафтороксенат нитрозония (VI); однако молекула отклоняется от идеализированной квадратной антипризмы.[2] Очень немногие ионы имеют кубическую форму, потому что такая форма может вызвать сильное отталкивание между лигандами; PaF3−
8 это один из немногих примеров.[3]
Кроме того, элемент сера образует окатомную S8 молекулы как наиболее стабильные аллотроп. S8 Молекула имеет структуру, основанную на квадратной антипризме, в которой восемь атомов занимают восемь вершин антипризмы, а восемь ребер треугольника-треугольника соответствуют одной ковалентные связи между атомами серы.
В архитектуре
Главный строительный блок Один Всемирный торговый центр (на месте старого Всемирный торговый центр уничтожен на 11 сентября 2001 г.) имеет форму чрезвычайно высокой сужающейся квадратной антипризмы. Это не настоящая антипризма из-за своей конусности: площадь верхнего квадрата составляет половину площади нижнего.
Топологически одинаковые многогранники
Витая призма
А витая призма можно сделать (по часовой стрелке или против часовой стрелки) с тем же расположение вершин. Его можно рассматривать как выпуклую форму с 4 тетраэдры раскопаны по сторонам. Однако после этого его больше нельзя триангулировать в тетраэдры без добавления новых вершин. Он имеет половину симметрия однородного раствора: D4 заказ 4.[4][5]
Скрещенная антипризма
А скрещенная квадратная антипризма это звездный многогранник, топологически идентичный квадратная антипризма с тем же расположение вершин, но его нельзя сделать единообразным; стороны равнобедренные треугольники. Его конфигурация вершины составляет 3.3 / 2.3.4, с одним ретроградным треугольником. Он имеет d4d симметрия, порядок 8.
Связанные многогранники
Производные многогранники
В гировидная квадратная пирамида это Джонсон солид (конкретно, J10), построенный добавлением одного a квадратная пирамида. Точно так же гиродлинная квадратная бипирамида (J17) это дельтаэдр (а многогранник чей лица все равносторонние треугольники), построенный заменой обоих квадратов квадратной антипризмы на квадратную пирамиду.
В курносый дисфеноид (J84) - еще один дельтаэдр, построенный заменой двух квадратов квадратной антипризмы парами равносторонних треугольников. В курносая квадратная антипризма (J85) можно рассматривать как квадратную антипризму с цепочкой равносторонних треугольников, вставленных вокруг середины. В сфенокорона (J86) и сфеномегакорона (J88) - другие тела Джонсона, которые, как и квадратная антипризма, состоят из двух квадратов и четного числа равносторонних треугольников.
В квадратная антипризма можно обрезать и чередовать, чтобы сформировать пренебрежительная антипризма:
| Антипризма | Усеченный т | Альтернативный ht |
|---|---|---|
 с {2,8} |  ts {2,8} |  сс {2,8} |
Мутация симметрии
Как антипризмаквадратная антипризма принадлежит семейству многогранников, включающему октаэдр (которую можно рассматривать как антипризму с треугольной головкой), пятиугольная антипризма, то шестиугольная антипризма, а восьмиугольная антипризма.
| Семья униформы п-гональный антипризмы | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника | ... | Апейрогональная антипризма | ||||||||||||
| Сферическое мозаичное изображение | Плоское мозаичное изображение | |||||||||||||
| Конфигурация вершины п.3.3.3 | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 | |
В квадратная антипризма является первым в серии курносых многогранников и мозаик с вершина фигуры 3.3.4.3.п.
| 4п2 мутации симметрии курносых плиток: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4п2 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гироскоп цифры |  |  |  |  | ||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
Примеры
Один Всемирный торговый центр строительство Квадратная антипризма
(в Matemateca Ime-USP)Плоская квадратная антипризма
(в Математека IME-USP)
Смотрите также
Примечания
- ^ Холлеман-Виберг. Неорганическая химия, Academic Press, Италия, стр. 299. ISBN 0-12-352651-5.
- ^ Петерсон, В .; Holloway, H .; Coyle, A .; Уильямс, М. (сентябрь 1971 г.). «Антипризматическая координация о ксеноне: структура октафтороксената нитрозония (VI)». Наука. 173 (4003): 1238–1239. Bibcode:1971 г., научный ... 173.1238П. Дои:10.1126 / science.173.4003.1238. ISSN 0036-8075. PMID 17775218. S2CID 22384146.
- ^ Гринвуд, Норман Н.; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн. п. 1275. ISBN 978-0-08-037941-8.
- ^ Факты в деле: Справочник по геометрии, Екатерина А. Горини, 2003 г., ISBN 0-8160-4875-4, стр.172
- ^ [1]
внешняя ссылка
- Вайсштейн, Эрик В. «Антипризма». MathWorld.
- Квадратная Антипризма интерактивная модель
- Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
- VRML модель
- Обозначение Конвея для многогранников Попробуйте: «А4»