WikiDer > Триаконтаэдр Дисдякиса
| Триаконтаэдр Дисдякиса | |
|---|---|
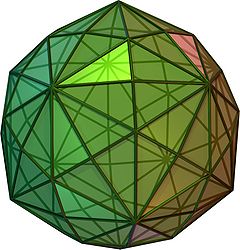 (вращающийся и 3D модель) | |
| Тип | Каталонский |
| Обозначение Конвея | mD или dbD |
| Диаграмма Кокстера | |
| Многоугольник лица |  неравносторонний треугольник |
| Лица | 120 |
| Края | 180 |
| Вершины | 62 = 12 + 20 + 30 |
| Конфигурация лица | V4.6.10 |
| Группа симметрии | ячас, H3, [5,3], (*532) |
| Группа вращения | Я, [5,3]+, (532) |
| Двугранный угол | 164° 53' 17 arccos (-179-24√5/241) |
| Двойной многогранник |  усеченный икосододекаэдр |
| Характеристики | выпуклый, лицо переходный |
 сеть | |
В геометрия, а дисьякис триаконтаэдр, гексакис икосаэдр, декакидодекаэдр или же кисромбический триаконтаэдр[1] это Каталонский твердый со 120 гранями и двойным к Архимедов усеченный икосододекаэдр. Таким образом, это лицо однородное, но с неправильными многоугольниками граней. Немного напоминает надутый ромбический триаконтаэдр- если заменить каждую грань ромбического триаконтаэдра одной вершиной и четырьмя треугольниками, получится триаконтаэдр дисдиакиса. То есть триаконтаэдр Дисдякиса - это Kleetope ромбического триаконтаэдра. Он также имеет наибольшее количество лиц среди архимедовых и каталонских твердых тел, с курносый додекаэдрНа втором месте - 92 лица.
Если бипирамиды, то гиродлинные бипирамиды, а трапецоэдры исключены, триаконтаэдр Дисьякиса имеет наибольшее количество граней любого другого строго выпуклого многогранника, где каждая грань многогранника имеет одинаковую форму.
Спроецированные в сферу ребра триаконтаэдра Дисдякиса определяют 15 большие круги. Бакминстер Фуллер использовал эти 15 больших кругов, а также 10 и 6 других в двух других многогранниках, чтобы определить его 31 большой круг сферического икосаэдра.
Лица
Грани триаконтаэдра дисдякиса представляют собой разносторонние треугольники. Если это Золотое сечение то их углы равны , и .
Симметрия
Ребра многогранника, спроецированные на сферу, образуют 15 большие круги, и представляют все 15 зеркальных плоскостей отражающего ячас икосаэдрическая симметрия. Объединение пар светлых и темных треугольников определяет фундаментальные области неотражающей (я) икосаэдрическая симметрия. Края соединение пяти октаэдров также представляют собой 10 зеркальных плоскостей икосаэдрической симметрии.
 Disdyakis триаконтаэдр |  Дельтовидный гексеконтаэдр |  Ромбический триаконтаэдр |  Додекаэдр |  Икосаэдр |  Пиритоэдр |
| Сферический многогранник | |||
|---|---|---|---|
 |  |  |  |
| (видеть вращающаяся модель) | Ортографические проекции по 2-, 3- и 5-ти осям | ||
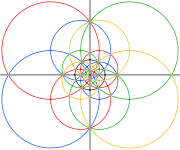
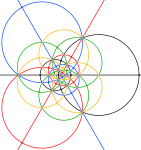
| Стереографические проекции | |||
|---|---|---|---|
 | |||
| 2-кратный | 3-кратный | 5-кратный | |
 |  |  | |
 |  |  | |
| Цвета как соединение пяти октаэдров, с 3 большими кругами для каждого октаэдра. Область в черных кружках ниже соответствует передней полусфере сферического многогранника. | |||
Ортогональные проекции
Триаконтаэдр Дисдякиса имеет три типа вершин, которые могут быть центрированы в ортогональной проекции:
| Проективный симметрия | [2] | [6] | [10] |
|---|---|---|---|
| Изображение | 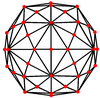 |  |  |
| Двойной изображение |  |  |  |
Использует
В дисьякис триаконтаэдр, как правильный додекаэдр с пятиугольниками, разделенными на 10 треугольников каждый, считается «Святым Граалем» для комбинированные пазлы словно Кубик Рубика. Эта нерешенная проблема, которую часто называют проблемой «большой отбивной», в настоящее время не имеет удовлетворительного механизма. Это самая важная нерешенная проблема в механических головоломках.[2]
Эта форма была использована для создания кубиков d120 с помощью 3D-печати.[3] С 2016 года лаборатория Dice Lab использовала триаконтаэдр Дисьякиса для массового вывода на рынок литых под давлением 120-сторонних умереть.[4] Утверждается, что d120 - это наибольшее количество возможных граней на честном кубике, за исключением бесконечного числа семейств (таких как правильные обычные призмы, бипирамиды, и трапецоэдры), что в действительности было бы непрактично из-за тенденции к катанию в течение длительного времени.[5]
Триконтаэдр дисьякиса проецируется на сферу используется как логотип для Блестящий, веб-сайт, содержащий серию уроков по КОРЕНЬ-похожие темы. [6]
Связанные многогранники и мозаики
 |  |
| Многогранники, подобные триаконтаэдру дисьякиса, двойственны икосаэдру Боути и додекаэдру, содержащим дополнительные пары треугольных граней.[7] | |
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Он топологически связан с последовательностью многогранников, определяемой конфигурация лица V4.6.2n. Эта группа является особенной тем, что у каждой вершины четное число ребер, они образуют биссектрисы, проходящие через многогранники и бесконечные прямые на плоскости, и переходят в гиперболическую плоскость для любого п ≥ 7.
С четным числом граней в каждой вершине эти многогранники и мозаики можно показать, чередуя два цвета, чтобы все смежные грани имели разные цвета.
Каждая грань на этих областях также соответствует фундаментальной области группа симметрии с порядком 2,3,п зеркала в каждой вершине грани треугольника. Это *п32 дюйм орбифолдная запись, и [п, 3] в Обозначение Кокстера.
| *п32 мутации симметрии полностью усеченных мозаик: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п32 [п,3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |  |  |  |  |  |  |  |  |  |  |  |
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Рекомендации
- ^ Конвей, Симметрии вещей, стр.284.
- ^ Big Chop
- ^ Веб-сайт коллекционера кубиков Кевина Кука: d120, напечатанный на 3D-принтере художником Shapeways SirisC
- ^ Лаборатория игры в кости
- ^ http://nerdist.com/this-d120-is-the-largest-mat Mathematically-fair-die-possible/
- ^ "Блестящий | Учитесь думать". brilliant.org. Получено 2020-02-01.
- ^ Симметроэдры: многогранники из симметричного размещения правильных многоугольников Крейг С. Каплан
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, МИСТЕР 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники, Дисдиакистриаконтаэдр)
- Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5 [1] (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, стр. 285, кисРомбический триаконтаэдр)
внешняя ссылка
- Эрик В. Вайсштейн, Триаконтаэдр Дисдякиса (Каталонский твердый) в MathWorld.
- Триаконтаэдр Дисдякиса (Hexakis Icosahedron) - Интерактивная модель многогранника














































