WikiDer > Усеченная трехгексагональная мозаика
| Усеченная трехгексагональная мозаика | |
|---|---|
 | |
| Тип | Полурегулярная черепица |
| Конфигурация вершины |  4.6.12 |
| Символ Шлефли | tr {6,3} или |
| Символ Wythoff | 2 6 3 | |
| Диаграмма Кокстера | |
| Симметрия | p6m, [6,3], (*632) |
| Симметрия вращения | p6, [6,3]+, (632) |
| Акроним Bowers | Othat |
| Двойной | Kisrhombille плитка |
| Характеристики | Вершинно-транзитивный |
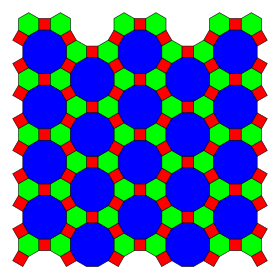
В геометрия, то усеченная трехгексагональная мозаика один из восьми полуправильные мозаики евклидовой плоскости. Есть один квадрат, один шестиугольник, и один двенадцатигранник на каждой вершина. Она имеет Символ Шлефли из tr{3,6}.

Другие имена
- Великолепная ромбитрихексагональная черепица
- Ромбоусеченная трехгексагональная мозаика
- Омниусеченная шестиугольная мозаика, неограниченно усеченная треугольная мозаика
- Конвей называет это усеченный гексаделтил, построенный как усечение операция применяется к трехгексагональная черепица (гексаделтил).[1]
Равномерная окраска
Здесь только один равномерная окраска усеченной трехгексагональной мозаики, грани которой окрашены сторонами многоугольника. 2-равномерная раскраска состоит из двух цветов шестиугольников. 3-однородные раскраски могут иметь 3 цвета двенадцатиугольников или 3 цвета квадратов.
| 1-униформа | 2-униформа | 3-униформа | |||
|---|---|---|---|---|---|
| Окраска |  |  |  |  | |
| Симметрия | p6m, [6,3], (* 632) | p3m1, [3[3]], (*333) | |||
Связанные 2-однородные мозаики
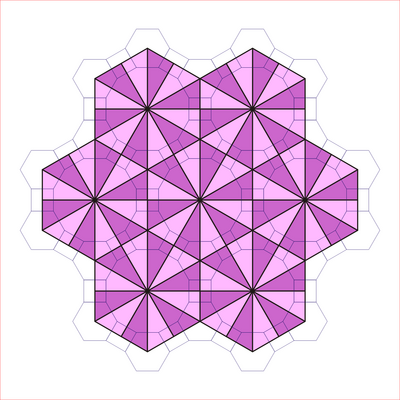
В усеченная трехгексагональная мозаика имеет три связанных 2-однородные мозаики, одна из которых является 2-равномерной раскраской полуправильного ромбитогексагональная черепица. Первый делит шестиугольники на 6 треугольников. Два других рассекают двенадцатиугольники в центральный шестиугольник и окружающие его треугольники и квадрат в двух разных ориентациях.[2][3]
| Полурегулярный | Рассеченный | 2-униформа | 3-униформа |
|---|---|---|---|
 |    |   | 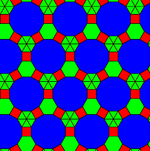  |
| Рассеченный | Полурегулярный | 2-униформа | |
  |   |   |
Упаковка круга
Усеченная трехгексагональная мозаика может использоваться как упаковка круга, поместив круги равного диаметра в центре каждой точки. Каждый круг находится в контакте с 3 другими кругами в упаковке (номер поцелуя).[4]
Kisrhombille плитка
| Kisrhombille плитка | |
|---|---|
 | |
| Тип | Двойной полурегулярный тайлинг |
| Лица | 30-60-90 треугольник |
| Диаграмма Кокстера | |
| Группа симметрии | p6m, [6,3], (* 632) |
| Группа вращения | p6, [6,3]+, (632) |
| Двойной многогранник | усеченная трехгексагональная мозаика |
| Конфигурация лица | V4.6.12 |
| Характеристики | лицо переходный |
В плитка кисромбиль или же 3-6 плиток кисромбилля является замощением евклидовой плоскости. Он построен конгруэнтным 30-60 градусов прямоугольные треугольники с 4, 6 и 12 треугольниками, пересекающимися в каждой вершине.
Конструкция из ромбовидной плитки
Конвей называет это кисромбиль[1] за его поцелуй биссектриса вершины применяется к ромбовидная плитка. Более конкретно его можно назвать 3-6 кисромбиль, чтобы отличать его от других подобных гиперболических мозаик, таких как 3-7 кисромбиль.

Его можно рассматривать как равносторонний шестиугольная черепица с каждым шестиугольником, разделенным на 12 треугольников от центральной точки. (В качестве альтернативы его можно рассматривать как пополам треугольная черепица разделен на 6 треугольников или в виде бесконечного расположение линий в шести параллельных семьях.)
Он помечен как V4.6.12, потому что каждая грань прямоугольного треугольника имеет три типа вершин: один с 4 треугольниками, один с 6 треугольниками и один с 12 треугольниками.
Симметрия
В плитка кисромбиль треугольники представляют фундаментальные области p6m, [6,3] (* 632 орбифолдная запись) группа обоев симметрия. Есть ряд подгруппы малого индекса, построенные из [6,3] удалением и чередованием зеркала. [1+, 6,3] создает симметрию * 333, показанную красными зеркальными линиями. [6,3+] создает симметрию 3 * 3. [6,3]+ - вращательная подгруппа. Коммутаторная подгруппа [1+,6,3+], что соответствует 333 симметрии. Большая подгруппа с индексом 6, построенная как [6,3 *], также становится (* 333), показанной синими зеркальными линиями, и которая имеет свою собственную 333 вращательную симметрию, индекс 12.
| Подгруппы малых индексов [6,3] (* 632) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Индекс | 1 | 2 | 3 | 6 | |||||||
| Диаграмма | 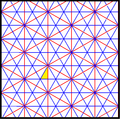 |  |  | 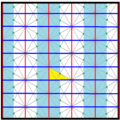 |  | 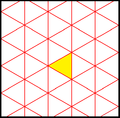 | |||||
| Intl (сфера.) Coxeter | p6m (* 632) [6,3] = | p3m1 (*333) [1+,6,3] = | p31m (3 * 3) [6,3+] = | см (2 * 22) | пмм (*2222) | p3m1 (*333) [6,3*] = | |||||
| Прямые подгруппы | |||||||||||
| Индекс | 2 | 4 | 6 | 12 | |||||||
| Диаграмма |  |  | 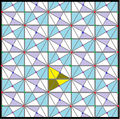 | 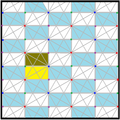 |  | ||||||
| Intl (орб.) Coxeter | p6 (632) [6,3]+ = | п3 (333) [1+,6,3+] = | p2 (2222) | p2 (2222) | п3 (333) [1+,6,3*] = | ||||||
Связанные многогранники и мозаики
Есть восемь однородные мозаики который может быть основан на правильном шестиугольном тайлинге (или двойственном треугольная черепица). Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, можно получить 8 форм, 7 из которых топологически различны. (The усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)
| Однородные шестиугольные / треугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,3], (*632) | [6,3]+ (632) | [6,3+] (3*3) | |||||||||
| {6,3} | т {6,3} | г {6,3} | т {3,6} | {3,6} | рр {6,3} | tr {6,3} | sr {6,3} | с {3,6} | |||
 |  |  |  |  |  |  |  |  | |||
| 63 | 3.122 | (3.6)2 | 6.6.6 | 36 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  |  |  | |||
| V63 | V3.122 | В (3,6)2 | V63 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 | V36 | |||
Мутации симметрии
Этот тайлинг можно рассматривать как член последовательности однородных паттернов с фигурами вершин (4.6.2p) и Диаграмма Кокстера-Дынкина ![]()
![]()
![]()
![]()
![]() . За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.
. За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.
| *п32 мутации симметрии полностью усеченных мозаик: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п32 [п,3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |  |  |  |  |  |  |  |  |  |  |  |
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Смотрите также
| Викискладе есть медиафайлы по теме Равномерная черепица 4-6-12. |
Примечания
- ^ а б Conway, 2008, Глава 21, Именование архимедовых и каталонских многогранников и мозаик, таблица p288
- ^ Чави, Д. (1989). "Тайлинги правильными многоугольниками - II: Каталог мозаик". Компьютеры и математика с приложениями. 17: 147–165. Дои:10.1016/0898-1221(89)90156-9.CS1 maint: ref = harv (связь)
- ^ «Архивная копия». Архивировано из оригинал на 2009-09-09. Получено 2006-09-09.CS1 maint: заархивированная копия как заголовок (связь)
- ^ Порядок в космосе: справочник по дизайну, Кейт Кричлоу, стр.74-75, шаблон D
Рекомендации
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. стр. 41. ISBN 0-486-23729-X.
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]
- Кит Кричлоу, Заказ в космосе: справочник по дизайну, 1970, с. 69-61, Pattern G, Dual p. 77-76, узор 4
- Дейл Сеймур и Джилл Бриттон, Введение в мозаику, 1989, ISBN 978-0866514613, стр. 50–56