WikiDer > Усеченная квадратная мозаика
| Усеченная квадратная мозаика | |
|---|---|
 | |
| Тип | Полурегулярная черепица |
| Конфигурация вершины |  4.8.8 |
| Символ Шлефли | т {4,4} tr {4,4} или |
| Символ Wythoff | 2 | 4 4 4 4 2 | |
| Диаграмма Кокстера | |
| Симметрия | p4m, [4,4], (*442) |
| Симметрия вращения | p4, [4,4]+, (442) |
| Акроним Bowers | Тосквот |
| Двойной | Квадратная плитка Тетракис |
| Характеристики | Вершинно-транзитивный |
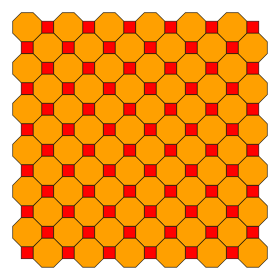
В геометрия, то усеченная квадратная мозаика это полуправильный мозаика правильными многоугольниками из Евклидова плоскость с одним квадрат и два восьмиугольники на каждой вершина. Это единственная мозаика от края до края, выполненная обычный выпуклые многоугольники который содержит восьмиугольник. Она имеет Символ Шлефли из т {4,4}.
Конвей называет это усеченная кадриль, построенный как усечение операция применяется к квадратная черепица (кадриль).
Другие имена, используемые для этого шаблона, включают Средиземноморская черепица и восьмиугольная черепица, который часто представлен меньшими квадратами и неправильными восьмиугольниками, у которых чередуются длинные и короткие края.
Есть 3 обычный и 8 полуправильные мозаики в плоскости.
Равномерная окраска
Есть два разных равномерные раскраски усеченной квадратной мозаики. (Назовите цвета индексами вокруг вершины (4.8.8): 122, 123.)
 2 цвета: 122 |  3 цвета: 123 |
Упаковка круга
Усеченная квадратная мозаика может использоваться как упаковка круга, поместив круги равного диаметра в центре каждой точки. Каждый круг находится в контакте с 3 другими кругами в упаковке (номер поцелуя).[1]
Вариации
Один из вариантов этого шаблона, часто называемый Средиземноморский узор, отображается в виде каменных плиток с меньшими квадратами и по диагонали выровнен с границами. Другие варианты растягивают квадраты или восьмиугольники.
В Пифагорейская черепица чередует большие и маленькие квадраты, и может рассматриваться как топологически идентичный усеченному квадратному мозаичному покрытию. Квадраты повернуты на 45 градусов, а восьмиугольники искажены в квадраты со средними вершинами.
А ткачество шаблон также имеет ту же топологию, с восьмиугольники сплющенный прямоугольники.
| p4m, (* 442) | п4, (442) | p4g, (4 * 2) | pmm (* 2222) | ||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |
| p4m, (* 442) | п4, (442) | см, (2 * 22) | pmm (* 2222) | ||||
 |  |  |  |  |  |  |  |
| Средиземноморье | Пифагорейский | Фламандская облигация | Ткачество | Скрученный | Прямоугольный / ромбический | ||
Связанные многогранники и мозаики

Усеченная квадратная мозаика топологически связана как часть последовательности однородных многогранников и мозаик с фигуры вершин 4.2n.2n, продолжающийся в гиперболической плоскости:
| *п42 мутации симметрии усеченных мозаик: 4,2п.2п | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п42 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Paracomp. | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| Усеченный цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| н-кис цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
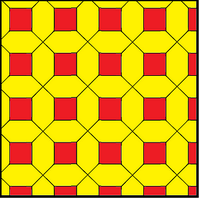
Трехмерный усеченные кубические соты В проекции на плоскость показаны две копии усеченной мозаики. На плоскости он может быть представлен составной плиткой, или комбинированный может рассматриваться как квадратная черепица с фаской.
 |  |  |
Конструкции Wythoff из квадратной черепицы
Рисуя плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, все 8 форм различны. Как бы то ни было, если рассматривать лица одинаково, существует только три уникальных топологически формы: квадратная черепица, усеченная квадратная мозаика, плоская квадратная черепица.
| Равномерные мозаики, основанные на симметрии квадратных мозаик | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [4,4], (*442) | [4,4]+, (442) | [4,4+], (4*2) | |||||||||
 |  |  |  |  |  |  |  | ||||
| {4,4} | т {4,4} | г {4,4} | т {4,4} | {4,4} | рр {4,4} | tr {4,4} | sr {4,4} | с {4,4} | |||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  |  | ||||
| V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.4.4.4 | V4.8.8 | V3.3.4.3.4 | ||||
Связанные мозаики в других симметриях
| *п42 мутации симметрии неусеченных мозаик: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *п42 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | |
| Усеченный фигура |  4.8.4 |  4.8.6 |  4.8.8 |  4.8.10 |  4.8.12 |  4.8.14 |  4.8.16 |  4.8.∞ |
| Усеченный двойники |  V4.8.4 |  V4.8.6 |  V4.8.8 |  V4.8.10 |  V4.8.12 |  V4.8.14 |  V4.8.16 |  V4.8.∞ |
| *nn2 мутации симметрии полностью усеченных мозаик: 4.2п.2п | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *nn2 [п, п] | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||||||||
| *222 [2,2] | *332 [3,3] | *442 [4,4] | *552 [5,5] | *662 [6,6] | *772 [7,7] | *882 [8,8]... | *∞∞2 [∞,∞] | |||||||
| Фигура |  |  |  |  |  |  |  |  | ||||||
| Конфиг. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | ||||||
| Двойной |  |  |  |  |  |  |  |  | ||||||
| Конфиг. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | ||||||
Квадратная плитка Тетракис
В квадратная плитка тетракис есть замощение евклидовой плоскости, двойственное усеченному квадратному замощению. Его можно построить квадратная черепица с каждым квадратом, разделенным на четыре равнобедренный прямоугольные треугольники от центральной точки, образуя бесконечное расположение линий. Его также можно сформировать путем деления каждого квадрата сетки на два треугольника по диагонали, при этом диагонали чередуются по направлению, или путем наложения двух квадратных сеток, одна из которых повернута на 45 градусов относительно другой и масштабирована с коэффициентом √2.
Конвей называет это кисвадриль,[2] представлен поцелуй операция, которая добавляет центральную точку и треугольники для замены граней квадратная черепица (кадриль). Его еще называют Решетка Юнион Джек из-за сходства с Флаг Великобритании треугольников, окружающих его вершины степени 8.[3]
Смотрите также
| Викискладе есть медиафайлы по теме Равномерная черепица 4-8-8. |
Рекомендации
- ^ Порядок в космосе: исходник по дизайну, Кейт Кричлоу, стр.74-75, круговой узор H
- ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 «Архивная копия». Архивировано из оригинал в 2010-09-19. Получено 2012-01-20.CS1 maint: заархивированная копия как заголовок (связь) (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, таблица с. 288)
- ^ Стивенсон, Джон (1970), "Модель Изинга с антиферромагнитной связью ближайших соседей: спиновые корреляции и точки нарушения", Phys. Ред. B, 1 (11): 4405–4409, Дои:10.1103 / PhysRevB.1.4405.
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]
- Грюнбаум, Бранко И Шепард, Г.С. (1987). Плитки и узоры. Нью-Йорк: У. Х. Фриман. ISBN 0-7167-1193-1. (Глава 2.1: Регулярные и однородные мозаики, п. 58-65)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. стр. 40. ISBN 0-486-23729-X.
- Дейл Сеймур и Джилл Бриттон, Введение в мозаику, 1989, ISBN 978-0866514613, стр. 50–56





