WikiDer > Пятиугольная черепица

В геометрия, а пятиугольная черепица это облицовка плоскости где каждая отдельная деталь имеет форму пятиугольник.
А обычный пятиугольник облицовка Евклидова плоскость невозможно, потому что внутренний угол из правильный пятиугольник, 108 °, не является делителем 360 °, угловой меры целого повернуть. Однако правильные пятиугольники могут выложить гиперболическая плоскость и сфера; последний порождает мозаику, топологически эквивалентную додекаэдр.
Моноэдральные выпуклые пятиугольные мозаики
Известно пятнадцать типов выпуклых пятиугольников, покрывающих плоскость. моноэдрально (т.е. с одним типом плитки).[1] Самый последний из них был обнаружен в 2015 году. Этот список был подтвержден Рао (2017) (результат подлежит экспертной оценке). Багина (2011) показал, что всего восемь от края до края выпуклые типы, результат, полученный независимо Сугимото (2012).
Микаэль Рао из École normale supérieure de Lyon в мае 2017 года заявили, что нашли доказательство того, что на самом деле не существует выпуклых пятиугольников, выходящих за пределы этих 15 типов.[2] По состоянию на 11 июля 2017 г. первая половина доказательства Рао была проверена независимо (имеется компьютерный код).[3]) Томаса Хейлза, профессора математики Питтсбургского университета.[4] По состоянию на декабрь 2017 года доказательства еще не прошли полную рецензию.
Каждое перечисленное семейство листов содержит пятиугольники, не принадлежащие ни к какому другому типу; однако некоторые отдельные пятиугольники могут принадлежать к нескольким типам. Кроме того, некоторые из пятиугольников в известных типах листов также допускают альтернативные шаблоны мозаики помимо стандартной мозаики, представленной всеми членами этого типа.
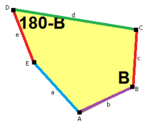
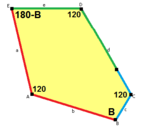
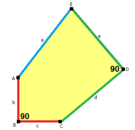
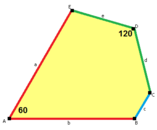
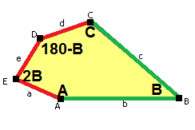
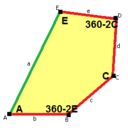
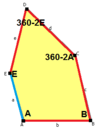
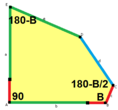
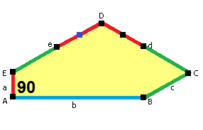
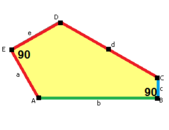
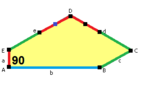
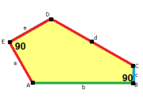
Стороны длины а, б, c, d, е находятся прямо по часовой стрелке от углов при вершинах А, B, C, D, E соответственно. (Таким образом,А, B, C, D, E противоположны d, е, а, б, c соответственно.)
Многие из этих типов одногранной плитки имеют степени свободы. Эти свободы включают варианты внутренние углы и длины кромок. В пределе края могут иметь длину, приближающуюся к нулю, или углы, приближающиеся к 180 °. Типы 1, 2, 4, 5, 6, 7, 8, 9 и 13 позволяют параметрические возможности с невыпуклыми прототипами.
Периодические мозаики характеризуются группа обоев симметрия, например p2 (2222) определяется четырьмя точками двукратного вращения. Эта номенклатура используется на диаграммах ниже, где плитки также окрашены в соответствии с их k-изоэдральный позиции в пределах симметрии.
А примитивная единица - это минимально возможная часть мозаики, которая генерирует всю мозаику с использованием только переводов.
Рейнхардт (1918)
Рейнхардт (1918) нашли первые пять видов пятиугольной плитки. Все пятеро могут создавать равногранный мозаики, что означает, что симметрии мозаики могут привести любую плитку к любой другой плитке (более формально группа автоморфизмов действует транзитивно на плитке).
Б. Грюнбаум и Г. К. Шепард показали, что существует ровно двадцать четыре различных «типа» равногранных мозаик плоскости пятиугольниками в соответствии с их классификационной схемой.[5] Все используют плитки Рейнхардта, обычно с дополнительными условиями, необходимыми для облицовки. Есть две мозаики всех плиток типа 2 и по одной плитки всех остальных четырех типов. Пятнадцать из остальных восемнадцати плиток относятся к частным случаям плиток типа 1. Девять из двадцати четырех плиток - от края до края.[6]
Существуют также 2-равногранные мозаики частными случаями плиток типа 1, типа 2 и 4, а также 3-равногранные мозаики, все рёберные, на особые случаи плиток типа 1. Не существует верхней границы k для k-изоэдральных мозаик определенными плитками, которые относятся как к типу 1, так и к типу 2, и, следовательно, ни на количество плиток в примитивной единице.
В группа обоев симметрия для каждого тайлинга дана, с орбифолдная запись в скобках. Вторая более низкая группа симметрии дается, если плитка хиральность существует, где зеркальные изображения считаются различными. В таких случаях они отображаются желтыми и зелеными плитками.
Тип 1
Существует множество мозаичных топологий, содержащих пятиугольники типа 1. Ниже приведены пять примеров топологий.
| p2 (2222) | см (2 * 22) | см (* ×) | pmg (22 *) | пгг (22 ×) | p2 (2222) | см (2 * 22) |
|---|---|---|---|---|---|---|
| p1 (°) | p2 (2222) | p2 (2222) | ||||
 |  |  |  |  |  |  |
| 2-х плитный примитив | Примитивный блок из 4 плиток | |||||
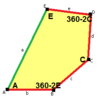
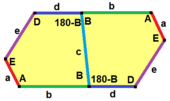 В + С = 180 ° A + D + E = 360 ° |  а = с, д = е А + В = 180 ° C + D + E = 360 ° | 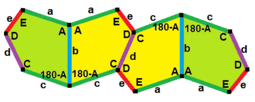 а = с А + В = 180 ° C + D + E = 360 ° | 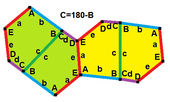 а = е В + С = 180 ° A + D + E = 360 ° | 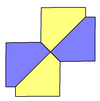 d = c + e А = 90 °, 2В + С = 360 ° C + D = 180 °, B + E = 270 ° | ||
Тип 2
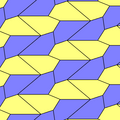
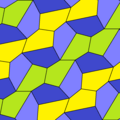
Эти примеры типа 2 изоэдральны. Второй вариант - от края до края. Оба они обладают симметрией pgg (22 ×). Если зеркальные отражательные плитки (желтый и зеленый) считаются разными, симметрия равна p2 (2222).
| пгг (22 ×) | |
|---|---|
| p2 (2222) | |
 |  |
| Примитивный блок из 4 плиток | |
 с = е B + D = 180 ° | 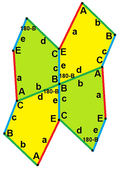 c = e, d = b B + D = 180 ° |
Типы 3, 4 и 5
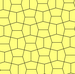
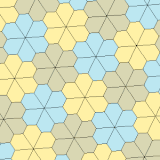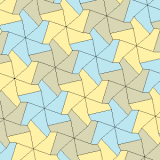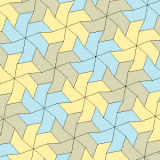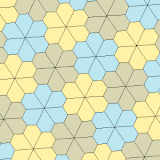
| Тип 3 | Тип 4 | Тип 5 | ||||
|---|---|---|---|---|---|---|
| п3 (333) | p31m (3 * 3) | п4 (442) | p4g (4 * 2) | p6 (632) | ||
 |  |  |  |  |  | |
 |  |  | ||||
| Примитивный блок из 3 плиток | Примитивный блок из 4 плиток | 6-ти тайловый примитив | Примитивный блок из 18 плиток | |||
 а = б, д = с + е А = С = D = 120 ° | 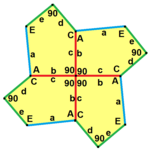 б = с, г = д B = D = 90 ° | 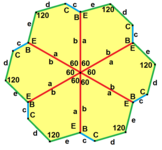 а = б, г = д А = 60 °, D = 120 ° |  а = б = с, д = е A = 60 °, B = 120 °, C = 90 ° D = 120 °, E = 150 ° | |||
Кершнер (1968) Типы 6, 7, 8
Кершнер (1968) нашли еще три типа пятиугольной плитки, в результате чего общее количество достигло восьми. Он ошибочно утверждал, что это был полный список пятиугольников, которые могут выложить плоскость.
Эти примеры являются 2-равногранными и сквозными. Типы 7 и 8 имеют хиральные пары плиток, которые окрашены в пары желто-зеленого цвета, а остальные - в два оттенка синего. Симметрия pgg снижается до p2, когда киральные пары считаются различными.
Джеймс (1975) Тип 10
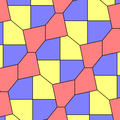
В 1975 году Ричард Э. Джеймс III обнаружил девятый тип, прочитав о результатах Кершнера в Мартин Гарднер"s"Математические игры"столбец в Scientific American журнал от июля 1975 г. (перепечатано в Гарднер (1988)). Он индексируется как тип 10. Мозаика является 3-равногранной и не сквозной.
| p2 (2222) | см (2 * 22) |
|---|---|
 |  |
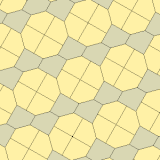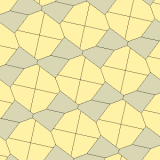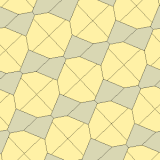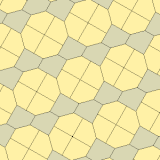 | |
 а = б = с + е А = 90, В + Е = 180 ° B + 2C = 360 ° | 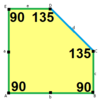 а = b = 2c = 2e A = B = E = 90 ° C = D = 135 ° |
 6-ти тайловый примитив | |
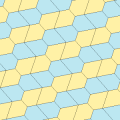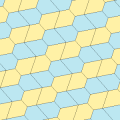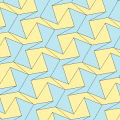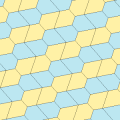
Рис (1977) Типы 9,11,12,13
Марджори Райсматематик-любитель открыл четыре новых типа мозаика пятиугольники в 1976 и 1977 гг.[6][7]
Все четыре мозаики 2-равногранны. Хиральные пары плиток окрашены в желтый и зеленый цвета для одного равногранного набора и два оттенка синего для другого набора. Симметрия pgg снижается до p2, когда киральные пары считаются различными.
Укладка плиткой типа 9 идет от края до края, а остальные - нет.
Каждая примитивная единица содержит восемь плиток.
Stein (1985) Тип 14
14-й тип выпуклого пятиугольника был обнаружен Рольфом Штайном в 1985 году.[8]
Мозаика 3-равногранная и не сквозная. Он имеет полностью определенные плитки без степеней свободы. Точные пропорции указаны и угол B тупой с . Легко вывести другие отношения.
Примитивные блоки содержат шесть плиток соответственно. Он имеет симметрию p2 (2222).
 | 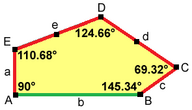 2a = 2c = d = e A = 90 °, B≈145,34 °, C≈69,32 °, D≈124,66 °, E≈110,68 ° (2B + C = 360 °, C + E = 180 °). | 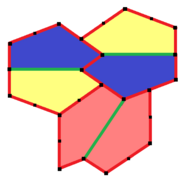 6-ти тайловый примитив |
Манн / Маклауд / Фон Дерау (2015) Тип 15
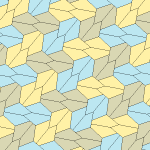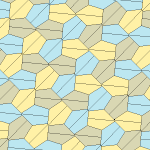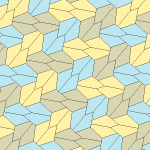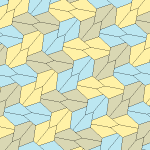
Вашингтонский университет Ботелла математики Кейси Манн, Дженнифер Маклауд-Манн, а Дэвид фон Дерау открыл 15-й моноэдрический мозаичный выпуклый пятиугольник в 2015 году, используя компьютерный алгоритм.[9][10] Он 3-равногранный и не сквозной, нарисованный 6 цветами, 2 оттенками 3 цветов, представляющими хиральные пары трех равногранных позиций. Симметрия pgg снижается до p2, когда киральные пары считаются различными. Он имеет полностью определенные плитки без степеней свободы. Примитивные блоки содержат соответственно двенадцать плиток. Он имеет симметрию pgg (22 ×) и p2 (2222), если киральные пары считаются различными.
В июле 2017 года Михаэль Рао завершил компьютерное доказательство, показывающее, что нет других типов выпуклых пятиугольников, которые могли бы выложить плоскость. Полный список выпуклых многоугольников, которые могут покрывать плоскость, включает указанные выше 15 пятиугольников, три типа шестиугольников и все четырехугольники и треугольники.[4] Следствием этого доказательства является то, что не существует выпуклого многоугольника, который бы мозаично делил плоскость только апериодически, поскольку все вышеперечисленные типы допускают периодическое мозаичное покрытие.
 (Изображение большего размера) |  a = c = e, b = 2a, d =а+√2/√3-1 A = 150 °, B = 60 °, C = 135 ° D = 105 °, E = 90 ° | 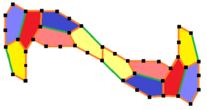 Примитивный блок из 12 плиток |
Непериодические моноэдральные мозаики пятиугольников
Непериодические моноэдральные пятиугольные мозаики также могут быть построены, как в приведенном ниже примере, с 6-кратными вращательная симметрия пользователя Michael Hirschhorn. Углы: A = 140 °, B = 60 °, C = 160 °, D = 80 °, E = 100 °.[11][12]
В 2016 году Бернхард Клаассен смог показать, что каждый дискретный тип вращательной симметрии может быть представлен моноэдральным пятиугольным замощением из того же класса пятиугольников.[13] Примеры 5-кратной и 7-кратной симметрии показаны ниже. Такие мозаики возможны для любого типа п-кратная вращательная симметрия с п>2.
Двойные однородные мозаики
Есть три равногранный пятиугольные мозаики, порожденные как двойники из однородные мозаики, с 5-валентными вершинами. Они представляют собой особые случаи высшей симметрии 15 моноэдральных мозаик, указанных выше. Однородные мозаики и их двойники - все сквозные. Эти двойственные мозаики также называют Лавес плитки. Симметрия однородных двойственных мозаик такая же, как и у равномерных мозаик. Поскольку однородные мозаики изогональный, двойники равногранный.
| см (2 * 22) | p4g (4 * 2) | p6 (632) |
|---|---|---|
 | 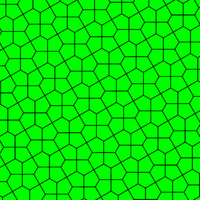 |  |
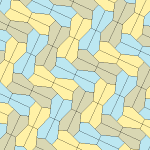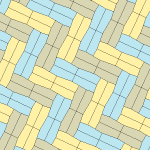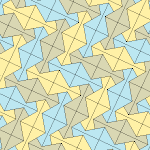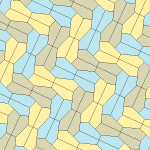
| Призматическая пятиугольная черепица Экземпляр Тип 1[14] | Каир пятиугольная черепица Экземпляр тип 4[14][15] | Пятиугольная черепица Floret Экземпляр типы 1, 5 и 6[14] |
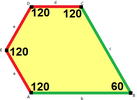
 120°, 120°, 120°, 90°, 90° V3.3.3.4.4 | 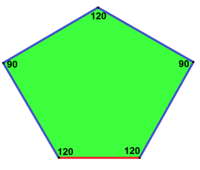 120°, 120°, 90°, 120°, 90° V3.3.4.3.4 | 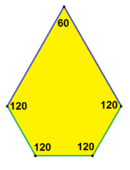 120°, 120°, 120°, 120°, 60° V3.3.3.3.6 |
Двойной k-однородные мозаики
В k-однородные мозаики вершины с валентностью-5 также имеют пятиугольные двойственные мозаики, содержащие те же трехугольные пятиугольники, что и полуправильные дуальные элементы выше, но содержат смесь пятиугольных типов. А k-однородная мозаика имеет k-изоэдральная двойная черепица и представлены ниже разными цветами и оттенками цветов.
Например, эти 2, 3, 4 и 5-однородные двойники пятиугольные:[16][17]
| 2-равногранный | 3-равногранный | |||
|---|---|---|---|---|
| p4g (4 * 2) | пгг (22 ×) | p2 (2222) | p6 (* 632) | |
 |  |  |  |  |
| 4-равногранный | 5-равногранный | |||
| пгг (22 ×) | p2 (2222) | p6m (* 632) | ||
 |  |  |  |  |
| 5-равногранный | ||||
| пгг (22 ×) | p2 (2222) | |||
 |  |  |  |  |
Пятиугольная / шестиугольная мозаика
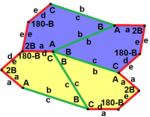
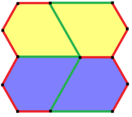
Пентагоны имеют особые отношения с шестиугольниками. Как показано ниже графически, некоторые типы шестиугольников можно разделить на пятиугольники. Например, правильный шестиугольник делится пополам на два пятиугольника типа 1. Также возможно разделение выпуклых шестиугольников на три (тип 3), четыре (тип 4) и девять (тип 3) пятиугольников.
Расширяя это соотношение, плоскость может быть замощена одной пятиугольной формой прототипа способами, которые создают шестиугольные наложения. Например:
Невыпуклые пятиугольники
С пятиугольниками, которые необязательно выпуклыйвозможны дополнительные виды облицовки. Примером может служить плитка сфинкс, апериодическая мозаика образованный пятиугольником реплика.[18] Сфинкс также может периодически мозаить плоскость, соединяя две плитки сфинкса вместе, чтобы сформировать параллелограмм а затем замощить плоскость сдвигами этого параллелограмма,[18] узор, который может быть расширен до любого невыпуклого пятиугольника, который имеет два последовательных угла, добавляющих к 2π, таким образом удовлетворяя условию (ям) выпуклости Тип 1 над.
Можно разделить равносторонний треугольник на три конгруэнтных невыпуклых пятиугольника, встречающихся в центре треугольника, и соединить плоскость плиткой с полученной единицей трех пятиугольников.[19]Аналогичный метод можно использовать для подразделения квадраты на четыре конгруэнтных невыпуклых пятиугольника, или правильные шестиугольники на шесть конгруэнтных невыпуклых пятиугольников, а затем выложите плоскость получившейся единицей.
Правильные пятиугольные мозаики в неевклидовой геометрии
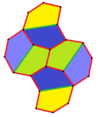
А додекаэдр можно рассматривать как правильную мозаику из 12 пятиугольников на поверхности сфера, с Символ Шлефли {5,3} с тремя пятиугольниками вокруг каждой вершины.
в гиперболическая плоскость, есть мозаики правильных пятиугольников, например Пятиугольная черепица порядка 4, {5,4} с четырьмя пятиугольниками вокруг каждой вершины. Регулярные мозаики более высокого порядка {5, n} могут быть построены на гиперболической плоскости, заканчивающейся на {5, ∞}.
| Сфера | Гиперболическая плоскость | |||||
|---|---|---|---|---|---|---|
 {5,3} |  {5,4} |  {5,5} |  {5,6} |  {5,7} |  {5,8} | ...{5,∞} |
Неправильные гиперболические плоские пятиугольные мозаики
Есть бесконечное количество двойных равномерные мозаики в гиперболической плоскости с изогональными неправильными пятиугольными гранями. У них есть конфигурации лица как V3.3.п.3.q.
| 7-3 | 8-3 | 9-3 | ... | 5-4 | 6-4 | 7-4 | ... | 5-5 |
|---|---|---|---|---|---|---|---|---|
 V3.3.3.3.7 |  V3.3.3.3.8 | V3.3.3.3.9 | ... |  V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | ... | V3.3.5.3.5 |

В двоичная мозаика можно превратить в пятиугольную мозаику, если заменить орициклические ребра отрезками прямых.
Рекомендации
- ^ Грюнбаум и Шепард 1987, Разд. 9.3. Другие моноэдральные мозаики выпуклыми многоугольниками.
- ^ Рао 2017.
- ^ "Код Mathematica, проверяющий классификацию выпуклых пятиугольников Рао", GitHub
- ^ а б Wolchover 2017.
- ^ Грюнбаум и Шепард 1978.
- ^ а б Schattschneider 1978.
- ^ Марджори Райс, «Тесселяции», Интригующие мозаики, получено 22 августа 2015 - через Сайты Google
- ^ Schattschneider 1985.
- ^ Беллос 2015.
- ^ Манн, Маклауд-Манн и фон Дерау 2018.
- ^ Schattschneider 1978, Рис 12.
- ^ Хиршхорн и Хант 1985.
- ^ Клаассен 2016.
- ^ а б c Рейнхардт 1918, стр.77–81 (Внимание: в этой статье есть как минимум одна очевидная ошибка, т.е. сумма углов γ + δ должна равняться π, а не 2π для первых двух типов мозаики, определенных на странице 77)
- ^ Пятиугольная мозаика Каира, порожденная пятиугольник 4 запрос и по пятиугольник 2 черепица запрос на wolframalpha.com (осторожно: определение вольфрама пятиугольник тип 2 черепица не соответствует тип 2 определен Райнхардтом в 1918 г.)
- ^ Чави 1989.
- ^ Брайан Галебах, "Добро пожаловать в мою коллекцию n-однородных мозаик!", вероятностьsports.com
- ^ а б Годреш 1989.
- ^ Гервер 2003.
Библиография
- Багина, Ольга (2004), "Замощение плоскости конгруэнтными равносторонними выпуклыми пятиугольниками", Журнал комбинаторной теории, серия А, 105 (2): 221–232, Дои:10.1016 / j.jcta.2003.11.002, ISSN 1096-0899, МИСТЕР 2046081
- Багина, Ольга (2011), Мозаики из выпуклых пятиугольников [Замощения плоскости выпуклыми пятиугольниками], Вестник (на русском), 4 (48): 63–73, ISSN 2078-1768, получено 29 января 2013
- Беллос, Алекс (11 августа 2015 г.), «Атака на пятиугольник приводит к открытию новой математической плитки», Хранитель
- Чави, Д. (1989), "Тайлинги правильными многоугольниками - II: Каталог мозаик", Компьютеры и математика с приложениями, 17 (1–3): 147–165, Дои:10.1016/0898-1221(89)90156-9
- Гарднер, Мартин (1988), «Мозаика с выпуклыми многоугольниками», Путешествие во времени и прочие математические недоумения, Нью-Йорк: W.H. Фриман, Bibcode:1988ttom.book ..... G, ISBN 978-0-7167-1925-0, МИСТЕР 0905872
- Гервер, М. Л. (2003), "Теоремы о мозаике многоугольниками", Сборник: математика, 194 (6): 879–895, Bibcode:2003СбМат.194..879Г, Дои:10.1070 / см2003v194n06abeh000743
- Годреш, К. (1989), "Сфинкс: предельно-периодическая мозаика плоскости", Журнал физики A: математические и общие, 22 (24): L1163 – L1166, Bibcode:1989JPhA ... 22L1163G, Дои:10.1088/0305-4470/22/24/006, МИСТЕР 1030678
- Грюнбаум, Бранко; Шепард, Джеффри К. (1978), "Изоэдральные мозаики плоскости многоугольниками", Комментарии Mathematici Helvetici, 53: 542–571, Дои:10.1007 / bf02566098, ISSN 0010-2571
- Грюнбаум, Бранко; Шепард, Джеффри К. (1987), "Замощение полигонов", Плитки и узоры, Нью-Йорк: W. H. Freeman and Company, ISBN 978-0-7167-1193-3, МИСТЕР 0857454
- Hirschhorn, M.D .; Хант, Д. К. (1985), «Равносторонние выпуклые пятиугольники, покрывающие плоскость» (PDF), Журнал комбинаторной теории, серия А, 39 (1): 1–18, Дои:10.1016/0097-3165(85)90078-0, ISSN 1096-0899, МИСТЕР 0787713, получено 2020-10-30
- Кершнер, Ричард (1968), "На асфальте самолета", Американский математический ежемесячный журнал, 75 (8): 839–844, Дои:10.2307/2314332, ISSN 0002-9890, JSTOR 2314332, МИСТЕР 0236822
- Клаассен, Бернхард (2016), "Вращательно-симметричные мозаики с выпуклыми пятиугольниками и шестиугольниками", Elemente der Mathematik, 71 (4): 137–144, arXiv:1509.06297, Дои:10,4171 / см / 310, ISSN 0013-6018
- Манн, Кейси; Маклауд-Манн, Дженнифер; Фон Дерау, Дэвид (2018), «Выпуклые пятиугольники, допускающие -блочные переходные мозаики ", Geometriae Dedicata, 194 (1): 141–167, arXiv:1510.01186, Дои:10.1007 / s10711-017-0270-9
- Рао, Михаэль (2017), Исчерпывающий поиск выпуклых пятиугольников, покрывающих плоскость (PDF), arXiv:1708.00274
- Рейнхардт, Карл (1918), Über die Zerlegung der Ebene in Polygone (Диссертация) (на немецком языке), Борна-Лейпциг: Druck von Robert Noske
- Шатчнайдер, Дорис (1978), "Покрытие плоскости равными пятиугольникам", Математический журнал, 51 (1): 29–44, Дои:10.2307/2689644, ISSN 0025-570X, JSTOR 2689644, МИСТЕР 0493766
- Шатчнайдер, Дорис (1985), «Новый пятиугольник», Математический журнал, 58 (5): 308, На обложке изображен новый кафель.
- Сугимото, Терухиса; Огава, Тору (2005), «Систематическое изучение выпуклых пятиугольных мозаик. I. Случай выпуклых пятиугольников с четырьмя ребрами равной длины», Forma, 20: 1–18, МИСТЕР 2240616
- Сугимото, Терухиса; Огава, Тору (2009), «Систематическое изучение выпуклых пятиугольных мозаик, II: мозаики выпуклыми пятиугольниками с четырьмя ребрами равной длины», Forma, 24 (3): 93–109, МИСТЕР 2868775; Опечатки, Forma 25 (1): 49, 2010, МИСТЕР2868824
- Сугимото, Терухиса (2012), «Выпуклые пятиугольники для мозаики от края до края, I», Forma, 27 (1): 93–103, МИСТЕР 3030316
- Вулховер, Натали (11 июля 2017 г.), "Pentagon Tiling Proof решает вековую математическую проблему", Журнал Quanta
внешняя ссылка
| Викискладе есть медиафайлы по теме Пятиугольные мозаики. |