WikiDer > Восьмиугольная черепица
| Восьмиугольная черепица | |
|---|---|
 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболический правильный тайлинг |
| Конфигурация вершины | 83 |
| Символ Шлефли | {8,3} т {4,8} |
| Символ Wythoff | 3 | 8 2 2 8 | 4 4 4 4 | |
| Диаграмма Кокстера | |
| Группа симметрии | [8,3], (*832) [8,4], (*842) [(4,4,4)], (*444) |
| Двойной | Треугольная черепица Order-8 |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный, лицо переходный |
В геометрия, то восьмиугольная черепица это обычная черепица из гиперболическая плоскость. Он представлен Символ Шлефли из {8,3}, имея три обычных восьмиугольники вокруг каждой вершины. Он также имеет конструкцию в виде усеченной квадратной мозаики порядка 8, t {4,8}.
Равномерная окраска
Словно шестиугольная черепица евклидовой плоскости есть 3 равномерные раскраски этого гиперболического разбиения. Двойная мозаика V8.8.8 представляет собой фундаментальные области симметрии [(4,4,4)].
| Обычный | Усечения | ||
|---|---|---|---|
 {8,3} | 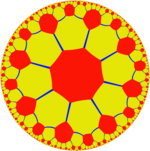 т {4,8} |  т {4[3]} | |
| Двойная черепица | |||
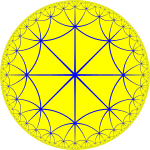 {3,8} |  |  | |
Связанные многогранники и мозаики
Эта мозаика топологически является частью последовательности правильных многогранников и мозаик с Символ Шлефли {n, 3}.
| *п32 изменения симметрии правильных мозаик: {п,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
А также является топологически частью последовательности правильных мозаик с Символ Шлефли {8, н}.
| Космос | Сферический | Компактный гиперболический | Паракомпакт | |||||
|---|---|---|---|---|---|---|---|---|
| Плитка |  |  |  |  |  |  |  | |
| Конфиг. | 8.8 | 83 | 84 | 85 | 86 | 87 | 88 | ...8∞ |
Из Строительство Wythoff есть десять гиперболических однородные мозаики который может быть основан на правильной восьмиугольной мозаике.
Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, получается 10 форм.
| Равномерная восьмиугольная / треугольная мозаика | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [8,3], (*832) | [8,3]+ (832) | [1+,8,3] (*443) | [8,3+] (3*4) | ||||||||||
| {8,3} | т {8,3} | г {8,3} | т {3,8} | {3,8} | рр {8,3} s2{3,8} | tr {8,3} | ср {8,3} | ч {8,3} | час2{8,3} | с {3,8} | |||
| Униформа двойников | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V (3,4)3 | V8.6.6 | V35.4 | |||
| Равномерная восьмиугольная / квадратная мозаика | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [8,4], (*842) (с подсимметрией [8,8] (* 882), [(4,4,4)] (* 444), [∞, 4, ∞] (* 4222) индекса 2) (И [(∞, 4, ∞, 4)] (* 4242) подсимметрия индекса 4) | |||||||||||
= = = | = | = = = | = | = = | = | ||||||
 |  |  |  |  |  |  | |||||
| {8,4} | т {8,4} | г {8,4} | 2t {8,4} = t {4,8} | 2r {8,4} = {4,8} | рр {8,4} | tr {8,4} | |||||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  | |||||
| V84 | V4.16.16 | V (4,8)2 | V8.8.8 | V48 | V4.4.4.8 | V4.8.16 | |||||
| Чередования | |||||||||||
| [1+,8,4] (*444) | [8+,4] (8*2) | [8,1+,4] (*4222) | [8,4+] (4*4) | [8,4,1+] (*882) | [(8,4,2+)] (2*42) | [8,4]+ (842) | |||||
= | = | = | = | = | = | ||||||
 |  |  |  |  |  |  | |||||
| ч {8,4} | с {8,4} | ч. {8,4} | с {4,8} | ч {4,8} | чрр {8,4} | sr {8,4} | |||||
| Двойное чередование | |||||||||||
 |  |  |  |  | |||||||
| V (4,4)4 | V3. (3.8)2 | V (4.4.4)2 | V (3,4)3 | V88 | V4.44 | V3.3.4.3.8 | |||||
| Равномерные (4,4,4) мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,4,4)], (*444) | [(4,4,4)]+ (444) | [(1+,4,4,4)] (*4242) | [(4+,4,4)] (4*22) | ||||||||
 |  |  |  |  |  |  |  |  |  | ||
| т0(4,4,4) ч {8,4} | т0,1(4,4,4) час2{8,4} | т1(4,4,4) {4,8}1/2 | т1,2(4,4,4) час2{8,4} | т2(4,4,4) ч {8,4} | т0,2(4,4,4) г {4,8}1/2 | т0,1,2(4,4,4) т {4,8}1/2 | с (4,4,4) с {4,8}1/2 | ч (4,4,4) ч {4,8}1/2 | час (4,4,4) ч. {4,8}1/2 | ||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  |  |  |  | ||
| V (4,4)4 | V4.8.4.8 | V (4,4)4 | V4.8.4.8 | V (4,4)4 | V4.8.4.8 | V8.8.8 | V3.4.3.4.3.4 | V88 | V (4,4)3 | ||
Смотрите также
| Викискладе есть медиафайлы по теме Восьмиугольная черепица Order-3. |
- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.

