WikiDer > Апейрогональная мозаика порядка 4
Эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к сделать понятным для неспециалистов, не снимая технических деталей. (Июль 2013) (Узнайте, как и когда удалить этот шаблон сообщения) |
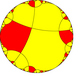
| Апейрогональная мозаика порядка 4 | |
|---|---|
 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболический правильный тайлинг |
| Конфигурация вершины | ∞4 |
| Символ Шлефли | {∞,4} г {∞, ∞} t (∞, ∞, ∞) т0,1,2,3(∞,∞,∞,∞) |
| Символ Wythoff | 4 | ∞ 2 2 | ∞ ∞ ∞ ∞ | ∞ |
| Диаграмма Кокстера | |
| Группа симметрии | [∞,4], (*∞42) [∞,∞], (*∞∞2) [(∞,∞,∞)], (*∞∞∞) (*∞∞∞∞) |
| Двойной | Квадратная мозаика бесконечного порядка |
| Характеристики | Вершинно-транзитивный, ребро-транзитивный, лицо переходный ребро-транзитивный |
В геометрия, то апейрогональная мозаика порядка 4 это обычный черепица из гиперболическая плоскость. Она имеет Символ Шлефли из {∞, 4}.
Симметрия
Эта мозаика представляет собой зеркальные линии * 2∞ симметрия. Двойственный к этому замощению представляет фундаментальные области орбифолдная запись Симметрия * ∞∞∞∞, квадратная область с четырьмя идеальными вершинами.
Равномерная окраска
Как евклидова квадратная черепица Для этого тайлинга существует 9 однородных раскрасок, причем 3 равномерных раскраски создаются треугольными отражающими областями. Четвертый может быть построен из бесконечной квадратной симметрии (* ∞∞∞∞) с 4-мя цветами вокруг вершины. В шахматная доска, r {∞, ∞}, раскраска определяет фундаментальные области симметрии [(∞, 4,4)], (* ∞44), обычно показываемые как черные и белые области отражающих ориентаций.
Связанные многогранники и мозаика
Эта мозаика также топологически связана как часть последовательности правильных многогранников и мозаик с четырьмя гранями на вершину, начиная с октаэдр, с Символ Шлефли {n, 4} и диаграмма Кокстера ![]()
![]()
![]()
![]()
![]() , при этом n стремится к бесконечности.
, при этом n стремится к бесконечности.
| *п42 мутации симметрии правильных мозаик: {п,4} | |||||||
|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Гиперболические мозаики | |||||
 |  |  |  |  |  |  | |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
| Паракомпактные равномерные мозаики в семействе [∞, 4] | |||||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  | |
| {∞,4} | т {∞, 4} | г {∞, 4} | 2t {∞, 4} = t {4, ∞} | 2r {∞, 4} = {4, ∞} | rr {∞, 4} | tr {∞, 4} | |
| Двойные цифры | |||||||
 |  |  |  |  |  |  | |
| V∞4 | V4.∞.∞ | V (4.∞)2 | V8.8.∞ | V4∞ | V43.∞ | V4.8.∞ | |
| Чередования | |||||||
| [1+,∞,4] (*44∞) | [∞+,4] (∞*2) | [∞,1+,4] (*2∞2∞) | [∞,4+] (4*∞) | [∞,4,1+] (*∞∞2) | [(∞,4,2+)] (2*2∞) | [∞,4]+ (∞42) | |
= | = | ||||||
| h {∞, 4} | s {∞, 4} | ч {∞, 4} | s {4, ∞} | h {4, ∞} | чрр {∞, 4} | s {∞, 4} | |
 |  |  |  | ||||
| Двойное чередование | |||||||
 |  | ||||||
| V (∞.4)4 | V3. (3.∞)2 | V (4.∞.4)2 | V3.∞. (3.4)2 | V∞∞ | V∞.44 | V3.3.4.3.∞ | |
| Паракомпактные равномерные мозаики в семействе [∞, ∞] | ||||||
|---|---|---|---|---|---|---|
= = | = = | = = | = = | = = | = | = |
 |  |  |  |  |  |  |
| {∞,∞} | т {∞, ∞} | г {∞, ∞} | 2t {∞, ∞} = t {∞, ∞} | 2r {∞, ∞} = {∞, ∞} | rr {∞, ∞} | tr {∞, ∞} |
| Двойные мозаики | ||||||
 |  |  |  |  |  |  |
| V∞∞ | V∞.∞.∞ | V (∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| Чередования | ||||||
| [1+,∞,∞] (*∞∞2) | [∞+,∞] (∞*∞) | [∞,1+,∞] (*∞∞∞∞) | [∞,∞+] (∞*∞) | [∞,∞,1+] (*∞∞2) | [(∞,∞,2+)] (2*∞∞) | [∞,∞]+ (2∞∞) |
 |  |  |  |  |  | |
| h {∞, ∞} | s {∞, ∞} | hr {∞, ∞} | s {∞, ∞} | час2{∞,∞} | чрр {∞, ∞} | sr {∞, ∞} |
| Двойное чередование | ||||||
 |  |  |  | |||
| V (∞.∞)∞ | V (3.∞)3 | V (∞.4)4 | V (3.∞)3 | V∞∞ | V (4.∞.4)2 | V3.3.∞.3.∞ |
| Паракомпактные равномерные мозаики в семействе [(∞, ∞, ∞)] | ||||||
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
| (∞,∞,∞) h {∞, ∞} | г (∞, ∞, ∞) час2{∞,∞} | (∞,∞,∞) h {∞, ∞} | г (∞, ∞, ∞) час2{∞,∞} | (∞,∞,∞) h {∞, ∞} | г (∞, ∞, ∞) г {∞, ∞} | t (∞, ∞, ∞) т {∞, ∞} |
| Двойные мозаики | ||||||
 |  |  |  |  |  |  |
| V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞.∞.∞ |
| Чередования | ||||||
| [(1+,∞,∞,∞)] (*∞∞∞∞) | [∞+,∞,∞)] (∞*∞) | [∞,1+,∞,∞)] (*∞∞∞∞) | [∞,∞+,∞)] (∞*∞) | [(∞,∞,∞,1+)] (*∞∞∞∞) | [(∞,∞,∞+)] (∞*∞) | [∞,∞,∞)]+ (∞∞∞) |
 |  |  |  |  |  |  |
| Двойное чередование | ||||||
 |  |  |  |  |  | |
| V (∞.∞)∞ | V (∞.4)4 | V (∞.∞)∞ | V (∞.4)4 | V (∞.∞)∞ | V (∞.4)4 | V3.∞.3.∞.3.∞ |
Смотрите также
| Викискладе есть медиафайлы по теме Апейрогональная мозаика порядка 4. |
- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.