WikiDer > Усеченная шестиугольная мозаика
| Усеченная шестиугольная мозаика | |
|---|---|
 | |
| Тип | Полурегулярная черепица |
| Конфигурация вершины | 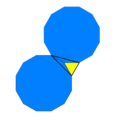 3.12.12 |
| Символ Шлефли | т {6,3} |
| Символ Wythoff | 2 3 | 6 |
| Диаграмма Кокстера |     |
| Симметрия | p6m, [6,3], (*632) |
| Симметрия вращения | p6, [6,3]+, (632) |
| Акроним Bowers | Toxat |
| Двойной | Треугольная черепица Triakis |
| Характеристики | Вершинно-транзитивный |
В геометрия, то усеченная шестиугольная мозаика является полурегулярным замощением Евклидова плоскость. Есть 2 двенадцатиугольники (12 сторон) и один треугольник на каждой вершина.
Как следует из названия, эта мозаика построена усечение операция применяется к шестиугольная черепица, оставляя додекагоны на месте оригинального шестиугольники, и новые треугольники в исходных положениях вершин. Дается расширенный Символ Шлефли из т{6,3}.
Конвей называет это усеченный гексилль, построенный как усечение операция применяется к шестиугольная черепица (гексилль).
Есть 3 обычный и 8 полуправильные мозаики в плоскости.
Равномерная окраска
Здесь только один равномерная окраска усеченной шестиугольной мозаики. (Назовите цвета индексами вокруг вершины: 122.)
Топологически идентичные мозаики
В двенадцатигранный лица могут иметь различную геометрию, например:
 |  |
 |  |
Связанные многогранники и мозаики
Конструкции Wythoff из шестиугольных и треугольных мозаик
Словно равномерные многогранники есть восемь однородные мозаики который может быть основан на правильном шестиугольном тайлинге (или двойственном треугольная черепица).
Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, можно получить 8 форм, 7 из которых топологически различны. (The усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)
| Однородные шестиугольные / треугольные мозаики | ||||||||
|---|---|---|---|---|---|---|---|---|
| Фундаментальный домены | Симметрия: [6,3], (*632) | [6,3]+, (632) | ||||||
| {6,3} | т {6,3} | г {6,3} | т {3,6} | {3,6} | рр {6,3} | tr {6,3} | sr {6,3} | |
| | | | | | |  | |
 |  |  |  |  |  |  |  |  |
| Конфиг. | 63 | 3.12.12 | (6.3)2 | 6.6.6 | 36 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 |
Мутации симметрии
Этот тайлинг топологически связан как часть последовательности равномерных усеченный многогранники с конфигурации вершин (3.2n.2n) и [n, 3] Группа Коксетера симметрия.
| *п32 мутации симметрии усеченных мозаик: t {п,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | ||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | |
| Усеченный цифры |  |  |  |  | |  |  |  |  |  |  |
| Символ | т {2,3} | т {3,3} | т {4,3} | т {5,3} | т {6,3} | т {7,3} | т {8,3} | т {∞, 3} | т {12i, 3} | т {9i, 3} | т {6i, 3} |
| Triakis цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
Связанные 2-однородные мозаики
Два 2-однородные мозаики связаны расчлененными двенадцатиугольники в центральный шестиугольник и 6 окружающих треугольников и квадратов.[1][2]
| 1-униформа | Рассечение | 2-равномерные рассечения | |
|---|---|---|---|
(3.122) |  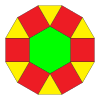 |  (3.4.6.4) & (33.42) |  (3.4.6.4) & (32.4.3.4) |
| Двойные мозаики | |||
 V3.122 | .png)
|  V3.4.6.4 и V33.42 |  V3.4.6.4 и V32.4.3.4 |
Упаковка круга
Усеченная шестиугольная мозаика может использоваться как упаковка круга, поместив круги равного диаметра в центре каждой точки.[3] Каждый круг находится в контакте с 3 другими кругами в упаковке (номер поцелуя). Это упаковка с самой низкой плотностью, которую можно создать из однородной плитки.
Треугольная черепица Triakis
| Треугольная черепица Triakis | |
|---|---|
| |
| Тип | Двойной полурегулярный тайлинг |
| Лица | треугольник |
| Диаграмма Кокстера |  |
| Группа симметрии | p6m, [6,3], (* 632) |
| Группа вращения | p6, [6,3]+, (632) |
| Двойной многогранник | Усеченная шестиугольная мозаика |
| Конфигурация лица | V3.12.12 |
| Характеристики | лицо переходный |
В треугольная плитка Triakis является замощением евклидовой плоскости. Это равносторонний треугольная черепица с каждым треугольником, разделенным на три тупых треугольника (углы 30-30-120) от центральной точки. Он помечен конфигурация лица V3.12.12, потому что каждая грань равнобедренного треугольника имеет два типа вершин: одну с 3 треугольниками и две с 12 треугольниками.
Конвей называет это кисельтиль,[4] построенный как поцелуй операция применяется к треугольная черепица (дельтиль).
В Японии узор называется Асаноха за конопляный лист, хотя это название также применимо к другим формам триаки, таким как триакис икосаэдр и триакис октаэдр.[5]
Это двойная мозаика усеченной шестиугольной мозаики, которая имеет один треугольник и два додекагона в каждой вершине.[6]
Это один из восьми тесселяция краев, мозаики, создаваемые отражениями от каждого края прототипа.[7]
Связанные двойники к однородным мозаикам
Это одна из 7 двойственных однородных мозаик гексагональной симметрии, включая правильные двойственные.
| Симметрия: [6,3], (*632) | [6,3]+, (632) | |||||
|---|---|---|---|---|---|---|
| |  | |  | |  |
| V63 | V3.122 | В (3,6)2 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 |
Смотрите также
 | Викискладе есть медиафайлы по теме Равномерная черепица 3-12-12. |
Рекомендации
- ^ Чави, Д. (1989). "Тайлинги правильными многоугольниками - II: Каталог мозаик". Компьютеры и математика с приложениями. 17: 147–165. Дои:10.1016/0898-1221(89)90156-9.CS1 maint: ref = harv (связь)
- ^ «Архивная копия». Архивировано из оригинал на 2009-09-09. Получено 2006-09-09.CS1 maint: заархивированная копия как заголовок (связь)
- ^ Порядок в космосе: справочник по дизайну, Кейт Кричлоу, стр.74-75, шаблон G
- ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 «Архивная копия». Архивировано из оригинал в 2010-09-19. Получено 2012-01-20.CS1 maint: заархивированная копия как заголовок (связь) (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, таблица с. 288)
- ^ Иносе, Микио. "mikworks.com: Оригинальная работа: Асаноха". www.mikworks.com. Получено 20 апреля 2018.
- ^ Вайсштейн, Эрик В. «Двойная тесселяция». MathWorld.
- ^ Кирби, Мэтью; Умбле, Рональд (2011), «Тесселяция краев и головоломки со складыванием штампов», Математический журнал, 84 (4): 283–289, arXiv:0908.3257, Дои:10.4169 / math.mag.84.4.283, МИСТЕР 2843659.
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]
- Грюнбаум, Бранко И Шепард, Г.С. (1987). Плитки и узоры. Нью-Йорк: У. Х. Фриман. ISBN 0-7167-1193-1. (Глава 2.1: Регулярные и однородные мозаики, п. 58-65)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. стр. 39. ISBN 0-486-23729-X.
- Кит Кричлоу, Заказ в космосе: справочник по дизайну, 1970, с. 69-61, узор E, двойной стр. 77-76, узор 1
- Дейл Сеймур и Джилл Бриттон, Введение в мозаику, 1989, ISBN 978-0866514613, pp. 50–56, dual p. 117
внешняя ссылка
- Вайсштейн, Эрик В. «Полурегулярная тесселяция». MathWorld.
- Клитцинг, Ричард. "2D евклидовы мозаики o3x6x - toxat - O7".
