WikiDer > Список изотоксальных многогранников и мозаик - Википедия
В геометрия, изотоксальный многогранники и мозаики определяются тем свойством, что они обладают симметрией, соединяющей любое ребро с любым другим ребром.[1] Многогранники с этим свойством также можно назвать реберно-транзитивными, но их следует отличать от реберно-транзитивные графы, где симметрии комбинаторные, а не геометрические.
Правильные многогранники являются изоэдральными (гранно-транзитивными), изогональными (вершинно-транзитивными) и изотоксальными (реберно-транзитивными).
Квазирегулярный многогранники изогональны и изотоксальны, но не изоэдральны; их двойники изоэдральны и изотоксальны, но не изогональны.
Двойник изотоксального многогранника также является изотоксальным многогранником. (См. Двойной многогранник статья.)
Выпуклые изотоксальные многогранники
Двойник выпуклого многогранника также является выпуклым многогранником.[2]
Есть девять выпуклый изотоксальные многогранники на основе Платоновы тела: пять (правильных) Платоновых тел, два (квазирегулярный) общие ядра двойственных Платоновых тел и их два двойственных.
В фигуры вершин квазирегулярными формами являются (квадраты или) прямоугольники; фигурами вершин двойников квазирегулярных форм являются (равносторонние треугольники и равносторонние треугольники, или) равносторонние треугольники и квадраты, или равносторонние треугольники и правильные пятиугольники.
| Форма | Обычный | Двойной обычный | Квазирегулярный | Квазирегулярный дуальный |
|---|---|---|---|---|
| Символ Wythoff | q | 2 шт. | p | 2 кв. | 2 | p q | |
| Конфигурация вершины | пq | qп | p.q.p.q | |
| р = 3 q = 3 |  Тетраэдр {3,3} 3 | 2 3 |  Тетраэдр {3,3} 3 | 2 3 |  Тетратетраэдр (Октаэдр) 2 | 3 3 |  Куб (Ромбический шестигранник) |
| р = 4 q = 3 |  Куб {4,3} 3 | 2 4 |  Октаэдр {3,4} 4 | 2 3 |  Кубооктаэдр 2 | 3 4 |  Ромбический додекаэдр |
| р = 5 q = 3 |  Додекаэдр {5,3} 3 | 2 5 |  Икосаэдр {3,5} 5 | 2 3 |  Икосододекаэдр 2 | 3 5 |  Ромбический триаконтаэдр |
Изотоксальные звездчатые многогранники
Двойник невыпуклого многогранника также является невыпуклым многогранником.[2] (По контрасту.)
Существует десять невыпуклых изотоксальных многогранников, основанных на квазирегулярный октаэдр, кубооктаэдр и икосододекаэдр: пять (квазирегулярные) гемиполиэдры на основе квазирегулярного октаэдра, кубооктаэдра и икосододекаэдра и их пяти (бесконечных) двойников:
| Форма | Квазирегулярный | Квазирегулярный дуальный |
|---|---|---|
| p = q = |   Тетрагемигексаэдр |  Тетрагемигексакрон |
| p = q = |   Кубогемиоктаэдр |  Гексагемиоктакрон |
  Октагемиоктаэдр |  Октахемиоктакрон (визуально неотличимы от гексагемиоктакрона) (*) | |
| p = q = |   Малый икосигемидодекаэдр |  Икосихемидодекакрон малый (визуально неотличимы от малого додекагемидодекакрона) (*) |
  Малый додекагемидодекаэдр |  Малый додекагемидодекакрон |
(*) Грани, ребра и точки пересечения совпадают; только некоторые другие из этих точек пересечения, не находящиеся на бесконечности, считаются вершинами.
Имеется шестнадцать невыпуклых изотоксальных многогранников, основанных на Многогранники Кеплера – Пуансо: четыре (правильных) многогранника Кеплера – Пуансо, шесть (квазирегулярный) общие ядра двойных многогранников Кеплера – Пуансо (включая четыре гемиполиэдра) и их шесть двойных (включая четыре (бесконечных) двойных гемиполиэдра):
| Форма | Обычный | Двойной обычный | Квазирегулярный | Квазирегулярный дуальный |
|---|---|---|---|---|
| Символ Wythoff | q | 2 шт. | p | 2 кв. | 2 | p q | |
| Конфигурация вершины | пq | qп | p.q.p.q | |
| р = 5/2 q = 3 |   Большой звездчатый додекаэдр {5/2,3}
|   Большой икосаэдр {3,5/2}
|   Большой икосододекаэдр 2 | 3 5/2 |  Большой ромбический триаконтаэдр |
  Большой икосигемидодекаэдр |  Большой икосихемидодекакрон | |||
  Большой додекагемидодекаэдр |  Большой додекагемидодекакрон | |||
| р = 5/2 q = 5 |   Малый звездчатый додекаэдр {5/2,5}
|   Большой додекаэдр {5,5/2}
|   Додекадодекаэдр 2 | 5 5/2 |  Медиальный ромбический триаконтаэдр |
  Малый икосигемидодекаэдр |  Малый додекагемикосакрон | |||
  Большой додекагемидодекаэдр |  Великий додекагемикосакрон |
Наконец, есть шесть других невыпуклых изотоксальных многогранников: три квазирегулярных дитригональных (3 | p q) звездчатых многогранника и их три двойных:
| Квазирегулярный | Квазирегулярный дуальный |
|---|---|
| 3 | p q | |
  Большой дитригональный икосододекаэдр 3/2 | 3 5 |  Большой триамбический икосаэдр |
  Дитригональный додекадодекаэдр 3 | 5/3 5 |  Медиальный триамбический икосаэдр |
  Малый дитригональный икосододекаэдр 3 | 5/2 3 |  Малый триамбический икосаэдр |
Изотоксальные мозаики евклидовой плоскости
Есть по крайней мере 5 многоугольных мозаик евклидовой плоскости, которые являются изотоксальными. (Самодуальный квадратная черепица воссоздает себя во всех четырех формах.)
| Обычный | Двойной обычный | Квазирегулярный | Квазирегулярный дуальный |
|---|---|---|---|
 Шестиугольная черепица {6,3} 6 | 2 3 |  Треугольная черепица {3,6} 3 | 2 3 |  Трехгранная черепица 2 | 3 6 |  Ромбильная плитка |
 Квадратная плитка {4,4} 4 | 2 4 |  Квадратная плитка {4,4} 2 | 4 4 |  Квадратная плитка {4,4} 4 | 2 4 |  Квадратная плитка {4,4} |
Изотоксальные мозаики гиперболической плоскости
Существует бесконечно много изотоксальных многоугольных мозаик гиперболической плоскости, включая конструкции Витхоффа из регулярные гиперболические мозаики {p, q} и неправые (p q r) группы.
Вот шесть (p q 2) семейств, каждое с двумя регулярными формами и одной квазирегулярной формой. У всех есть ромбические двойники квазирегулярной формы, но показан только один:
| [p, q] | {p, q} | {q, p} | г {р, д} | Двойной r {p, q} |
|---|---|---|---|---|
| Кокстер-Дынкин | ||||
| [7,3] |  {7,3} |  {3,7} |  г {7,3} | 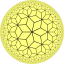 |
| [8,3] |  {8,3} |  {3,8} |  г {8,3} |  |
| [5,4] |  {5,4} |  {4,5} |  г {5,4} |  |
| [6,4] |  {6,4} |  {4,6} |  г {6,4} |  |
| [8,4] |  {8,4} |  {4,8} |  г {8,3} |  |
| [5,5] |  {5,5} |  {5,5} |  г {5,5} |  |
Вот 3 примера (p q r) семейства, каждое с 3 квазирегулярными формами. Двойники не показаны, но имеют изотоксальные шестиугольные и восьмиугольные грани.
| Кокстер-Дынкин | |||
|---|---|---|---|
| (4 3 3) |  3 | 4 3 |  3 | 4 3 |  4 | 3 3 |
| (4 4 3) |  4 | 4 3 |  3 | 4 4 |  4 | 4 3 |
| (4 4 4) |  4 | 4 4 |  4 | 4 4 |  4 | 4 4 |
Изотоксальные мозаики сферы
Все перечисленные выше изотоксальные многогранники могут быть построены как изотоксальные мозаики сферы.
Помимо сферических мозаик, есть еще два семейства, которые вырождены как многогранники. Даже заказанный осоэдр можно полуправильный, чередуя два луна, и таким образом изотоксический:
Рекомендации
- ^ Питер Р. Кромвель, Многогранники, Издательство Кембриджского университета 1997, ISBN 0-521-55432-2, п. 371
- ^ а б "двойственность". maths.ac-noumea.nc. Получено 2020-10-01.
- Грюнбаум, Бранко; Шепард, Г. К. (1987). Плитки и узоры. Нью-Йорк: У. Х. Фриман. ISBN 0-7167-1193-1. (6.4 Изотоксальные плитки, 309–321)
- Коксетер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 246 (916): 401–450, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446, S2CID 202575183

