WikiDer > Платоново твердое тело
В трехмерное пространство, а Платоново твердое тело это обычный, выпуклый многогранник. Он построен конгруэнтный (идентичны по форме и размеру), обычный (все углы равны и все стороны равны), многоугольный лица с одинаковым количеством лиц, встречающихся на каждом вершина. Этим критериям соответствуют пять твердых тел:
| Тетраэдр | Куб | Октаэдр | Додекаэдр | Икосаэдр |
| Четыре лица | Шесть лиц | Восемь лиц | Двенадцать лиц | Двадцать лиц |
 |  |  |  |  |
Геометры изучали Платоновы тела на протяжении тысяч лет.[1] Они названы в честь древнегреческий философ Платон который выдвинул гипотезу в одном из своих диалогов, Тимей, что классические элементы были сделаны из этих твердых тел.[2]
История
Платоновы тела были известны с древних времен.резные каменные шары созданный поздний неолит люди из Шотландия представляют эти формы; однако эти шары имеют округлые выступы, а не являются многогранными, количество выступов часто отличается от количества вершин Платоновых тел, нет шара, выступы которого соответствуют 20 вершинам додекаэдра, и расположение выступов не соответствует всегда симметричный.[3]
В древние греки широко изучал Платоновы тела. Некоторые источники (например, Прокл) кредит Пифагор с их открытием. Другие данные свидетельствуют о том, что он мог быть знаком только с тетраэдром, кубом и додекаэдром, и что открытие октаэдра и икосаэдра принадлежит Theaetetus, современник Платона. В любом случае, Теэтет дал математическое описание всех пяти и, возможно, был ответственным за первое известное доказательство того, что никаких других выпуклых правильных многогранников не существует.
Платоновы тела занимают видное место в философии Платон, их тезка. Платон писал о них в диалоге Тимей c.360 г. до н. Э. в котором он связал каждого из четырех классические элементы (земной шар, воздуха, воды, и Огонь) с обычным телом. Земля ассоциировалась с кубом, воздух - с октаэдром, вода - с икосаэдром, а огонь - с тетраэдром. У этих ассоциаций было интуитивное обоснование: жар огня ощущается острым и колющим (как маленькие тетраэдры). Воздух состоит из октаэдра; его крохотные компоненты настолько гладкие, что это почти не чувствуется. Вода, икосаэдр, вытекает из руки, когда ее поднимают, как будто она состоит из крошечных шариков. Напротив, шестигранник (куб) представляет собой очень несферическое твердое тело, представляющее «землю». Эти неуклюжие маленькие твердые частицы заставляют грязь крошиться и ломаться, когда их собирают в резком отличие от плавного потока воды.[нужна цитата] Более того, куб - единственное правильное твердое тело, которое мозаика Евклидово пространство считалось причиной прочности Земли.
О пятом платоновом теле, додекаэдре, Платон неявно заметил: «... бог использовал [его] для расстановки созвездий на всем небе». Аристотель добавил пятый элемент, айтер (эфир по-латыни, «эфир» по-английски) и постулировал, что небеса сделаны из этого элемента, но он не был заинтересован в сопоставлении его с пятым телом Платона.[4]
Евклид полностью математически описал Платоновы тела в Элементы, последняя книга (Книга XIII) которой посвящена их свойствам. В предложениях 13–17 Книги XIII описывается построение тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в таком порядке. Для каждого твердого тела Евклид находит отношение диаметра описанной сферы к длине края. В предложении 18 он утверждает, что выпуклых правильных многогранников больше не существует.Андреас Шпайзер отстаивал точку зрения, согласно которой построение 5 правильных тел является главной целью дедуктивной системы, канонизированной в Элементы.[5] Большая часть информации в Книге XIII, вероятно, взята из работ Теэтета.
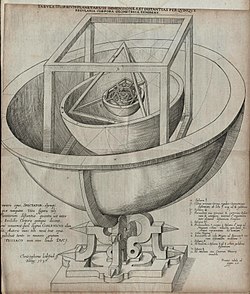
В 16 веке немецкая астроном Иоганн Кеплер пытался связать пять внеземных планеты известно в то время о пяти Платоновых телах. В Mysterium Cosmographicum, опубликованной в 1596 г., Кеплер предложил модель Солнечная система в котором пять твердых тел были помещены друг в друга и разделены серией вписанных и описанных сфер. Кеплер предположил, что отношения расстояний между шестью планетами, известными в то время, можно понять в терминах пяти Платоновых тел, заключенных в сферу, которая представляет собой орбиту Сатурн. Каждая из шести сфер соответствовала одной из планет (Меркурий, Венера, земной шар, Марс, Юпитер, и Сатурн). Твердые тела были упорядочены: самым внутренним из них был октаэдр, за ним следовали икосаэдр, додекаэдр, тетраэдр и, наконец, куб, тем самым определяя структуру Солнечной системы и отношения расстояний между планетами Платоновыми телами. В конце концов, от первоначальной идеи Кеплера пришлось отказаться, но из его исследований пришла его идея. три закона орбитальной динамики, первым из которых был орбиты планет - эллипсы вместо кружков, меняя курс физики и астрономии. Он также обнаружил Твердые тела Кеплера.
Декартовы координаты
Для Платоновых тел с центром в начале координат простой Декартовы координаты вершин приведены ниже. Греческая буква φ используется для представления Золотое сечение 1 + √5/2 ≈ 1.6180.
Координаты тетраэдра, додекаэдра и икосаэдра даны в двух наборах ориентации, каждый из которых содержит половина знаковой и позиционной перестановки координат.
Эти координаты показывают определенные отношения между Платоновыми телами: вершины тетраэдра представляют половину вершин куба, как {4,3} или ![]()
![]()
![]()
![]()
![]() , один из двух наборов по 4 вершины в двойных позициях, как h {4,3} или
, один из двух наборов по 4 вершины в двойных позициях, как h {4,3} или ![]()
![]()
![]()
![]()
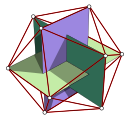
![]() . Обе тетраэдрические позиции делают соединение звездчатый октаэдр.
. Обе тетраэдрические позиции делают соединение звездчатый октаэдр.
Координаты икосаэдра связаны с двумя чередующимися наборами координат неоднородного усеченный октаэдр, t {3,4} или ![]()
![]()
![]()
![]()
![]() , также называемый курносый октаэдр, как s {3,4} или
, также называемый курносый октаэдр, как s {3,4} или ![]()
![]()
![]()
![]()
![]() , и видели в соединение двух икосаэдров.
, и видели в соединение двух икосаэдров.
Восемь вершин додекаэдра являются общими с кубом. Завершение всех ориентаций приводит к соединение пяти кубиков.
Комбинаторные свойства
Выпуклый многогранник является платоновым телом тогда и только тогда, когда
- все его лица конгруэнтный выпуклый правильные многоугольники,
- ни одна из его граней не пересекается, кроме как по краям, и
- одинаковое количество лиц встречается на каждом из вершины.
Следовательно, каждое платоново твердое тело можно обозначить символом {п, q} куда
- п - количество ребер (или, что то же самое, вершин) каждой грани, и
- q это количество граней (или, что то же самое, ребер), которые пересекаются в каждой вершине.
Символ {п, q}, называется Символ Шлефли, дает комбинаторный описание многогранника. Символы Шлефли пяти Платоновых тел приведены в таблице ниже.
| Многогранник | Вершины | Края | Лица | Символ Шлефли | Конфигурация вершины | |
|---|---|---|---|---|---|---|
| тетраэдр | 4 | 6 | 4 | {3, 3} | 3.3.3 | |
| куб |  | 8 | 12 | 6 | {4, 3} | 4.4.4 |
| октаэдр |  | 6 | 12 | 8 | {3, 4} | 3.3.3.3 |
| додекаэдр |  | 20 | 30 | 12 | {5, 3} | 5.5.5 |
| икосаэдр | 12 | 30 | 20 | {3, 5} | 3.3.3.3.3 | |
Вся прочая комбинаторная информация об этих телах, такая как общее количество вершин (V), ребра (E), а лица (F), можно определить из п и q. Поскольку любое ребро соединяет две вершины и имеет две смежные грани, мы должны иметь:
Другое соотношение между этими значениями дается выражением Формула Эйлера:
Это можно доказать разными способами. Вместе эти три отношения полностью определяют V, E, и F:
Обмен п и q развязки F и V при выходе E без изменений. Геометрическую интерпретацию этого свойства см. В § Двойные многогранники ниже.
Как конфигурация
Элементы многогранника можно выразить через матрица конфигурации. Строки и столбцы соответствуют вершинам, ребрам и граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем многограннике. Недиагональные числа говорят, сколько элементов столбца находится в элементе строки или рядом с ним. Матрицы конфигурации двойных пар многогранников повернуты на 180 градусов друг от друга.[6]
| {p, q} | Платонические конфигурации | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| групповой заказ: грамм = 8pq/(4-(п-2)(q-2)) | грамм=24 | грамм=48 | грамм=120 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Классификация
Классический результат состоит в том, что существует только пять выпуклых правильных многогранников. Два общих аргумента, приведенные ниже, демонстрируют, что может существовать не более пяти Платоновых тел, но положительная демонстрация существования любого данного твердого тела - это отдельный вопрос, который требует явного построения.
Геометрическое доказательство
{3,3} Дефект 180 ° |  {3,4} Дефект 120 ° |  {3,5} Дефект 60 ° |  {3,6} Дефект 0 ° |
 {4,3} Дефект 90 ° |  {4,4} Дефект 0 ° |  {5,3} Дефект 36 ° |  {6,3} Дефект 0 ° |
| Вершина требует не менее 3 граней и угловой дефект. Угловой дефект 0 ° заполнит евклидову плоскость правильной мозаикой. К Теорема Декарта, количество вершин 720 ° /дефект. | |||
Следующий геометрический аргумент очень похож на тот, который дает Евклид в Элементы:
- Каждая вершина тела должна быть вершиной как минимум для трех граней.
- В каждой вершине твердого тела сумма между смежными гранями углов между их соответствующими смежными сторонами должна быть меньше 360 °. Величина меньше 360 ° называется угловой дефект.
- Углы при всех вершинах всех граней Платонового тела идентичны: каждая вершина каждой грани должна давать меньше, чем 360°/3 = 120°.
- Правильные многоугольники шесть или более сторон имеют углы только 120 ° или более, поэтому общая грань должна быть треугольником, квадратом или пятиугольником. Для этих разных форм лиц выполняется следующее:
- Треугольный грани: каждая вершина правильного треугольника равна 60 °, поэтому фигура может иметь 3, 4 или 5 треугольников, пересекающихся в вершине; это тетраэдр, октаэдр и икосаэдр соответственно.
- Квадрат грани: каждая вершина квадрата равна 90 °, поэтому возможна только одна компоновка с тремя гранями в вершине - куб.
- Пятиугольный грани: каждая вершина 108 °; опять же, возможно только одно расположение трех граней в вершине - додекаэдр.
- Всего это дает 5 возможных Платоновых тел.
Топологическое доказательство
Чисто топологический доказательство можно сделать, используя только комбинаторную информацию о телах. Ключ Наблюдение Эйлера который V − E + F = 2 и тот факт, что ПФ = 2E = qV, куда п обозначает количество ребер каждой грани и q для количества ребер, пересекающихся в каждой вершине. Комбинируя эти уравнения, получаем уравнение
Тогда простая алгебраическая манипуляция дает
С E строго положительно, мы должны иметь
Используя тот факт, что п и q оба должны быть не менее 3, легко увидеть, что существует только пять возможностей для {п, q}:
- {3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}.
Геометрические свойства
Углы
Есть ряд углы связаны с каждым Платоновым телом. В двугранный угол - внутренний угол между любыми двумя плоскостями граней. Двугранный угол, θ, твердого {п,q} дается формулой
Иногда это удобнее выразить в терминах касательная к
Количество час (называется Число Кокстера) равно 4, 6, 6, 10 и 10 для тетраэдра, куба, октаэдра, додекаэдра и икосаэдра соответственно.
В угловой дефицит в вершине многогранника - это разница между суммой углов граней в этой вершине и 2π. Дефект, δ, в любой вершине Платоновых тел {п,q} является
По теореме Декарта это равно 4π деленное на количество вершин (т.е. общий дефект во всех вершинах равен 4π).
Трехмерным аналогом плоского угла является телесный угол. Телесный угол, Ω, в вершине платонового тела определяется двугранным углом как
Это следует из сферический избыток формула для сферический многоугольник и тот факт, что вершина фигуры многогранника {п,q} является обычным q-гон.
Телесный угол грани, вытянутой из центра платонического тела, равен телесному углу полной сферы (4π стерадианы), разделенные на количество граней. Это равносильно угловому недостатку его дуала.
Различные углы, связанные с Платоновыми телами, представлены в таблице ниже. Числовые значения телесных углов приведены в стерадианы. Постоянная φ = 1 + √5/2 это Золотое сечение.
| Многогранник | Двугранный угол (θ) | загарθ/2 | Дефект (δ) | Вершина телесный угол (Ω) | Лицо телесный угол |
|---|---|---|---|---|---|
| тетраэдр | 70.53° | ||||
| куб | 90° | ||||
| октаэдр | 109.47° | ||||
| додекаэдр | 116.57° | ||||
| икосаэдр | 138.19° |
Радиусы, площадь и объем
Еще одно достоинство регулярности состоит в том, что все Платоновы тела обладают тремя концентрическими сферами:
- то ограниченная сфера который проходит через все вершины,
- то средняя сфера который касается каждого ребра в середине ребра, и
- то вписанная сфера это касается каждой грани в центре грани.
В радиусы из этих сфер называют по окружности, то средний радиус, а inradius. Это расстояния от центра многогранника до вершин, середин ребер и центров граней соответственно. Окружной радиус р и радиус р твердого {п, q} с длиной кромки а даны
куда θ - двугранный угол. Средний радиус ρ дан кем-то
куда час - величина, использованная выше при определении двугранного угла (час = 4, 6, 6, 10 или 10). Отношение окружного радиуса к внутреннему радиусу симметрично в п и q:
В площадь поверхности, А, платонового тела {п, q} легко вычисляется как площадь регулярного п-угольник умноженный на количество граней F. Это:
В объем вычисляется как F раз объем пирамида чья база является регулярным п-угольник, высота которого равна внутреннему радиусу р. То есть,
В следующей таблице перечислены различные радиусы Платоновых тел, а также их площадь поверхности и объем. Общий размер фиксируется по длине кромки, а, чтобы быть равным 2.
| Многогранник (а = 2) | Inradius (р) | Мидрадиус (ρ) | Циркумрадиус (р) | Площадь поверхности (А) | Объем (V) | Объем (края блока) |
|---|---|---|---|---|---|---|
| тетраэдр | ||||||
| куб | ||||||
| октаэдр | ||||||
| додекаэдр | ||||||
| икосаэдр |
Константы φ и ξ в приведенном выше выражении
Среди Платоновых тел додекаэдр или икосаэдр можно рассматривать как лучшее приближение к сфере. Икосаэдр имеет наибольшее количество граней и наибольший двугранный угол, он наиболее плотно обнимает вписанную сферу, а его отношение площади поверхности к объему наиболее близко к таковому у сферы того же размера (то есть либо такой же площади поверхности, либо Тот же объем.) Додекаэдр, с другой стороны, имеет наименьший угловой дефект, наибольший телесный угол при вершине и больше всего заполняет свою описанную сферу.
Точка в пространстве
Для произвольной точки пространства платонового тела с описанным радиусом , расстояние от которого до центроида Платонова тела и его вершины и соответственно, и
- ,
у нас есть[7]
Для всех пяти Платоновых тел мы имеем [7]
Если расстояния от вершины платонового тела в любую точку на его описанной сфере, то [7]
Руперт недвижимость
Многогранник п говорят, что имеет Руперт свойство, если многогранник того же или большего размера и такой же формы, что и п может пройти через дыру в п.[8]Этим свойством обладают все пять Платоновых тел.[8][9][10]
Симметрия
Двойные многогранники
Каждый многогранник имеет двойственный (или «полярный») многогранник со сменой граней и вершин. Двойственное тело каждого Платонова тела является другим Платоновым телом, так что мы можем объединить пять тел в двойные пары.
- Тетраэдр самодвойственный (т.е. его двойник - другой тетраэдр).
- Куб и октаэдр образуют дуальную пару.
- Додекаэдр и икосаэдр образуют двойную пару.
Если многогранник имеет символ Шлефли {п, q}, то его двойник имеет символ {q, п}. В самом деле, каждое комбинаторное свойство одного Платонового тела можно интерпретировать как другое комбинаторное свойство двойственного.
Можно построить двойственный многогранник, взяв его вершины за центры граней исходной фигуры. Соединение центров смежных граней в оригинале образует ребра дуального и, таким образом, меняет местами количество граней и вершин, сохраняя при этом количество ребер.
В более общем смысле, можно дуализовать Платоново твердое тело относительно сферы радиуса d концентрический с твердым телом. Радиусы (р, ρ, р) твердого тела и двойственного к нему (р*, ρ*, р*) связаны
Дуализация по отношению к средней сфере (d = ρ) часто бывает удобно, потому что средняя сфера имеет одинаковое отношение к обоим многогранникам. Принимая d2 = Rr дает двойное твердое тело с одинаковым радиусом описанной окружности и внутренним радиусом (т.е. р* = р и р* = р).
Группы симметрии
В математике понятие симметрия изучается с понятием математическая группа. Каждому многограннику соответствует группа симметрии, представляющий собой набор всех преобразований (Евклидовы изометрии), которые оставляют многогранник инвариантным. В порядок группы симметрии - это число симметрий многогранника. Часто различают полная группа симметрии, который включает размышления, а собственная группа симметрии, который включает только вращения.
Группы симметрии Платоновых тел представляют собой особый класс трехмерные точечные группы известный как многогранные группы. Высокая степень симметрии Платоновых тел можно интерпретировать по-разному. Что наиболее важно, вершины каждого тела эквивалентны относительно действие группы симметрии, а также ребра и грани. Один говорит, что действие группы симметрии переходный на вершинах, ребрах и гранях. Фактически, это еще один способ определения правильности многогранника: многогранник есть обычный если и только если это вершинно-однородный, однотонный, и мундир.
Есть только три группы симметрии, связанные с Платоновыми телами, а не пять, поскольку группа симметрии любого многогранника совпадает с группой симметрии его двойственного. В этом легко убедиться, рассмотрев конструкцию двойственного многогранника. Любая симметрия оригинала должна быть симметрией двойственного и наоборот. Три группы полиэдров:
- то тетраэдрическая группа Т,
- то октаэдрическая группа О (которая также является группой симметрии куба), и
- то группа икосаэдров я (которая также является группой симметрии додекаэдра).
Порядки собственных групп (вращений) равны 12, 24 и 60 соответственно - ровно в два раза больше числа ребер в соответствующих многогранниках. Порядки групп полной симметрии снова вдвое больше (24, 48 и 120). См. (Coxeter 1973) вывод этих фактов. Все Платоновы тела, кроме тетраэдра, являются центрально-симметричный, это означает, что они сохраняются под отражение через начало координат.
В следующей таблице перечислены различные свойства симметрии Платоновых тел. Перечисленные группы симметрии представляют собой полные группы с подгруппами вращения, указанными в скобках (также как и для числа симметрий). Конструкция калейдоскопа Уайтхоффа это метод построения многогранников непосредственно из их групп симметрии. Они перечислены для справки по символу Витхоффа для каждого из Платоновых тел.
| Многогранник | Schläfli символ | Wythoff символ | Двойной многогранник | Группа симметрии (Отражение, вращение) | ||||
|---|---|---|---|---|---|---|---|---|
| Многогранник | Schön. | Кокс. | Сфера. | Заказ | ||||
| тетраэдр | {3, 3} | 3 | 2 3 | тетраэдр | Тетраэдр | Тd Т | [3,3] [3,3]+ | *332 332 | 24 12 |
| куб | {4, 3} | 3 | 2 4 | октаэдр | Восьмигранный | Очас О | [4,3] [4,3]+ | *432 432 | 48 24 |
| октаэдр | {3, 4} | 4 | 2 3 | куб | |||||
| додекаэдр | {5, 3} | 3 | 2 5 | икосаэдр | Икосаэдр | ячас я | [5,3] [5,3]+ | *532 532 | 120 60 |
| икосаэдр | {3, 5} | 5 | 2 3 | додекаэдр | |||||
В природе и технике
Эта секция не цитировать любой источники. (Октябрь 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Тетраэдр, куб и октаэдр встречаются в природе в природе. кристаллические структуры. Этим ни в коем случае не исчерпывается количество возможных форм кристаллов. Однако ни правильный икосаэдр, ни правильный додекаэдр среди них нет. Одна из форм, называемая пиритоэдр (назван в честь группы минералы из которых он типичен) имеет двенадцать пятиугольных граней, расположенных в том же порядке, что и грани правильного додекаэдра. Однако грани пиритоэдра не правильные, поэтому и пиритоэдр не правильный. Аллотропы бора и много соединения бора, Такие как карбид бора, включают дискретные B12 икосаэдры в их кристаллических структурах. Карборановые кислоты также имеют молекулярные структуры, приближенные к правильным икосаэдрам.

В начале 20 века Эрнст Геккель описал (Haeckel, 1904) ряд видов Радиолярии, некоторые из скелетов которых имеют форму различных правильных многогранников. Примеры включают Circoporus octahedrus, Икосаэдры Circogonia, Геометрический литокуб и Circorrhegma dodecahedra. Формы этих существ должны быть очевидны из их названий.
Много вирусы, такой как герпес вируса, имеют форму правильного икосаэдра. Вирусные структуры построены из повторяющихся одинаковых белок субъединицы и икосаэдр - самая простая форма для сборки с использованием этих субъединиц. Используется правильный многогранник, потому что он может быть построен из единственного базового белка, используемого снова и снова; это экономит место в вирусных геном.
В метеорология и климатология, все больший интерес вызывают глобальные численные модели атмосферного потока, использующие геодезические сети основанные на икосаэдре (уточнены триангуляция) вместо более часто используемого долгота/широта сетка. Это дает преимущество равномерно распределенного пространственного разрешения без особенности (т. е. полюсов) за счет несколько большей числовой сложности.
Геометрия космические рамки часто основан на платоновых телах. В системе MERO Платоновы тела используются для обозначения различных конфигураций пространственных фреймов. Например, 1/2O + T относится к конфигурации, состоящей из половины октаэдра и тетраэдра.
Несколько Платоновые углеводороды были синтезированы, в том числе кубан и додекаэдран.
Платоновы тела часто используются для создания игральная кость, потому что кубики такой формы можно сделать справедливый. Шестигранные кости очень распространены, но другие числа обычно используются в ролевые игры. Такие кости обычно обозначают как dп куда п - количество граней (d8, d20 и т. д.); видеть обозначение игральных костей Больше подробностей.
Эти формы часто встречаются в других играх или головоломках. Головоломки похожие на Кубик Рубика бывают всех пяти форм - см. магические многогранники.
Жидкие кристаллы с симметрией платоновых тел
Для промежуточной материальной фазы, называемой жидкие кристаллы, существование таких симметрий было впервые предложено в 1981 г. Х. Кляйнерт и К. Маки.[11][12]В алюминии икосаэдрическая структура была открыта через три года после этого. Дэн Шехтман, что принесло ему Нобелевская премия по химии в 2011.
Связанные многогранники и многогранники
Равномерные многогранники
Существует четыре невыпуклых правильных многогранника, называемых Многогранники Кеплера – Пуансо. Все они имеют икосаэдрическая симметрия и может быть получен как звёздчатые додекаэдра и икосаэдра.
 кубооктаэдр |  икосододекаэдр |
Следующими по правильности выпуклыми многогранниками после Платоновых тел являются многогранники кубооктаэдр, который является исправление куба и октаэдра, а икосододекаэдр, который является выпрямлением додекаэдра и икосаэдра (выпрямление самодуального тетраэдра - правильный октаэдр). Это оба квазирегулярный, что означает, что они однородны по вершинам и ребрам и имеют правильные грани, но не все грани конгруэнтны (попадают в два разных класса). Они составляют двое из тринадцати Архимедовы тела, которые являются выпуклыми равномерные многогранники с многогранной симметрией. Их двойники, ромбический додекаэдр и ромбический триаконтаэдр, являются реберно-гранно-транзитивными, но их грани не правильные, а их вершины бывают двух типов каждая; они двое из тринадцати Каталонские твердые вещества.
Однородные многогранники образуют гораздо более широкий класс многогранников. Эти фигуры однородны по вершинам и имеют один или несколько типов обычный или же звездные многоугольники для лиц. К ним относятся все упомянутые выше многогранники вместе с бесконечным множеством призмы, бесконечный набор антипризмыи 53 другие невыпуклые формы.
В Твердые тела Джонсона - выпуклые многогранники, имеющие правильные грани, но не однородные. Среди них пять из восьми выпуклых дельтаэдры, которые имеют одинаковые правильные грани (все равносторонние треугольники), но не однородны. (Три других выпуклых дельтаэдра - это платоновский тетраэдр, октаэдр и икосаэдр.)
Обычные мозаики
| Платоновы мозаики | ||||
|---|---|---|---|---|
 |  |  |  |  |
| {3,3} | {4,3} | {3,4} | {5,3} | {3,5} |
| Правильные двугранные мозаики | ||||
 |  |  |  |  |
| {2,2} | {3,2} | {4,2} | {5,2} | {6,2}... |
| Правильные госоэдральные мозаики | ||||
 |  |  |  |  |
| {2,2} | {2,3} | {2,4} | {2,5} | {2,6}... |
Три регулярные мозаики плоскости тесно связаны с Платоновыми телами. Действительно, можно рассматривать Платоновы тела как регулярные мозаики сфера. Это делается путем проецирования каждого твердого тела на концентрическую сферу. Лица проецируются на обычные сферические многоугольники которые точно покрывают сферу. Сферические мозаики обеспечивают два бесконечных дополнительных набора регулярных мозаик: Hosohedra, {2,п} с двумя вершинами на полюсах и луна лица, и двойное дигедра, {п, 2} с двумя полусферическими гранями и равномерно расположенными вершинами на экваторе. Такие мозаики были бы вырожденными в истинном трехмерном пространстве как многогранники.
Можно показать, что всякая регулярная мозаика сферы характеризуется парой целых чисел {п, q} с 1/п + 1/q > 1/2. Точно так же регулярная мозаика плоскости характеризуется условием 1/п + 1/q = 1/2. Есть три возможности:
 |  |  |
| {4, 4} | {3, 6} | {6, 3} |
|---|
Аналогичным образом можно рассматривать регулярные мозаики гиперболическая плоскость. Для них характерно состояние 1/п + 1/q < 1/2. Таких мозаик существует бесконечное множество.
 |  |  |  |
| {5, 4} | {4, 5} | {7, 3} | {3, 7} |
|---|
Высшие измерения
В более чем трех измерениях многогранники обобщаются на многогранники, с многомерными выпуклыми правильные многогранники являясь эквивалентами трехмерных Платоновых тел.
В середине 19 века швейцарский математик Людвиг Шлефли открыл четырехмерные аналоги Платоновых тел, названные выпуклые правильные 4-многогранники. Таких фигур ровно шесть; пять аналогичны Платоновым телам 5-элементный как {3,3,3}, 16 ячеек как {3,3,4}, 600 ячеек как {3,3,5}, тессеракт как {4,3,3}, и 120 ячеек как {5,3,3}, а шестой - самодуальный 24-элементный, {3,4,3}.
Во всех измерениях больше четырех есть только три выпуклых правильных многогранника: симплекс как {3,3, ..., 3}, гиперкуб как {4,3, ..., 3}, а кросс-многогранник как {3,3, ..., 4}.[13] В трех измерениях они совпадают с тетраэдром как {3,3}, кубом как {4,3} и октаэдром как {3,4}.
Смотрите также
Рекомендации
- ^ Гарднер (1987): Мартин Гарднер написал популярный отчет о пяти твердых телах в своем декабре 1958 г. Колонка "Математические игры" в журнале Scientific American.
- ^ Зейл, Дональд. "Тимей Платона". Стэнфордская энциклопедия философии.
- ^ Ллойд 2012.
- ^ Вильдберг (1988): Вильдберг обсуждает соответствие Платоновых тел с элементами в Тимей но отмечает, что эта переписка, похоже, была забыта в Эпиномис, который он называет «длинным шагом к теории Аристотеля», и указывает, что эфир Аристотеля стоит выше других четырех элементов, а не находится на равных с ними, что делает соответствие менее уместным.
- ^ Вейл 1952, п. 74.
- ^ Кокстер, Правильные многогранники, сек. 1.8 Конфигурации
- ^ а б c Месхишвили, Мамука (2020). «Средние циклические правильные многоугольники и платоновы тела». Коммуникации в математике и приложениях. 11: 335–355.
- ^ а б Джеррард, Ричард П .; Ветцель, Джон Э .; Юань, Липин (апрель 2017 г.). «Платонические переходы». Математический журнал. Вашингтон, округ Колумбия: Математическая ассоциация Америки. 90 (2): 87–98. Дои:10.4169 / math.mag.90.2.87.
- ^ Шрек, Д. Дж. Э. (1950), "Проблема принца Руперта и ее расширение Питером Ньюландом", Scripta Mathematica, 16: 73–80 и 261–267
- ^ Скриба, Кристоф Дж. (1968), "Проблема принца Рупрехта фон дер Пфальца", Praxis der Mathematik (на немецком), 10 (9): 241–246, МИСТЕР 0497615
- ^ Кляйнерт и Маки (1981)
- ^ Жидкокристаллические голубые фазы (1989). Тамар Сейдеман, Доклады о достижениях физики, Том 53, номер 6
- ^ Кокстер 1973, п. 136.
Источники
- Атья, Майкл; Сатклифф, Пол (2003). «Многогранники в физике, химии и геометрии». Милан Дж. Математика. 71: 33–58. arXiv:math-ph / 0303071. Дои:10.1007 / s00032-003-0014-1.CS1 maint: ref = harv (связь)
- Бойер, Карл; Мерцбах, Ута (1989). История математики (2-е изд.). Вайли. ISBN 0-471-54397-7.
- Кокстер, Х. С. М. (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications. ISBN 0-486-61480-8.CS1 maint: ref = harv (связь)
- Евклид (1956). Хит, Томас Л. (ред.). Тринадцать книг Евклида, книги 10–13 (2-е неабр. Ред.). Нью-Йорк: Dover Publications. ISBN 0-486-60090-4.
- Гарднер, Мартин (1987). 2-я книга журнала Scientific American по математическим головоломкам и решениям, University of Chicago Press, Глава 1: Пять Платоновых тел, ISBN 0226282538
- Геккель, Эрнст, Э. (1904). Kunstformen der Natur. Доступно как Haeckel, E. (1998); Виды искусства в природе, Престел США. ISBN 3-7913-1990-6.
- Кеплер. Йоханнес Strena seu de nive sexangula (На шестигранной снежинке), 1611, статья Кеплера, в которой обсуждалась причина шестиугольной формы снежных кристаллов, а также формы и симметрии в природе. Говорит о платоновых телах.
- Кляйнерт, Хаген И Маки, К. (1981). «Решетчатые текстуры в холестерических жидких кристаллах» (PDF). Fortschritte der Physik. 29 (5): 219–259. Bibcode:1981ForPh..29..219K. Дои:10.1002 / prop.19810290503.CS1 maint: ref = harv (связь)
- Ллойд, Дэвид Роберт (2012). «Сколько лет Платоновым телам?». Бюллетень BSHM: Журнал Британского общества истории математики. 27 (3): 131–140. Дои:10.1080/17498430.2012.670845.CS1 maint: ref = harv (связь)
- Пью, Энтони (1976). Многогранники: визуальный подход. Калифорния: Калифорнийский университет Press в Беркли. ISBN 0-520-03056-7.
- Вейль, Германн (1952). Симметрия. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02374-3.CS1 maint: ref = harv (связь)
- Вильдберг, Кристиан (1988). Иоанн Филопон критиковал теорию эфира Аристотеля. Вальтер де Грюйтер. С. 11–12. ISBN 9783110104462
внешняя ссылка
Эта статья использование внешняя ссылка может не следовать политикам или рекомендациям Википедии. (Декабрь 2019 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Викискладе есть медиафайлы по теме Платоновы тела. |
- Платоновы тела в энциклопедии математики
- Вайсштейн, Эрик В. «Платоново твердое тело». MathWorld.
- Вайсштейн, Эрик В. "Изогедр". MathWorld.
- Книга XIII Евклида Элементы.
- Интерактивные 3D-многогранники в Java
- Платоновы тела в визуальных многогранниках
- Средство просмотра твердых тел представляет собой интерактивную программу просмотра трехмерных многогранников, которая позволяет сохранять модель в формате svg, stl или obj.
- Интерактивное складывание / разворачивание платоновых тел в Java
- Бумажные модели Платоновых тел созданы с использованием сетей, созданных Стелла программного обеспечения
- Платоновы тела Бесплатные бумажные модели (сетки)
- Грайм, Джеймс; Стеклс, Кэти. "Платоновы тела". Numberphile. Брэди Харан.
- Обучение математике с искусством модели, созданные студентами
- Обучение математике с искусством инструкция для учителя по изготовлению моделей
- Каркасы платоновых тел изображения алгебраические поверхности
- Платоновы тела с некоторыми вывод формул
- Как сделать четыре платоновых тела из куба
































































![{displaystyle varphi = 2cos {pi over 5} = {frac {1+ {sqrt {5}}} {2}} qquad xi = 2sin {pi over 5} = {sqrt {frac {5- {sqrt {5}}] } {2}}} = 5 ^ {frac {1} {4}} varphi ^ {- {frac {1} {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7548bc5ac9c880becb586db7748219b025ea2f80)




![{displaystyle S _ {[n]} ^ {(2m)} = {frac {1} {n}} sum _ {i = 1} ^ {n} d_ {i} ^ {2m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96afa0c1c6a4c8a062079f55e03d16851d9a16e2)
![{displaystyle S _ {[4]} ^ {(2)} = S _ {[6]} ^ {(2)} = S _ {[8]} ^ {(2)} = S _ {[12]} ^ {( 2)} = S _ {[20]} ^ {(2)} = R ^ {2} + L ^ {2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86f9e1319c2a21d79886db8b70dd0098a8faa7b1)
![{displaystyle S _ {[4]} ^ {(4)} = S _ {[6]} ^ {(4)} = S _ {[8]} ^ {(4)} = S _ {[12]} ^ {( 4)} = S _ {[20]} ^ {(4)} = (R ^ {2} + L ^ {2}) ^ {2} + {frac {4} {3}} R ^ {2} L ^ {2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a2661f98704e1c41a319db34c601e0f05550ad8)
![{displaystyle S _ {[6]} ^ {(6)} = S _ {[8]} ^ {(6)} = S _ {[12]} ^ {(6)} = S _ {[20]} ^ {( 6)} = (R ^ {2} + L ^ {2}) ^ {3} + 4R ^ {2} L ^ {2} (R ^ {2} + L ^ {2}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f81a712d06c02222b5f0b5432b3c0a688cd176f)
![{displaystyle S _ {[12]} ^ {(8)} = S _ {[20]} ^ {(8)} = (R ^ {2} + L ^ {2}) ^ {4} + 8R ^ {2 } L ^ {2} (R ^ {2} + L ^ {2}) ^ {2} + {frac {16} {5}} R ^ {4} L ^ {4},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23641bea07dc0d15e5a2900c6b968fb621fc9ca5)
![{displaystyle S _ {[12]} ^ {(10)} = S _ {[20]} ^ {(10)} = (R ^ {2} + L ^ {2}) ^ {5} + {frac {40 } {3}} R ^ {2} L ^ {2} (R ^ {2} + L ^ {2}) ^ {3} + 16R ^ {4} L ^ {4} (R ^ {2} + L ^ {2}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a567b9bc39d5d683613748216aa9dc0489797c7)
![{displaystyle S _ {[n]} ^ {(4)} + {frac {16} {9}} R ^ {4} = (S _ {[n]} ^ {(2)} + {frac {2} { 3}} R ^ {2}) ^ {2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5550577716167ecab7d68e60fe0ab8503121eac0)









