WikiDer > Усеченный икосододекаэдр
| Усеченный икосододекаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 62, E = 180, V = 120 (χ = 2) |
| Лица по сторонам | 30{4}+20{6}+12{10} |
| Обозначение Конвея | bD или taD |
| Символы Шлефли | tr {5,3} или |
| т0,1,2{5,3} | |
| Символ Wythoff | 2 3 5 | |
| Диаграмма Кокстера | |
| Группа симметрии | ячас, H3, [5,3], (* 532), заказ 120 |
| Группа вращения | я, [5,3]+, (532), заказ 60 |
| Двугранный угол | 6-10: 142.62° 4-10: 148.28° 4-6: 159.095° |
| Рекомендации | U28, C31, W16 |
| Характеристики | Полурегулярный выпуклый зоноэдр |
 Цветные лица |  4.6.10 (Фигура вершины) |
 Триаконтаэдр Дисдякиса (двойственный многогранник) |  Сеть |
В геометрия, то усеченный икосододекаэдр является Архимедово твердое тело, один из тринадцати выпуклых изогональный непризматические твердые тела, состоящие из двух или более типов правильный многоугольник лица.
Имеет 62 лица: 30 квадраты, 20 обычных шестиугольникии 12 обычных декагоны. У него больше всего ребер и вершин среди всех Платоновых и Архимедовых тел, хотя курносый додекаэдр имеет больше лиц. Из всех вершинно-транзитивных многогранников он занимает наибольший процент (89,80%) объема сферы, в которую он вписан, очень узко превосходя курносый додекаэдр (89,63%) и малый Ромбикосододекаэдр (89,23%), и в меньшей степени опережая Усеченный икосаэдр (86,74%); он также имеет наибольший объем (206,8 кубических единиц), когда длина его ребра равна 1. Из всех вершинно-транзитивных многогранников, не являющихся призмами или антипризмами, он имеет наибольшую сумму углов (90 + 120 + 144 = 354 градуса). в каждой вершине; только призма или антипризма с более чем 60 сторонами будет иметь большую сумму. Поскольку каждая его грань имеет точечную симметрию (эквивалентно 180 ° вращающийся симметрии) усеченный икосододекаэдр представляет собой зоноэдр.
Имена
Название усеченный икосододекаэдр, первоначально предоставленный Иоганн Кеплер, вводит в заблуждение. Фактический усечение из икосододекаэдр имеет прямоугольники вместо квадраты. Этот неоднородный многогранник топологически эквивалент архимедова твердого тела. Альтернативные взаимозаменяемые имена:
|
Название большой ромбоикосододекаэдр относится к отношениям с (маленьким) ромбикосододекаэдр (сравните раздел Рассечение).
Существует невыпуклый однородный многогранник с похожим названием невыпуклый большой ромбоикосододекаэдр.
Площадь и объем
Площадь поверхности А и объем V усеченного икосододекаэдра реберной длины а находятся:[нужна цитата]
Если набор всего 13 Архимедовы тела были построены с одинаковой длиной ребер, усеченный икосододекаэдр будет самым большим.
Декартовы координаты
Декартовы координаты для вершин усеченного икосододекаэдра с длиной ребра 2φ - 2 с центром в начале координат - это все даже перестановки из:[4]
- (±1/φ, ±1/φ, ±(3 + φ)),
- (±2/φ, ±φ, ±(1 + 2φ)),
- (±1/φ, ±φ2, ±(−1 + 3φ)),
- (±(2φ − 1), ±2, ±(2 + φ)) и
- (±φ, ±3, ±2φ),
куда φ = 1 + √5/2 это Золотое сечение.
Рассечение
Усеченный икосододекаэдр - это выпуклый корпус из ромбикосододекаэдр с кубоиды над его 30 квадратами, отношение высоты к основанию которых φ. Остальное его пространство можно разделить на неоднородные купола, а именно 12 между внутренними пятиугольниками и внешними декагонами и 20 между внутренними треугольниками и внешними шестиугольниками.
Альтернативное рассечение также имеет ромбикосододекаэдрическое ядро. Имеет 12 пятиугольные ротонды между внутренними пятиугольниками и внешними декагонами. Оставшаяся часть - это тороидальный многогранник.
| рассечение изображений |
|---|
Эти изображения показывают ромбикосододекаэдр (фиолетовый) и усеченный икосододекаэдр (зеленый). Если длина их ребер равна 1, расстояние между соответствующими квадратами равно φ. |
Ортогональные проекции
Усеченный икосододекаэдр имеет семь особых ортогональные проекции, с центром на вершине, на трех типах ребер и трех типах граней: квадратной, шестиугольной и десятиугольной. Последние два соответствуют букве A2 и H2 Самолеты Кокстера.
| В центре | Вершина | Край 4-6 | Край 4-10 | Край 6-10 | Лицо квадрат | Лицо шестиугольник | Лицо десятиугольник |
|---|---|---|---|---|---|---|---|
| Твердый |  |  |  | ||||
| Каркас | 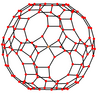 |  | 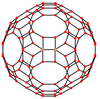 |  |  |  |  |
| Проективный симметрия | [2]+ | [2] | [2] | [2] | [2] | [6] | [10] |
| Двойной изображение |  |  |  |  | 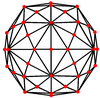 |  | 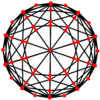 |
Сферические мозаики и диаграммы Шлегеля
Усеченный икосододекаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
Диаграммы Шлегеля похожи, с перспективная проекция и прямые края.
| Ортографическая проекция | Стереографические проекции | ||
|---|---|---|---|
| Декагон-центрированный | Шестиугольник-центрированный | Квадрат-центрированный | |
 |  |  | 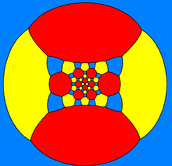 |
Геометрические вариации
В Икосаэдрическая симметрия есть неограниченные геометрические вариации усеченный икосододекаэдр с изогональный лица. В усеченный додекаэдр, ромбикосододекаэдр, и усеченный икосаэдр как вырожденные предельные случаи.
 |  |  |  |  |  |  |  |
Усеченный икосододекаэдрический граф
| Усеченный икосододекаэдрический граф | |
|---|---|
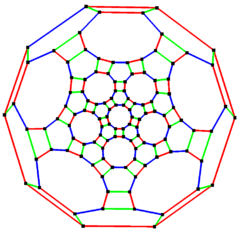 5-кратная симметрия | |
| Вершины | 120 |
| Края | 180 |
| Радиус | 15 |
| Диаметр | 15 |
| Обхват | 4 |
| Автоморфизмы | 120 (А5×2) |
| Хроматическое число | 2 |
| Характеристики | Кубический, Гамильтониан, обычный, нулевой симметричный |
| Таблица графиков и параметров | |
в математический поле теория графов, а усеченный икосододекаэдрический граф (или же большой ромбоикосододекаэдрический граф) это граф вершин и ребер усеченного икосододекаэдра, один из Архимедовы тела. Имеет 120 вершины и 180 ребер, и является нулевой симметричный и кубический Архимедов граф.[5]
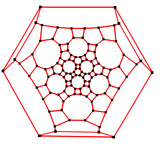 3-х кратная симметрия | 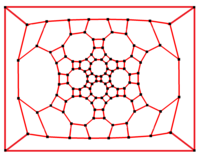 2-х кратная симметрия |
Связанные многогранники и мозаики
 |  |
| Икосаэдр-бабочка и додекаэдр содержат две трапециевидные грани вместо квадрата.[6] | |
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Этот многогранник можно рассматривать как член последовательности однородных узоров с вершиной фигуры (4.6.2п) и Диаграмма Кокстера-Дынкина ![]()
![]()
![]()
![]()
![]() . За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.
. За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.
| *п32 мутации симметрии полностью усеченных мозаик: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п32 [п,3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |  |  |  |  |  |  |  |  |  |  |  |
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Примечания
- ^ Веннингер (модель 16, стр.30)
- ^ Уильямсон (Раздел 3-9, с. 94)
- ^ Кромвель (стр.82)
- ^ Вайсштейн, Эрик В. «Икосаэдрическая группа». MathWorld.
- ^ Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269
- ^ Симметроэдры: многогранники из симметричного размещения правильных многоугольников Крейг С. Каплан
Рекомендации
- Веннингер, Магнус (1974), Модели многогранников, Издательство Кембриджского университета, ISBN 978-0-521-09859-5, МИСТЕР 0467493
- Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN 0-521-55432-2.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X.
- Cromwell, P .; Многогранники, CUP hbk (1997), pbk. (1999).
- Эрик В. Вайсштейн, Большой ромбоикосододекаэдр (Архимедово твердое тело) в MathWorld.
- Клитцинг, Ричард. «3D выпуклые равномерные многогранники x3x5x - сетка».
внешняя ссылка
- Вайсштейн, Эрик В. «Большой ромбоикосододекаэдр». MathWorld.
- * Вайсштейн, Эрик В. «Большой ромбоикосододекаэдрический граф». MathWorld.
- Редактируемая сетка усеченного икосододекаэдра для печати с интерактивным трехмерным изображением
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников
















































