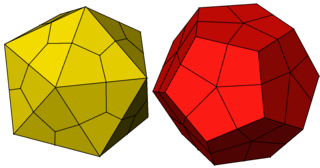
WikiDer > Дельтоидальный гексеконтаэдр
| Дельтоидальный гексеконтаэдр | |
|---|---|
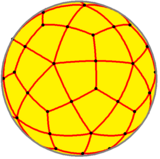
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Каталонский |
| Обозначение Конвея | oD или deD |
| Диаграмма Кокстера | |
| Многоугольник лица |  летающий змей |
| Лица | 60 |
| Края | 120 |
| Вершины | 62 = 12 + 20 + 30 |
| Конфигурация лица | V3.4.5.4 |
| Группа симметрии | ячас, H3, [5,3], (*532) |
| Группа вращения | Я, [5,3]+, (532) |
| Двугранный угол | 154 ° 7 ′ 17 ′ ′ arccos (-19-8√5/41) |
| Характеристики | выпуклый, лицо переходный |
 ромбоикосододекаэдр (двойственный многогранник) |  Сеть |
В геометрия, а дельтовидный гексеконтаэдр (также иногда называют трапециевидный шестиугольник, а стромбический гексеконтаэдр, или тетрагональный гексаконтаэдр[1]) это Каталонский твердый какой двойственный многогранник из ромбоикосододекаэдр, Архимедово твердое тело. Это одно из шести каталонских твердых тел, у которых нет Гамильтонов путь среди его вершин.[2]
Он топологически идентичен невыпуклому ромбический гексеконтаэдр.
Длина и углы
60 лиц - дельтовидные или воздушные змеи. Короткие и длинные края каждого змея находятся в соотношении 1:7 + √5/6 ≈ 1:1.539344663...
Угол между двумя короткими гранями одной грани равен arccos (-5-2√5/20) ≈118.2686774705 °. Противоположный угол между длинными кромками равен arccos (-5+9√5/40) ≈67.783011547435 °. Два других угла каждой грани, между короткой и длинной кромкой каждый, равны arccos (5-2√5/10)≈86.97415549104°.
Двугранный угол между любой парой смежных граней равен arccos (-19-8√5/41)≈154.12136312578°.
Топология
Топологически дельтовидный гексеконтаэдр идентичен невыпуклому ромбический гексеконтаэдр. Дельтоидальный гексеконтаэдр может быть получен из додекаэдр (или же икосаэдр), сдвинув центры граней, центры краев и вершины на разные радиусы от центра тела. Радиусы выбираются так, чтобы полученная форма имела плоские грани змейки, каждая так, чтобы вершины переходили в углы степени 3, грани - в углы степени пять, а центры краев - в точки степени четыре.
Ортогональные проекции
В дельтовидный гексеконтаэдр имеет 3 позиции симметрии, расположенные на 3-х типах вершин:
| Проективный симметрия | [2] | [2] | [2] | [2] | [6] | [10] |
|---|---|---|---|---|---|---|
| Изображение |  |  |  |  |  |  |
| Двойной изображение |  |  |  |  |  |  |
Вариации

В дельтовидный гексеконтаэдр может быть построена либо из правильный икосаэдр или же правильный додекаэдр добавляя вершины к середине и середине грани, и создавая новые ребра от центра каждого ребра к центрам грани. Обозначения многогранника Конвея дал бы их как oI и oD, орто-икосаэдр и ортододекаэдр. Эти геометрические вариации существуют как континуум с одной степенью свободы.
Связанные многогранники и мозаики
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
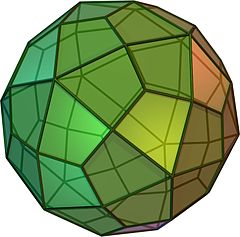
При проецировании на сферу (см. Справа) видно, что края составляют ребра икосаэдра и додекаэдра расположены в своих двойных положениях.
Эта мозаика топологически связана как часть последовательности дельтоидальных многогранников с гранью (V3.4.п.4) и продолжается как мозаика гиперболическая плоскость. Эти лицо переходный цифры имеют (*п32) Reflectional (отражающий) симметрия.
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Фигура Конфиг. |  V3.4.2.4 |  V3.4.3.4 |  V3.4.4.4 |  V3.4.5.4 |  V3.4.6.4 |  V3.4.7.4 |  V3.4.8.4 |  V3.4.∞.4 |
Смотрите также
Рекомендации
- ^ Конвей, Симметрии вещей, стр.284-286.
- ^ http://mathworld.wolfram.com/ArchimedeanDualGraph.html
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5 [1] (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, стр. 286, тетрагональный гексеконтаэдр)
- http://mathworld.wolfram.com/ArchimedeanDualGraph.html
внешняя ссылка
- Эрик В. Вайсштейн, Дельтоидальный гексаконтаэдр и гамильтонов путь (Каталонский твердый) в MathWorld.
- Дельтоидальный гексеконтаэдр (Trapezoidal Hexecontrahedron)—Модель интерактивного многогранника
- Пример из жизни- Мяч диаметром почти 4 метра, из нейлона рипстоп, надутый ветром. Он подпрыгивает по земле, так что дети могут играть с ним на фестивалях воздушных змеев.
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |