WikiDer > Пятиугольный икоситетраэдр

Pentagonal icositetrahedron

Пятиугольный икоситетраэдр
(Щелкните против часовой стрелки* или же cw для вращающихся моделей.)*
Тип	Каталонский
Обозначение Конвея	gC
Диаграмма Кокстера
Многоугольник лица	неправильный пятиугольник
Лица	24
Края	60
Вершины	38 = 6 + 8 + 24
Конфигурация лица	V3.3.3.3.4
Двугранный угол	136° 18' 33'
Группа симметрии	О, ½BC₃, [4,3]⁺, 432
Двойной многогранник	курносый куб
Характеристики	выпуклый, лицо переходный, хиральный
Сеть

3d модель пятиугольного икоситетраэдра

В геометрия, а пятиугольный икоситетраэдр или же пятиугольный икосикатетраэдр^[1] это Каталонский твердый какой двойной из курносый куб. В кристаллография его также называют гироид.^[2]^[3]

Он имеет две различные формы: зеркальные изображения (или же "энантиоморфы") друг друга.

Строительство

Пятиугольный икоситетраэдр можно построить из курносого куба, не взяв двойника. Квадратные пирамиды добавляются к шести квадратным граням курносого куба, а треугольные пирамиды добавляются к восьми треугольным граням, не имеющим общего ребра с квадратом. Высота пирамиды настроена так, чтобы сделать их копланарными с другими 24 треугольными гранями курносого куба. В результате получился пятиугольный икоситетраэдр.

Декартовы координаты

Обозначим постоянная трибоначчи к ${ Displaystyle т приблизительно 1,839 , 286 , 755 , 21}$ . (Видеть курносый куб для геометрического объяснения постоянной трибоначчи.) Тогда Декартовы координаты для 38 вершин пятиугольного икоситетраэдра с центром в начале координат следующие:

12 даже перестановки из (± 1, ± (2t + 1), ± t²) с четным числом знаков минус
12 нечетные перестановки из (± 1, ± (2t + 1), ± t²) с нечетным количеством знаков минус
6 баллов (± t³, 0, 0), (0, ± t³, 0) и (0, 0, ± t³)
8 баллов (± t², ± t², ± t²)

Геометрия

Пятиугольные грани имеют четыре угла ${ Displaystyle arccos ((1-т) / 2) приблизительно 114,812 , 074 , 477 , 90 ^ { circ}}$ и один угол ${ displaystyle arccos (2-t) приблизительно 80.751 , 702 , 088 , 39 ^ { circ}}$ . Пентагон имеет три коротких края единичной длины и два длинных края длины. ${ Displaystyle (т + 1) / 2 приблизительно 1,419 , 643 , 377 , 607 , 08}$ . Острый угол находится между двумя длинными краями. Двугранный угол равен ${ displaystyle arccos (-1 / (t ^ {2} -2)) приблизительно 136.309 , 232 , 892 , 32 ^ { circ}}$ .

Если его двойная курносый куб имеет единичную длину кромки, площадь поверхности и объем:^[4]

{ displaystyle { begin {align} A & = 3 { sqrt { frac {22 (5t-1)} {4t-3}}} && приблизительно 19,299 , 94 V & = { sqrt { frac {11 (t-4)} {2 (20t-37)}}} && приблизительно 7,4474 end {align}}}

Ортогональные проекции

В пятиугольный икоситетраэдр имеет три положения симметрии: два по центру вершин и одно по краю.

Ортогональные проекции
Проективный симметрия	[3]	[4]⁺	[2]
Изображение
Двойной изображение

Вариации

Изоэдральный варианты с той же хиральной октаэдрической симметрией могут быть построены с пятиугольными гранями, имеющими 3 длины ребра.

Показанный вариант можно построить, добавив пирамиды к 6 квадратным граням и 8 треугольным граням курносый куб таким образом, что новые треугольные грани с 3 копланарными треугольниками сливаются в идентичные грани пятиугольника.

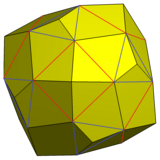Курносый куб с увеличенными пирамидами и объединенными гранями	Пятиугольный икоситетраэдр	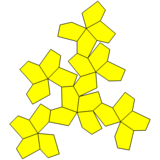Сеть

Связанные многогранники и мозаики

Сферический пятиугольный икоситетраэдр

Этот многогранник топологически связан как часть последовательности многогранников и мозаик пятиугольников с конфигурации лица (V3.3.3.3.п). (Последовательность переходит в разбиение гиперболической плоскости на любую п.) Эти лицо переходный фигуры имеют (n32) вращательные симметрия.

п32 мутации симметрии курносых плиток: 3.3.3.3.n v т е
Симметрия п32	Сферический				Евклидово	Компактный гиперболический		Paracomp.
Симметрия п32	232	332	432	532	632	732	832	∞32
Курносый цифры
Конфиг.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Гироскоп цифры
Конфиг.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

В пятиугольный икоситетраэдр является вторым в серии двойственных курносых многогранников и мозаик с конфигурация лица V3.3.4.3.п.

4п2 мутации симметрии курносых плиток: 3.3.4.3.n [ v т е ]
Симметрия 4п2	Сферический		Евклидово	Компактный гиперболический				Paracomp.
Симметрия 4п2	242	342	442	542	642	742	842	∞42
Курносый цифры
Конфиг.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Гироскоп цифры
Конфиг.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Пентагональный икоситетраэдр является одним из семейства двойственных однородных многогранников, связанных с кубом и правильным октаэдром.

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s₂{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час₂{4,3} т {3,3}	с {3,4} с {3^1,1}

		=	=	=				= или же	= или же	=

Двойники к однородным многогранникам
V4³	V3.8²	V (3,4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵