WikiDer > Ромбокубооктаэдр
| Ромбокубооктаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 26, E = 48, V = 24 (χ = 2) |
| Лица по сторонам | 8{3}+(6+12){4} |
| Обозначение Конвея | eC или aaC аааТ |
| Символы Шлефли | rr {4,3} или |
| т0,2{4,3} | |
| Символ Wythoff | 3 4 | 2 |
| Диаграмма Кокстера | |
| Группа симметрии | Очас, B3, [4,3], (* 432), порядок 48 |
| Группа вращения | О, [4,3]+, (432), заказ 24 |
| Двугранный угол | 3-4: 144°44′08″ (144.74°) 4-4: 135° |
| Рекомендации | U10, C22, W13 |
| Характеристики | Полурегулярный выпуклый |
 Цветные лица |  3.4.4.4 (Фигура вершины) |
 Дельтоидный икоситетраэдр (двойственный многогранник) |  Сеть |
В геометрия, то ромбокубооктаэдр, или же малый ромбокубооктаэдр, является Архимедово твердое тело с восемью треугольный и восемнадцать квадрат лица. Есть 24 идентичных вершины, в каждой из которых сходятся один треугольник и три квадрата. (Обратите внимание, что шесть квадратов имеют общие вершины только с треугольниками, а остальные двенадцать имеют одно ребро.) многогранник имеет октаэдрическая симметрия, словно куб и октаэдр. Его двойной называется дельтовидный икоситетраэдр или трапециевидный икоситетраэдр, хотя его грани на самом деле не соответствуют действительности трапеции.
Имена
Иоганн Кеплер в Harmonices Mundi (1618) назвал этот многогранник a ромбокубооктаэдр, сокращение от усеченный кубооктаэдрический ромб, с кубооктаэдрический ромб быть его именем для ромбический додекаэдр.[1] Есть разные усечения ромбического додекаэдра в топологический ромбокубооктаэдр: в основном его исправление (слева), тот, который создает однородное твердое тело (в центре), и выпрямление двойного кубооктаэдр (справа), который является ядром двойное соединение.
Его также можно назвать расширенный или же скошенный куб или же октаэдр, из операций усечения на любом равномерный многогранник.
Геометрические отношения

Имеются искажения ромбокубооктаэдра, которые, хотя некоторые из граней не являются правильными многоугольниками, по-прежнему однородны по вершинам. Некоторые из них можно сделать, если взять куб или октаэдр и отрезать края, а затем обрезать углы, так что полученный многогранник имеет шесть квадратных и двенадцать прямоугольных граней. Они обладают октаэдрической симметрией и образуют непрерывный ряд между кубом и октаэдром, аналогично искажениям куба. ромбикосододекаэдр или тетраэдрические искажения кубооктаэдр. Однако ромбокубооктаэдр также имеет второй набор искажений с шестью прямоугольными и шестнадцатью трапециевидными гранями, которые не обладают октаэдрической симметрией, а скорее Tчас симметрии, поэтому они инвариантны относительно тех же вращений, что и тетраэдр но разные размышления.
Линии, по которым Кубик Рубика можно повернуть, спроецировать на сферу, подобное, топологически идентичны ребрам ромбокубооктаэдра. Фактически были созданы варианты, использующие механизм кубика Рубика, которые очень напоминают ромбокубооктаэдр.[2][3]
Ромбокубооктаэдр используется в трех однородные мозаики, заполняющие пространство: the канеллированные кубические соты, то усеченные кубические соты, а чередующиеся кубические соты.
Рассечение
Ромбокубооктаэдр можно разрезать на два квадратные купола и центральный восьмиугольная призма. Поворот одного купола на 45 градусов создает псевдоромбокубооктаэдр. Оба этих многогранника имеют одинаковую фигуру вершины: 3.4.4.4.
Есть три пары параллельных плоскостей, каждая из которых пересекает ромбокубооктаэдр в правильном восьмиугольнике. Ромбокубооктаэдр можно разделить вдоль любого из них, чтобы получить восьмиугольную призму с правильными гранями и двумя дополнительными многогранниками, называемыми квадратными. купола, которые входят в число Твердые тела Джонсона; Таким образом, это удлиненный квадрат ортодвуполая. Эти части можно собрать заново, чтобы получить новое твердое тело, называемое удлиненная квадратная гиробикупола или же псевдоромбокубооктаэдр, с симметрией квадратной антипризмы. В этом случае все вершины локально такие же, как у ромбокубооктаэдра, с одним треугольником и тремя квадратами, сходящимися в каждом, но не все они идентичны по отношению ко всему многограннику, поскольку некоторые из них ближе к оси симметрии, чем другие.
 |  Ромбокубооктаэдр |
 Псевдоромбокубооктаэдр |
Ортогональные проекции
В ромбокубооктаэдр имеет шесть специальных ортогональные проекциипо центру на вершине, на двух типах ребер и трех типах граней: треугольниках и двух квадратах. Последние два соответствуют букве B2 и А2 Самолеты Кокстера.
| В центре | Вершина | Край 3-4 | Край 4-4 | Лицо Квадрат-1 | Лицо Квадрат-2 | Лицо Треугольник |
|---|---|---|---|---|---|---|
| Твердый |  |  |  | |||
| Каркас | 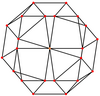 |  |  | 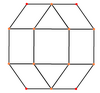 |  |  |
| Проективный симметрия | [2] | [2] | [2] | [2] | [4] | [6] |
| Двойной | 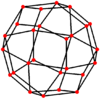 |  | 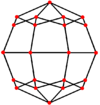 |  | 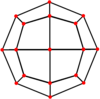 |  |
Сферическая черепица
Ромбокубооктаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.
 |  (6) квадрат-центрированный |  (6) квадрат-центрированный |  (8) треугольник-центрированный |
| Ортогональная проекция | Стереографические проекции | ||
|---|---|---|---|
Пиритоэдрическая симметрия
Полусимметричная форма ромбокубооктаэдра, ![]()
![]()
![]()
![]()
![]() , существует с пиритоэдрическая симметрия, [4,3+], (3 * 2) как Диаграмма Кокстера
, существует с пиритоэдрическая симметрия, [4,3+], (3 * 2) как Диаграмма Кокстера ![]()
![]()
![]()
![]()
![]() , Символ Шлефли s2{3,4}, и его можно назвать кантик курносый октаэдр. Эту форму можно визуализировать, поочередно раскрашивая края 6 квадраты. Эти квадраты можно затем превратить в прямоугольники, а 8 треугольников остаются равносторонними. 12 диагональных квадратных граней станут равнобедренные трапеции. В пределе прямоугольники можно свести к краям, а трапеции - в треугольники, а икосаэдр формируется курносый октаэдр строительство,
, Символ Шлефли s2{3,4}, и его можно назвать кантик курносый октаэдр. Эту форму можно визуализировать, поочередно раскрашивая края 6 квадраты. Эти квадраты можно затем превратить в прямоугольники, а 8 треугольников остаются равносторонними. 12 диагональных квадратных граней станут равнобедренные трапеции. В пределе прямоугольники можно свести к краям, а трапеции - в треугольники, а икосаэдр формируется курносый октаэдр строительство, ![]()
![]()
![]()
![]()
![]() , с {3,4}. (The соединение двух икосаэдров строится из обоих чередующихся позиций.)
, с {3,4}. (The соединение двух икосаэдров строится из обоих чередующихся позиций.)
| Вариации пиритоэдрической симметрии | |||||||||
|---|---|---|---|---|---|---|---|---|---|
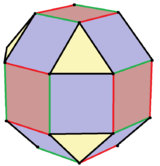 Единая геометрия |  Неоднородная геометрия |  Неоднородная геометрия | 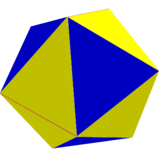 В пределе икосаэдр курносый октаэдр, с одной из двух позиций. |  Соединение двух икосаэдров из обоих чередующихся позиций. | |||||
Алгебраические свойства
Декартовы координаты
Декартовы координаты для вершин ромбокубооктаэдра с центром в начале координат, с длиной ребра 2 единицы, являются все даже перестановки из
- (±1, ±1, ±(1 + √2)).
Если исходный ромбокубооктаэдр имеет единичную длину ребра, его двойственный стромбический икозитетраэдр имеет длину кромки
Площадь и объем
Площадь А и объем V ромбокубооктаэдра длины ребра а находятся:
Плотность плотной упаковки
Оптимальный фракция упаковки ромбокубооктаэдров определяется выражением
- .
Было замечено, что это оптимальное значение получается в Решетка Браве по де Грааф (2011). Поскольку ромбокубооктаэдр содержится в ромбический додекаэдр чей вписанная сфера идентична его собственной вписанной сфере, значение оптимальной фракции упаковки является следствием Гипотеза Кеплера: этого можно добиться, поместив ромбокубооктаэдр в каждую ячейку ромбические додекаэдрические соты, и его невозможно превзойти, так как в противном случае оптимальную плотность упаковки сфер можно было бы превзойти, поместив сферу в каждый ромбокубооктаэдр гипотетической упаковки, которая ее превосходит.
В искусстве
1495 год Портрет Луки Пачоли, традиционно относят к Якопо де Барбари, включает стеклянный ромбокубооктаэдр, наполовину заполненный водой, который, возможно, был окрашен Леонардо да Винчи.[5]Первая печатная версия ромбокубооктаэдра была написана Леонардо и появилась в Пачолис Divina пропорционально (1509).
Сферическую панораму 180 ° × 360 ° можно спроецировать на любой многогранник; но ромбокубооктаэдр дает достаточно хорошее приближение к сфере, хотя его легко построить. Этот вид проекции называется Филосфера, возможно из некоторых программ для сборки панорам. Он состоит из двух изображений, которые печатаются отдельно и вырезаются ножницами, оставляя некоторые клапаны для сборки с помощью клея.[6]
Объекты
В Freescape игры Бурильщик и Темная сторона у обоих была игровая карта в виде ромбокубооктаэдра.
Галактика "Торопись-Снег" и "Галактика морского оползня" в видеоигре Супер Марио Галактика имеют планеты в форме ромбокубооктаэдра.
Ежик Соник 3's Зона Ледяной шапки представляет собой столбы, увенчанные ромбокубооктаэдрами.
Вовремя Кубик Рубика В моде 1980-х годов по крайней мере две проданные извилистые головоломки имели форму ромбокубооктаэдра (механизм был похож на механизм Кубик Рубика).[2][3]
Связанные многогранники
Ромбокубооктаэдр - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | т {4,3} | г {4,3} г {31,1} | т {3,4} т {31,1} | {3,4} {31,1} | рр {4,3} s2{3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | час2{4,3} т {3,3} | с {3,4} с {31,1} |
= | = | = | ||||||||
| Двойники к однородным многогранникам | ||||||||||
| V43 | V3.82 | V (3,4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
Мутации симметрии
Этот многогранник топологически связан как часть последовательности скошенный многогранники с вершиной фигуры (3.4.п.4) и продолжается как мозаика гиперболическая плоскость. Эти вершинно-транзитивный цифры имеют (*п32) Reflectional (отражающий) симметрия.
| *п32 мутации симметрии расширенных мозаик: 3.4.п.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paracomp. | ||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Фигура |  |  |  |  |  |  |  | |
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
| *п42 мутации симметрии расширенных мозаик: п.4.4.4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия [n, 4], (*п42) | Сферический | Евклидово | Компактный гиперболический | Paracomp. | |||||||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4] | *∞42 [∞,4] | |||||
| Расширенный цифры |  |  |  |  |  |  |  | ||||
| Конфиг. | 3.4.4.4 | 4.4.4.4 | 5.4.4.4 | 6.4.4.4 | 7.4.4.4 | 8.4.4.4 | ∞.4.4.4 | ||||
| Ромбический цифры config. |  V3.4.4.4 |  V4.4.4.4 |  V5.4.4.4 |  V6.4.4.4 |  V7.4.4.4 |  V8.4.4.4 |  V∞.4.4.4 | ||||
Расположение вершин
У него общее расположение вершин с тремя невыпуклые равномерные многогранники: the звездчатый усеченный шестигранник, то малый ромбогексаэдр (имеющий треугольные грани и шесть квадратных граней вместе), а малый кубокубооктаэдр (имеет двенадцать общих квадратных граней).
 Ромбокубооктаэдр |  Малый кубокубооктаэдр |  Малый ромбогексаэдр |  Звездчатый усеченный шестигранник |
| Ромбокубооктаэдрический граф | |
|---|---|
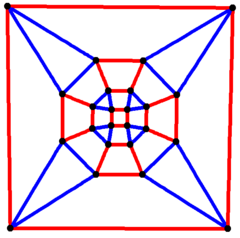 4-х кратная симметрия | |
| Вершины | 24 |
| Края | 48 |
| Автоморфизмы | 48 |
| Характеристики | Граф четвертого порядка, Гамильтониан, обычный |
| Таблица графиков и параметров | |
Ромбокубооктаэдрический граф
в математический поле теория графов, а ромбокубооктаэдрический граф это граф вершин и ребер ромбокубооктаэдра, один из Архимедовы тела. Имеет 24 вершины и 48 ребер, и является график четвертой степени Архимедов граф.[7]
Смотрите также
- Соединение пяти ромбокубооктаэдров
- Куб
- Кубооктаэдр
- Невыпуклый большой ромбокубооктаэдр
- Усеченный ромбокубооктаэдр
- Гиробикупола удлиненная квадратная
- Моравская звезда
- Октаэдр
- Ромбикосододекаэдр
- Змея Рубика - головоломка, которая может образовывать ромбокубооктаэдрический «шар»
- Национальная библиотека Беларуси - его архитектурная основная составляющая имеет форму ромбокубооктаэдра.
- Усеченный кубооктаэдр (большой ромбокубооктаэдр)
Рекомендации
- ^ Гармонии Мира Иоганна Кеплера, Перевод на английский язык с введением и примечаниями Э. Дж. Эйтон, А. М. Дункан, Дж. В. Филд, 1997, ISBN 0-87169-209-0 (стр.119)
- ^ а б "Советский шар-пазл". TwistyPuzzles.com. Получено 23 декабря 2015.
- ^ а б "Головоломка в алмазном стиле". Страница головоломок Яапа. Получено 31 мая 2017.
- ^ RitrattoPacioli.it
- ^ Маккиннон, Ник (1993). "Портрет фра Лука Пачоли". Математический вестник. 77 (479): 143. Дои:10.2307/3619717.
- ^ Филосфера
- ^ Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, стр. 269
дальнейшее чтение
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN 0-521-55432-2.
- Кокстер, H.S.M.; Longuet-Higgins, M.S .; Миллер, J.C.P. (13 мая 1954 г.). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия A, Математические и физические науки. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. Дои:10.1098 / рста.1954.0003.
- de Graaf, J .; van Roij, R .; Дейкстра, М. (2011), "Плотные регулярные упаковки нерегулярных невыпуклых частиц", Phys. Rev. Lett., 107: 155501, arXiv:1107.0603, Bibcode:2011PhRvL.107o5501D, Дои:10.1103 / PhysRevLett.107.155501, PMID 22107298
- Betke, U .; Хенк, М. (2000), "Плотные решетчатые упаковки 3-многогранников", Comput. Геом., 16: 157, arXiv:математика / 9909172, Дои:10.1016 / S0925-7721 (00) 00007-9
- Torquato, S .; Цзяо, Ю. (2009), "Плотные упаковки платоновых и архимедовых тел", Природа, 460: 876, arXiv:0908.4107, Bibcode:2009Натура.460..876Т, Дои:10.1038 / природа08239, PMID 19675649
- Хейлз, Томас К. (2005), "Доказательство гипотезы Кеплера", Анналы математики, 162: 1065, arXiv:математика / 9811078v2, Дои:10.4007 / анналы.2005.162.1065
внешняя ссылка
| Викискладе есть медиафайлы по теме Ромбокубооктаэдр. |
- Эрик В. Вайсштейн, Ромбокубооктаэдр (Архимедово твердое тело) в MathWorld.
- Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3o4x - sirco".
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников
- Редактируемая сетка для печати ромбокубооктаэдра с интерактивным трехмерным изображением
- Ромбокубооктаэдр Звезда Шандор Кабаи, Вольфрам Демонстрационный проект.
- Ромбокубооктаэдр: бумажные полоски для плетения


























































