WikiDer > Cantellation (геометрия)

Cantellation (geometry)

А скошенный куб - Красные лица уменьшены. Края скошены, образуя новые желтые квадратные грани. Вершины усекаются, образуя новые синие треугольные грани.

А скошенный кубические соты - Фиолетовые кубики косоугольные. Края скошены, образуя новые синие кубические ячейки. Вершины усекаются, образуя новые красные ректификованный куб клетки.

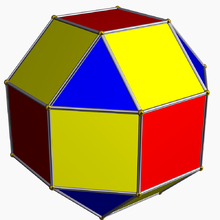
В геометрия, а песня является усечением 2-го порядка в любом измерении, которое скашивает правильный многогранник на его краях и в его вершинах, создавая новый фасет вместо каждого ребра и каждой вершины. Cantellation также относится к правильные мозаики и соты. Cantellating также исправляет исправление.

Кантелляцию (для многогранников и мозаик) также называют расширение к Алисия Буль Стотт: это соответствует перемещению граней правильной формы от центра и заполнению новой гранью в промежутке для каждого открытого ребра и для каждой открытой вершины.

Обозначение

Скошенный многогранник представлен расширенным Schl 盲 fli символ т_0,2{п,q,...} или же р ${displaystyle {egin {Bmatrix} p q ... end {Bmatrix}}}$ или же rr{п,q,...}.

За многогранники, песня предлагает прямую последовательность из правильный многогранник к его двойной.

Пример: последовательность раскосов между кубом и октаэдром:

Пример: а кубооктаэдр это канеллированный тетраэдр.

Для многомерных многогранников кантелевидение предлагает прямую последовательность от правильного многогранника к его двунаправленный форма.

Примеры: складывающиеся многогранники, мозаики.

Правильные многогранники, правильные мозаики
Форма	Многогранники			Плитки
Coxeter	rTT	rCO	избавлять	rQQ	rH 螖
Конвей обозначение	eT	eC = eO	eI = eD	eQ	eH = e 螖
Многогранники к быть расширенным	Тетраэдр	Куб или же октаэдр	Икосаэдр или же додекаэдр	Квадратная плитка	Шестиугольная черепица Треугольная черепица
Многогранники к быть расширенным
Изображение
Анимация

Равномерные многогранники или их двойники
Coxeter	rrt {2,3}	rrs {2,6}	rrCO	rrID
Конвей обозначение	eP3	eA4	eaO = eaC	eaI = eaD
Многогранники к быть расширенным	Треугольная призма или же треугольная бипирамида	Квадратная антипризма или же тетрагональный трапецииэдр	Кубооктаэдр или же ромбический додекаэдр	Икосододекаэдр или же ромбический триаконтаэдр
Многогранники к быть расширенным
Изображение
Анимация