WikiDer > Джонсон солид

Johnson solid

В удлиненная квадратная гиробикупола (J₃₇), твердое тело Джонсона

Этот 24 равностороннего треугольника пример не является твердым телом Джонсона, потому что он не выпуклый.

Этот пример с 24 квадратами не является твердым телом Джонсона, потому что он не является строго выпуклым (имеет 180 ° двугранные углы.)

В геометрия, а Джонсон солид строго выпуклый многогранник каждое лицо которого является правильный многоугольник. Нет требования, чтобы каждая грань должна быть одним и тем же многоугольником, или что одни и те же многоугольники соединяются вокруг каждой вершины. Примером твердого тела Джонсона является квадратный пирамида с равносторонний стороны (J₁); у него 1 квадратная грань и 4 треугольных грани. Некоторые авторы требуют, чтобы твердое тело не униформа (т.е. не Платоново твердое тело, Архимедово твердое тело, однородная призма, или униформа антипризма), прежде чем они назовут его «твердым телом Джонсона».

Как и в любом строго выпуклом твердом теле, по крайней мере три грани пересекаются в каждой вершине, а сумма их углов меньше 360 градусов. Так как правильный многоугольник имеет углы не менее 60 градусов, отсюда следует, что не более пяти граней пересекаются в любой вершине. В пятиугольная пирамида (J₂) - это пример с вершиной пятой степени.

Хотя нет очевидного ограничения, что любой заданный правильный многоугольник не может быть гранью тела Джонсона, оказывается, что грани тел Джонсона, которые не являются униформа (т.е. не Платоново твердое тело, Архимедово твердое тело, однородная призма, или униформа антипризма) всегда имеет 3, 4, 5, 6, 8 или 10 сторон.

В 1966 г. Норман Джонсон опубликовал список, в который вошли все 92 тела Джонсона (исключая 5 Платоновых тел, 13 Архимедовых тел, бесконечно много однородных призм и бесконечное множество однородных антипризм), и дал им их имена и номера. Он не доказал, что их было всего 92, но предположил, что других не было. Виктор Залгаллер в 1969 году доказал, что список Джонсона был полным.

Из твердых тел Джонсона удлиненная квадратная гиробикупола (J₃₇), также называемый псевдоромбокубооктаэдром,^[1] уникальна тем, что локально однородна по вершинам: в каждой вершине по 4 грани, и их расположение всегда одинаково: 3 квадрата и 1 треугольник. Однако он не является вершинно-транзитивным, поскольку имеет разную изометрию в разных вершинах, что делает его твердым телом Джонсона, а не телом. Архимедово твердое тело.

Имена

Именование твердых тел Джонсона следует гибкой и точной описательной формуле, так что многие твердые тела могут быть названы по-разному без ущерба для их точности описания. Большинство твердых тел Джонсона можно построить из первых нескольких (пирамиды, купола, и ротонда) вместе с Платонический и Архимедов твердые вещества призмы, и антипризмы; центр названия конкретного твердого вещества будет отражать эти ингредиенты. Оттуда к слову добавляется серия префиксов, обозначающих добавления, вращения и преобразования:

Би- указывает, что две копии рассматриваемого твердого тела соединены основанием к основанию. Для куполов и ротондов твердые тела можно соединять так, чтобы одинаковые грани (орто-) или непохожие лица (гиро-) встретить. Используя эту номенклатуру, октаэдр можно описать как квадратная бипирамида, а кубооктаэдр как треугольная гиробикупола, и икосододекаэдр как пятиугольная гиробиротонда.
Удлиненный указывает на призма соединяется с основанием рассматриваемого твердого тела или между основаниями в случае твердого вещества Bi. А ромбокубооктаэдр таким образом можно описать как ортобикупола удлиненная квадратная.
Гиро-удлиненный указывает на антипризма соединяется с основанием рассматриваемого твердого тела или между основаниями в случае твердого вещества Bi. An икосаэдр таким образом можно описать как гиродлинная пятиугольная бипирамида.
Дополненный указывает на другой многогранник, а именно на пирамида или же купол, соединяется с одной или несколькими гранями рассматриваемого твердого тела.
Уменьшено указывает, что пирамида или купол удалены с одной или нескольких граней рассматриваемого твердого тела.
Gyrate указывает, что купол, установленный на рассматриваемом твердом теле или представленный в нем, повернут так, что разные края совпадают, как в разнице между орто- и гиробикуполами.

Последние три операции - увеличение, уменьшение, и вращение - может выполняться несколько раз для некоторых крупных твердых тел. Би- & Три- обозначают двойную и тройную операцию соответственно. Например, бигират solid имеет два повернутых купола, а уменьшился в три раза solid имеет три удаленных пирамиды или купола.

В некоторых крупных твердых телах различают твердые тела, у которых измененные грани параллельны, и твердые тела, у которых измененные грани наклонены. Пара- указывает на первое, что рассматриваемое твердое тело изменило параллельные грани, и Мета- последние, изменили косые грани. Например, парабиаугментированный solid было увеличено две параллельные грани, а метабигират solid имеет две наклонные грани, повернутые по спирали.

Последние несколько тел Джонсона имеют имена, основанные на определенных комплексах многоугольников, из которых они собраны. Эти имена определены Джонсоном.^[2]со следующей номенклатурой:

А луна представляет собой комплекс из двух треугольников, прикрепленных к противоположным сторонам квадрата.
Spheno- указывает на клиновидный комплекс, образованный двумя соседними лунками. Дисфено- указывает на два таких комплекса.
Hebespheno- указывает на тупой комплекс двух лунок, разделенных третьей луной.
Корона представляет собой коронообразный комплекс из восьми треугольников.
Мегакорона представляет собой более крупный короноподобный комплекс из 12 треугольников.
Суффикс -цингулум обозначает пояс из 12 треугольников.

Перечисление

Пирамиды, купола и ротонды

Первые 6 тел Джонсона представляют собой пирамиды, купола или ротонды с не более чем 5 боковыми гранями. Пирамиды и купола с 6 или более боковыми гранями компланарны и, следовательно, не являются телами Джонсона.

Пирамиды

Первые два тела Джонсона, J1 и J2, являются пирамиды. В треугольная пирамида регулярный тетраэдр, так что это не твердое тело Джонсона. Они представляют собой сечения правильных многогранников.

Обычный	J1	J2
Треугольная пирамида (Тетраэдр)	Квадратная пирамида	Пятиугольная пирамида


Связанные правильные многогранники
Тетраэдр	Октаэдр	Икосаэдр

Купола и ротонда

Следующие четыре тела Джонсона - это три купола и один ротонда. Они представляют собой сечения однородных многогранников.

Купол				Ротонда
Униформа	J3	J4	J5	J6
Fastigium (Дигональный купол) (Треугольная призма)	Треугольный купол	Квадратный купол	Пятиугольный купол	Пятиугольная ротонда


Связанные однородные многогранники
	Кубооктаэдр	Ромбокубооктаэдр	Ромбикосододекаэдр	Икосододекаэдр

Модифицированные пирамиды

Твердые тела Джонсона с 7 по 17 являются производными пирамид.

Удлиненные и гиродлинные пирамиды

В гиродлинной треугольной пирамиде три пары соседних треугольников компланарны и образуют неквадратные ромбы, поэтому это не твердое тело Джонсона.

Удлиненные пирамиды			Гиро-удлиненные пирамиды
J7	J8	J9	Копланарный	J10	J11
Удлиненная треугольная пирамида	Удлиненная квадратная пирамида	Пятиугольная удлиненная пирамида	Гиро-удлиненная треугольная пирамида (уменьшенный треугольный трапецоэдр)	Гиро-удлиненная квадратная пирамида	Гиро-удлиненная пятиугольная пирамида


Дополнен из многогранников
тетраэдр треугольная призма	квадратная пирамида куб	пятиугольная пирамида пятиугольная призма	тетраэдр октаэдр	квадратная пирамида квадратная антипризма	пятиугольная пирамида пятиугольная антипризма

Бипирамиды

В квадратная бипирамида регулярный октаэдр, в то время как гиродлинная пятиугольная бипирамида регулярный икосаэдр, поэтому они не являются телами Джонсона. В гиродлинной треугольной бипирамиде шесть пар соседних треугольников компланарны и образуют неквадратные ромбы, так что это также не твердое тело Джонсона.

Бипирамиды			Удлиненные бипирамиды			Гиро-удлиненные бипирамиды
J12	Обычный	J13	J14	J15	J16	Копланарный	J17	Обычный
Треугольная бипирамида	Квадратная бипирамида (октаэдр)	Пятиугольная бипирамида	Удлиненная треугольная бипирамида	Удлиненная квадратная бипирамида	Удлиненная пятиугольная бипирамида	Гироудлиненная треугольная бипирамида (треугольный трапецоэдр)	Гиро-удлиненная квадратная бипирамида	Гиро-удлиненная пятиугольная бипирамида (икосаэдр)


Дополнен из многогранников
тетраэдр	квадратная пирамида	пятиугольная пирамида	тетраэдр треугольная призма	квадратная пирамида куб	пятиугольная пирамида пятиугольная призма	тетраэдр Октаэдр	квадратная пирамида квадратная антипризма	пятиугольная пирамида пятиугольная антипризма

Измененные купола и ротонды

Твердые тела Джонсона 18–48 происходят от куполов и ротондов.

Вытянутые и гировидные купола и ротонды.

Вытянутый купол				Удлиненная ротонда	Гиро-удлиненный купол				Гиро-удлиненная ротонда
Копланарный	J18	J19	J20	J21	Вогнутый	J22	J23	J24	J25
Удлиненный фастигиум	Вытянутый треугольный купол	Вытянутый квадратный купол	Вытянутый пятиугольный купол	Удлиненная пятиугольная ротонда	Гиро-удлиненный фастигиум	Гиро-удлиненный треугольный купол	Гиро-удлиненный квадратный купол	Гировидный пятиугольный купол	Гиро-удлиненная пятиугольная ротонда


Дополнен из многогранников
Квадратная призма Треугольная призма	Гексагональная призма Треугольный купол	Восьмиугольная призма Квадратный купол	Десятиугольная призма Пятиугольный купол	Десятиугольная призма Пятиугольная ротонда	квадратная антипризма Треугольная призма	Шестиугольная антипризма Треугольный купол	Восьмиугольная антипризма Квадратный купол	Десятиугольная антипризма Пятиугольный купол	Десятиугольная антипризма Пятиугольная ротонда

Bicupolae

Треугольная гиробикупола - это Архимедово твердое тело (в этом случае кубооктаэдр), так что это не твердое тело Джонсона.

Ортобикупола				Гиробикупола
Копланарный	J27	J28	J30	J26	Полурегулярный	J29	J31
Ортобифастигиум	Ортобикупола треугольная	Квадрат ортобикупола	Пятиугольная ортобикупола	Gyrobifastigium	Гиробикупола треугольная (кубооктаэдр)	Гиробикупола квадратная	Пятиугольная гиробикупола


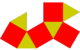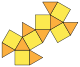Дополнен многогранником
Треугольная призма	Треугольный купол	Квадратный купол	Пятиугольный купол	Треугольная призма	Треугольный купол	Квадратный купол	Пятиугольный купол

Купола-ротонды и биротонды

Пятиугольная гиробиротонда - это Архимедово твердое тело (в этом случае икосододекаэдр), так что это не твердое тело Джонсона.

Купол-ротонда		Биротунда
J32	J33	J34	Полурегулярный
Пятиугольная ортокуполаротонда	Пятиугольная гирокуполаротонда	Пятиугольная ортобиротонда	Пятиугольная гиробиротонда (икосододекаэдр)


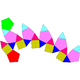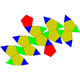Дополнен из многогранников
Пятиугольный купол Пятиугольная ротонда		Пятиугольная ротонда

Удлиненные двуполые

Ортобикупола удлиненной формы квадратная - это Архимедово твердое тело (в этом случае ромбокубооктаэдр), так что это не твердое тело Джонсона.

Ортобикупола удлиненная				Гиробикупола удлиненная
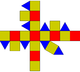
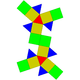
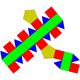
Копланарный	J35	Полурегулярный	J38	Копланарный	J36	J37	J39
Ортобифастигиум удлиненной формы	Ортобикупола удлиненно-треугольной формы	Ортобикупола удлиненная квадратная (ромбокубооктаэдр)	Ортобикупола удлиненная пятиугольная	Гиробифастигий удлиненный	Гиробикупола удлиненной треугольной формы	Гиробикупола удлиненная квадратная	Гиробикупола удлиненная пятиугольная


Дополнен из многогранников
Квадратная призма Треугольная призма	Гексагональная призма Треугольный купол	Восьмиугольная призма Квадратный купол	Десятиугольная призма Пятиугольный купол	Квадратная призма Треугольная призма	Гексагональная призма Треугольный купол	Восьмиугольная призма Квадратный купол	Десятиугольная призма Пятиугольный купол

Вытянутые купола-ротонды и биротонды

Вытянутый купол-ротонда		Удлиненная биротонда
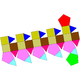
J40	J41	J42	J43
Пятиугольная удлиненная ортокуполаротонда	Удлиненная пятиугольная гирокуполаротонда	Удлиненная пятиугольная ортобиротонда	Удлиненная пятиугольная гиробиротонда


Дополнен из многогранников
Десятиугольная призма Пятиугольный купол Пятиугольная ротонда		Десятиугольная призма Пятиугольная ротонда

Гироудлиненные двупольные, купола-ротонда и биротонда

Эти твердые вещества Джонсона имеют 2 хиральные формы.

Гиро-удлиненная двуполая				Гировидный купол-ротонда	Гироудлиненная биротонда
Вогнутый	J44	J45	J46	J47	J48
Гиро-удлиненный бифастигий	Гиро-удлиненная треугольная двуправая	Гиро-удлиненная квадратная двуправая	Гиро-удлиненная пятиугольная двуправая	Гиро-удлиненная пятиугольная куполаротонда	Гиро-удлиненная пятиугольная биротонда


Дополнен из многогранников
Треугольная призма Квадратная антипризма	Треугольный купол Шестиугольная антипризма	Квадратный купол Восьмиугольная антипризма	Пятиугольный купол Десятиугольная антипризма	Пятиугольный купол Пятиугольная ротонда Десятиугольная антипризма	Пятиугольная ротонда Десятиугольная антипризма

Увеличенные призмы

Твердые тела Джонсона с 49 по 57 построены путем добавления сторон призм квадратными пирамидами.

Увеличенные треугольные призмы			Увеличенные пятиугольные призмы		Увеличенные шестиугольные призмы
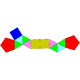
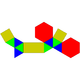
J49	J50	J51	J52	J53	J54	J55	J56	J57
Расширенная треугольная призма	Двойная треугольная призма	Трехгранная треугольная призма	Расширенная пятиугольная призма	Двухугольная пятиугольная призма	Расширенная шестиугольная призма	Парабиаугментированная шестиугольная призма	Метабиаугментированная шестиугольная призма	Трехгранная шестиугольная призма


Дополнен из многогранников
Треугольная призма Квадратная пирамида			Пятиугольная призма Квадратная пирамида		Гексагональная призма Квадратная пирамида

Модифицированные Платоновы тела

Твердые тела Джонсона с 58 по 64 строятся путем увеличения или уменьшения количества Платоновых тел.

Дополненные додекаэдры

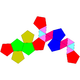
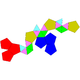
J58	J59	J60	J61
Дополненный додекаэдр	Парабиаугментированный додекаэдр	Метабиауглеродный додекаэдр	Триаугментированный додекаэдр


Дополнен из многогранников
Додекаэдр и пятиугольная пирамида

Уменьшенные и увеличенные уменьшенные икосаэдры

Уменьшенный икосаэдр				Увеличенный трехуменьшенный икосаэдр
J11 (Повторяется)	Униформа	J62	J63	J64
Уменьшенный икосаэдр (Гиро-удлиненная пятиугольная пирамида)	Парабидоусиленный икосаэдр (Пятиугольная антипризма)	Метабидоуменьшенный икосаэдр	Треугольный икосаэдр	Увеличенный трехуменьшенный икосаэдр

Модифицированные архимедовы тела

Твердые тела Джонсона 65-83 построены путем увеличения, уменьшения или вращения архимедовых тел.

Дополненные архимедовы тела

Увеличенный усеченный тетраэдр	Дополненные усеченные кубики		Дополненные усеченные додекаэдры
J65	J66	J67	J68	J69	J70	J71
Увеличенный усеченный тетраэдр	Увеличенный усеченный куб	Усеченный двуугловой куб	Увеличенный усеченный додекаэдр	Парабиаугментированный усеченный додекаэдр	Усеченный додекаэдр с метабиаугментацией	Триаугментированный усеченный додекаэдр


Дополнен из многогранников
усеченный тетраэдр треугольный купол	усеченный куб квадратный купол		усеченный додекаэдр пятиугольный купол

Гиратные и уменьшенные ромбикосододекаэдры

Гиратные ромбикосододекаэдры
J72	J73	J74	J75
Гират ромбикосододекаэдр	Парабигиратный ромбикосододекаэдр	Метабигиратный ромбикосододекаэдр	Тригиратный ромбоикосододекаэдр


Уменьшенные ромбикосододекаэдры
J76	J80	J81	J83
Уменьшенный ромбоикосододекаэдр	Парабидоусиленный ромбоикосододекаэдр	Метабидоуменьшенный ромбикосододекаэдр	Трехкоординатный ромбоикосододекаэдр


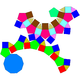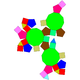Гиратные уменьшенные ромбикосододекаэдры
J77	J78	J79	J82
Парагиратный уменьшенный ромбикосододекаэдр	Метагират уменьшенный ромбикосододекаэдр	Бигират уменьшенный ромбикосододекаэдр	Гиратный двумерный ромбикосододекаэдр

J37 также может появиться здесь как дубликат (это круговой ромбокубооктаэдр).

Другие вращающиеся и уменьшенные архимедовы тела

Другие архимедовы твердые тела могут вращаться и уменьшаться, но все они приводят к ранее подсчитанным твердым телам.

J27	J3	J34	J6	J37	J19
Гиратный кубооктаэдр (треугольная ортобикупола)	Уменьшенный кубооктаэдр (треугольный купол)	Гират икосододекаэдр (пятиугольная ортобиротонда)	Уменьшенный икосододекаэдр (пятиугольная ротонда)	Гиратный ромбокубооктаэдр (удлиненная квадратная гиробикупола)	Уменьшенный ромбокубооктаэдр (удлиненный квадратный купол)


Гирированные или уменьшенные из многогранников
Кубооктаэдр		Икосододекаэдр		Ромбокубооктаэдр

Элементарные твердые тела

Твердые вещества Джонсона с 84 по 92 не являются производными от манипуляций "вырезать и вставить" униформа твердые тела.

Курносые антипризмы

В пренебрежительно антипризмы можно построить как чередование усеченной антипризмы. Гиробиантикуполы - еще одна конструкция курносых антипризм. Только курносые антипризмы с не более чем 4 сторонами могут быть построены из правильных многоугольников. Курносая треугольная антипризма - это правильная икосаэдр, так что это не твердое тело Джонсона.

J84	Обычный	J85
Курносый дисфеноид сс {2,4}	Икосаэдр сс {2,6}	Плоская квадратная антипризма сс {2,8}
Дигональные гиробиантикуполы	Гиробиантикупола треугольная	Квадратная гиробиантикупола

Другие

J86	J87	J88
Sphenocorona	Увеличенная сфенокорона	Sphenomegacorona


J89	J90	J91	J92
Hebesphenomegacorona	Дисфеноцингулум	Bilunabirotunda	Гебешфеноротунда треугольная

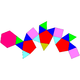Классификация по типам лиц

Треугольные тела Джонсона

Пять твердых тел Джонсона дельтаэдры, со всеми гранями равностороннего треугольника:

J12 Треугольная бипирамида J13 Пятиугольная бипирамида J17 Гиро-удлиненная квадратная бипирамида	J51 Трехгранная треугольная призма J84 Курносый дисфеноид

Треугольные и квадратные тела Джонсона

Двадцать четыре тела Джонсона имеют только треугольные или квадратные грани:

J1 Квадратная пирамида J7 Удлиненная треугольная пирамида J8 Удлиненная квадратная пирамида J10 Гиро-удлиненная квадратная пирамида J14 Удлиненная треугольная бипирамида J15 Удлиненная квадратная бипирамида J16 Удлиненная пятиугольная бипирамида J26 Gyrobifastigium	J27 Ортобикупола треугольная J28 Квадрат ортобикупола J29 Гиробикупола квадратная J35 Ортобикупола удлиненно-треугольной формы J36 Гиробикупола удлиненной треугольной формы J37 Гиробикупола удлиненная квадратная J44 Гиро-удлиненная треугольная двуправая J45 Гиро-удлиненная квадратная двуправая	J49 Расширенная треугольная призма J50 Двойная треугольная призма J85 Плоская квадратная антипризма J86 Sphenocorona J87 Увеличенная сфенокорона J88 Sphenomegacorona J89 Hebesphenomegacorona J90 Дисфеноцингулум

Треугольные и пятиугольные тела Джонсона

Одиннадцать тел Джонсона имеют только треугольные и пятиугольные грани:

Треугольные, квадратные и пятиугольные тела Джонсона

Двадцать тел Джонсона имеют только треугольные, квадратные и пятиугольные грани:

J09 Пятиугольная удлиненная пирамида J30 Пятиугольная ортобикупола J31 Пятиугольная гиробикупола J32 Пятиугольная ортокуполаротонда J33 Пятиугольная гирокуполаротонда J38 Ортобикупола удлиненная пятиугольная J39 Гиробикупола удлиненная пятиугольная J40 Пятиугольная удлиненная ортокуполаротонда J41 Удлиненная пятиугольная гирокуполаротонда J42 Удлиненная пятиугольная ортобиротонда	J43 Удлиненная пятиугольная гиробиротонда J46 Гиро-удлиненная пятиугольная двуправая J47 Гиро-удлиненная пятиугольная куполаротонда J52 Расширенная пятиугольная призма J53 Двухугольная пятиугольная призма J72 Гиратный ромбикосододекаэдр J73 Парабигиратный ромбикосододекаэдр J74 Метабигиратный ромбикосододекаэдр J75 Тригиратный ромбоикосододекаэдр J91 Bilunabirotunda

Треугольные, квадратные и шестиугольные тела Джонсона

Восемь тел Джонсона имеют только треугольные, квадратные и шестиугольные грани:

J3 Треугольный купол J18 Вытянутый треугольный купол J22 Гиро-удлиненный треугольный купол J54 Расширенная шестиугольная призма	J55 Парабиаугментированная шестиугольная призма J56 Метабиауглеродная шестиугольная призма J57 Трехгранная шестиугольная призма J65 Увеличенный усеченный тетраэдр

Треугольные, квадратные и восьмиугольные тела Джонсона

Пять тел Джонсона имеют только треугольные, квадратные и восьмиугольные грани:

J4 Квадратный купол J19 Вытянутый квадратный купол J23 Гиро-удлиненный квадратный купол	J66 Увеличенный усеченный куб J67 Усеченный двуугловой куб

Треугольники, пятиугольники и десятиугольные тела Джонсона

Два тела Джонсона имеют только треугольные, пятиугольные и десятиугольные грани:

J06 Пятиугольная ротонда J25 Гиро-удлиненная пятиугольная ротонда

Треугольники, квадраты, пятиугольники и шестиугольники с гранями тела Джонсона

Только одно тело Джонсона имеет треугольные, квадратные, пятиугольные и шестиугольные грани:

J92 Гебешфеноротунда треугольная

Треугольники, квадраты, пятиугольники и десятиугольные тела Джонсона

Шестнадцать тел Джонсона имеют только треугольник, квадрат, пятиугольник и десятиугольник:

J05 Пятиугольный купол J20 Вытянутый пятиугольный купол J21 Удлиненная пятиугольная ротонда J24 Гировидный пятиугольный купол J68 Дополненный усеченный додекаэдр J69 Парабиаугментированный усеченный додекаэдр J70 Усеченный додекаэдр с метабиаугментацией J71 Триаугментированный усеченный додекаэдр	J76 Уменьшенный ромбикосододекаэдр J77 Парагиратный уменьшенный ромбикосододекаэдр J78 Метагират уменьшенный ромбикосододекаэдр J79 Бигират уменьшенный ромбикосододекаэдр J80 Парабидоусиленный ромбоикосододекаэдр J81 Метабидоуменьшенный ромбикосододекаэдр J82 Гират двумерный ромбикосододекаэдр J83 Трехкоординатный ромбоикосододекаэдр

Объявляемые твердые тела Джонсона

25 тел Джонсона имеют вершины, которые существуют на поверхности сфера: 1–6,11,19,27,34,37,62,63,72–83. Все они могут быть связаны с правильным или однородным многогранником путем вращения, уменьшения или рассечения.^[3]

Октаэдр	Кубооктаэдр		Ромбокубооктаэдр
J1	J3	J27	J4	J19	J37

Икосаэдр				Икосододекаэдр
J2	J11	J62	J63	J6	J34

Ромбикосододекаэдр
J5	J72	J73	J74	J75	J76	J77
J5	J78	J79	J80	J81	J82	J83

Смотрите также

внешняя ссылка

Ганьон, Сильвен (1982). "Выпуклые полиэдры aux Face Régulières" [Выпуклые многогранники с правильными гранями] (PDF). Структурная топология (6): 83–95.
Бумажные модели многогранников Много ссылок
Джонсон Солидс Джорджа У. Харта.
Изображения всех 92 твердых тел по категориям на одной странице
Вайсштейн, Эрик В. "Джонсон Солид". MathWorld.
VRML-модели Johnson Solids Джим Макнил
VRML-модели Johnson Solids Владимир Булатов
CRF проект открытия полихоры попытки обнаружить CRF полихора, обобщение тел Джонсона на 4-мерное пространство
https://levskaya.github.io/polyhedronisme/ генератор многогранников и Конвей операции применительно к ним, включая твердые тела Джонсона.

[1] GWH. «Псевдо ромбокубооктаэдры». www.georgehart.com. Получено 17 апреля 2018.

[2] Джордж Харт (цитирует Джонсона) (1996). "Джонсон Солидс". Виртуальные многогранники. Получено 5 февраля 2014.

[3] Клитцинг, доктор Ричард. «Джонсон солидс и др.». bendwavy.org. Получено 17 апреля 2018.

[1]

[2]

[3]

v т е Твердые тела Джонсона
Пирамиды, купола и ротонды	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Изменено пирамиды	удлиненная треугольная пирамида удлиненная квадратная пирамида удлиненная пятиугольная пирамида гировидная квадратная пирамида гировидная пятиугольная пирамида треугольная бипирамида квадратная бипирамида пятиугольная бипирамида удлиненная треугольная бипирамида удлиненная квадратная бипирамида удлиненная пятиугольная бипирамида гиродлинная квадратная бипирамида
Изменено купола и ротонды	удлиненный треугольный купол удлиненный квадратный купол удлиненный пятиугольный купол удлиненная пятиугольная ротонда гировидный треугольный купол гировидный квадратный купол гиродлинная пятиугольная куполка гировидная пятиугольная ротонда гиробифастигий треугольная ортобикупола квадратный ортобикупола квадратная гиробикупола пятиугольная ортобикупола пятиугольная гиробикупола пятиугольная орто-куполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда ортобикупола удлиненно-треугольной формы удлиненно-треугольная гиробикупола удлиненная квадратная гиробикупола удлиненные пятиугольные ортобикуполы удлиненная пятиугольная гиробикупола удлиненная пятиугольная орто-куполаротонда удлиненная пятиугольная гирокуполаротонда удлиненная пятиугольная ортобиротонда удлиненная пятиугольная гиробиротонда гиродлинно-треугольная двуполая гиродлинная квадратная двуполая гировидная пятиугольная двуполая гировидная пятиугольная куполаротонда гировидная пятиугольная биротонда
Дополненный призмы	увеличенная треугольная призма двуугловая треугольная призма трехугольная призма увеличенная пятиугольная призма двуугловая пятиугольная призма увеличенная шестиугольная призма парабиаугментированная шестиугольная призма метабиауглеродная шестиугольная призма трехкратная шестиугольная призма
Изменено Платоновы тела	расширенный додекаэдр парабиаугментированный додекаэдр метабиауглеродный додекаэдр триаугментированный додекаэдр икосаэдр с уменьшенным метабидом трехуменьшенный икосаэдр трижды уменьшенный икосаэдр
Изменено Архимедовы тела	расширенный усеченный тетраэдр увеличенный усеченный куб двунаправленный усеченный куб дополненный усеченный додекаэдр парабиаугментированный усеченный додекаэдр усеченный метабиауглеродный додекаэдр усеченный додекаэдр спиральный ромбикосододекаэдр парабигиратный ромбикосододекаэдр метабигиратный ромбикосододекаэдр трехгранный ромбикосододекаэдр уменьшенный ромбикосододекаэдр парагират уменьшенный ромбикосододекаэдр метагират уменьшенный ромбикосододекаэдр бигират уменьшенный ромбикосододекаэдр парабидоусиленный ромбоикосододекаэдр метабидоусиленный ромбикосододекаэдр вращающийся двумерный ромбикосододекаэдр трехкоординатный ромбоикосододекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона увеличенная сфенокорона сфеномегакорона Hebesphenomegacorona дифеноцингулум билунабиротонда треугольная гебесфеноротунда
(Смотрите также Список твердых тел Джонсона, сортируемая таблица)

Navigation