WikiDer > Гиро-удлиненный треугольный купол
| Гиро-удлиненный треугольный купол | |
|---|---|
 | |
| Тип | Джонсон J21 - J22 - J23 |
| Лица | 1 + 3x3 + 6 треугольники 3 квадраты 1 шестиугольник |
| Края | 33 |
| Вершины | 15 |
| Конфигурация вершины | 3(3.4.3.4) 2.3(33.6) 6(34.4) |
| Группа симметрии | C3в |
| Двойной многогранник | - |
| Характеристики | выпуклый |
| Сеть | |
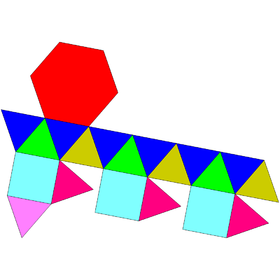 | |
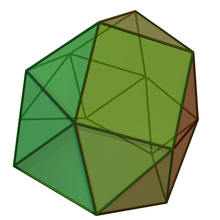
В геометрия, то гировидный треугольный купол один из Твердые тела Джонсона (J22). Его можно построить, прикрепив шестиугольная антипризма к основанию треугольный купол (J3). Это называется «гироудлинением», что означает, что антипризма соединяется с основанием твердого тела или между основаниями более чем одного твердого тела.
Гиро-удлиненный треугольный купол также можно рассматривать как гиродлинно-треугольная двуполая (J44) со снятым одним треугольным куполом. Как все купола, то основание многоугольник имеет в два раза больше сторон, чем верхний (в этом случае нижний многоугольник является шестиугольник потому что верх - это треугольник).
А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.[1]
Формулы
Следующее формулы за объем и площадь поверхности можно использовать, если все лица находятся обычный, с длиной кромки а:[2]
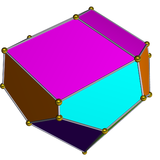
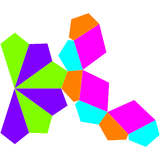
Двойной многогранник
Двойник гировидного треугольного купола имеет 15 граней: 6 воздушных змеев, 3 ромба и 6 пятиугольников.
| Двойной гиродлинно-треугольный купол | Чистая двойная |
|---|---|
 |  |
Рекомендации
- ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР 0185507, Zbl 0132.14603.
- ^ Стивен Вольфрам, "Гиро-удлиненный треугольный купол" из вольфрам Альфа. Проверено 22 июля 2010 года.
внешняя ссылка
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |

