WikiDer > Удлиненная треугольная бипирамида

Удлиненная треугольная бипирамида
Тип	Джонсон J13 - J14 - J15
Лица	6 треугольники 3 квадраты
Края	15
Вершины	8
Конфигурация вершины	2(33) 6(32.42)
Группа симметрии	D3ч, [3,2], (*322)
Группа вращения	D3, [3,2]+, (322)
Двойной многогранник	Двустворчатый треугольный
Характеристики	выпуклый
Сеть

Солидо де Джонсон Джо

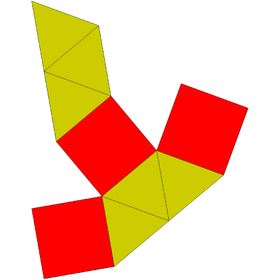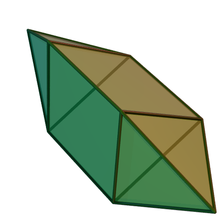
В геометрия, то удлиненно-треугольный бипирамида (или же дипирамида) или же треугольная призма триаки один из Твердые тела Джонсона (J₁₄), выпуклые многогранники чьи лица правильные многоугольники. Как следует из названия, его можно построить, удлинив треугольная бипирамида (J₁₂), вставив треугольная призма между его конгруэнтными половинками.

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 г.^[1]

В ниррозулаАфриканский музыкальный инструмент, сплетенный из полосок листьев растений, выполнен в виде серии удлиненных бипирамид с неравносторонними треугольниками на торцах.^[2]

Формулы

Следующее формулы за объем (${ displaystyle V}$), площадь поверхности (${ displaystyle A}$) и высота (${ displaystyle H}$) можно использовать, если все лица находятся обычный, с длиной кромки а:

${ displaystyle V = ({ frac {1} {12}} (2 { sqrt {2}} + 3 { sqrt {3}})) cdot a ^ {3} приблизительно 0,668715 ... a ^ {3}}$^[3][4]

${ displaystyle A = ({ frac {3} {2}} (2 + { sqrt {3}})) cdot a ^ {2} приблизительно 5.59808 ... a ^ {2}}$^[3][4]

${ displaystyle H = { frac {3 + 2 { sqrt {6}}} {3}} cdot a приблизительно cdot 2.63299 ... a}$^[4]

Двойной многогранник

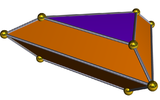
Двойник удлиненной треугольной бипирамиды называется треугольный двустворчатый и имеет 8 граней: 6 трапециевидных и 2 треугольных.

Двойная удлиненная треугольная бипирамида	Чистая двойная

Рекомендации

внешняя ссылка

• Эрик В. Вайсштейн, Удлиненная треугольная бипирамида (Джонсон солид) в MathWorld.

Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. v т е