WikiDer > Плоская квадратная антипризма
| Плоская квадратная антипризма | |
|---|---|
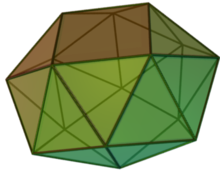 | |
| Тип | Джонсон J84 - J85 - J86 |
| Лица | 8+16 треугольники 2 квадраты |
| Края | 40 |
| Вершины | 16 |
| Конфигурация вершины | 8(35) 8(34.4) |
| Группа симметрии | D4d |
| Двойной многогранник | - |
| Характеристики | выпуклый |
| Сеть | |
 | |
В геометрия, то курносая квадратная антипризма один из Твердые тела Джонсона (J85) .A Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.[1]
Это одно из элементарных твердых тел Джонсона, которое не возникает в результате манипуляций "вырезать и вставить" Платонический и Архимедов твердых тел, хотя это родственник икосаэдр имеющий четырехкратную симметрию вместо троичной.
Строительство
В курносая квадратная антипризма построен, как следует из названия, квадратная антипризма который пренебрежительно, и представлен как ss {2,8}, где s {2,8} как квадратная антипризма.[2] Его можно построить в Обозначения многогранника Конвея как sY4 (курносая квадратная пирамида).[3]
Его также можно построить в виде квадрата gyrobianticupolae, соединяя два anticupolae с вращающейся ориентацией.
Декартовы координаты
Позволять k ≈ 0,82354 - положительный корень кубический многочлен
Кроме того, пусть час ≈ 1,35374 определяется как
Потом, Декартовы координаты курносой квадратной антипризмы с длиной ребра 2 задаются объединением орбит точек
под действием группа генерируется вращением вокруг оси z на 90 ° и вращением на 180 ° вокруг прямой линии, перпендикулярной оси z и составляющей угол 22,5 ° с осью x.[4]
Затем мы можем вычислить площадь поверхности курносого квадрата с длиной ребра а в качестве
и это объем в качестве
куда ξ ≈ 3.60122 - наибольший действительный корень многочлена
Курносые антипризмы
Построенный аналогично, сс {2,6} является курносая треугольная антипризма (более низкая симметрия октаэдр), и результат как регулярный икосаэдр. А курносая пятиугольная антипризма, ss {2,10} или выше п-антипризмы могут быть построены аналогично, но не как выпуклый многогранник с равносторонними треугольниками. Предыдущее твердое тело Джонсона, курносый дисфеноид также конструктивно подходит как ss {2,4}, но необходимо сохранить два вырожденных двуугольный лица (нарисованные красным) в дигональная антипризма.
| Симметрия | D2d, [2+,4], (2*2) | D3D, [2+,6], (2*3) | D4d, [2+,8], (2*4) | D5d, [2+,10], (2*5) |
|---|---|---|---|---|
| Антипризмы |  с {2,4} A2 (v: 4; e: 8; f: 6) |  с {2,6} A3 (v: 6; e: 12; f: 8) |  с {2,8} A4 (v: 8; e: 16; f: 10) |  с {2,10} A5 (v: 10; e: 20; f: 12) |
| Усеченный антипризмы |  ts {2,4} tA2 (v: 16; e: 24; f: 10) |  ts {2,6} tA3 (v: 24; e: 36; f: 14) |  ts {2,8} tA4 (v: 32; e: 48; f: 18) |  тс {2,10} tA5 (v: 40; e: 60; f: 22) |
| Симметрия | D2, [2,2]+, (222) | D3, [3,2]+, (322) | D4, [4,2]+, (422) | D5, [5,2]+, (522) |
| Курносый антипризмы | J84 | Икосаэдр | J85 | Вогнутый |
| sY3 = HtA3 | sY4 = HtA4 | sY5 = HtA5 | ||
 сс {2,4} (v: 8; e: 20; f: 14) |  сс {2,6} (v: 12; e: 30; f: 20) |  сс {2,8} (v: 16; e: 40; f: 26) | сс {2,10} (v: 20; e: 50; f: 32) |
Рекомендации
- ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР 0185507, Zbl 0132.14603.
- ^ Курносые антипризмы
- ^ https://levskaya.github.io/polyhedronisme/?recipe=C100sY4
- ^ Тимофеенко, А. В. (2009). «Неплатоновы и неархимедовы несоставные многогранники». Журнал математических наук. 162 (5): 725.
- ^ Wolfram Research, Inc. (2020). "Wolfram | Alpha Knowledgebase". Шампейн, Иллинойс.
Цитировать журнал требуетPolyhedronData [{"Johnson", 85}, "SurfaceArea"]| журнал =(помощь) - ^ Wolfram Research, Inc. (2020). "Wolfram | Alpha Knowledgebase". Шампейн, Иллинойс.
Цитировать журнал требуетMinimalPolynomial [PolyhedronData [{"Джонсон", 85}, "Объем"], x]| журнал =(помощь)
внешняя ссылка
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |






