WikiDer > Пятиугольная антипризма
| Равномерная пятиугольная антипризма | |
|---|---|
 | |
| Тип | Призматический однородный многогранник |
| Элементы | F = 12, E = 20 V = 10 (χ = 2) |
| Лица по сторонам | 10{3}+2{5} |
| Символ Шлефли | с {2,10} ср {2,5} |
| Символ Wythoff | | 2 2 5 |
| Диаграмма Кокстера | |
| Группа симметрии | D5d, [2+, 10], (2 * 5), порядок 20 |
| Группа вращения | D5, [5,2]+, (522), порядок 10 |
| Рекомендации | U77 (с) |
| Двойной | Пятиугольный трапецииэдр |
| Характеристики | выпуклый |
 Фигура вершины 3.3.3.5 | |
В геометрия, то пятиугольная антипризма является третьим в бесконечном наборе антипризмы образованный четной последовательностью сторон треугольника, закрытых двумя крышками многоугольника. Он состоит из двух пятиугольники соединены друг с другом кольцом из 10 треугольники всего 12 граней. Следовательно, это нерегулярный додекаэдр.
Геометрия
Если все грани пятиугольной антипризмы правильные, это полуправильный многогранник. Его также можно рассматривать как парабидимулированный икосаэдр, форма, образованная удалением двух пятиугольные пирамиды из правильный икосаэдр оставив две несмежные пятиугольные грани; родственная форма, икосаэдр с уменьшенным метабидом (один из Твердые тела Джонсона), аналогично образует икосаэдр путем удаления двух пирамид, но его пятиугольные грани примыкают друг к другу. Две пятиугольные грани любой формы можно дополнить пирамидами, чтобы сформировать икосаэдр.
Связь с многогранниками
Пятиугольная антипризма возникает как составной элемент в некоторых многомерных многогранники. Два кольца из 10 пятиугольных антипризм ограничивают гиперповерхность четырехмерного великая антипризма. Если эти антипризмы дополнить пирамидами пятиугольной призмы и соединить кольцами по 5 тетраэдров в каждом, то 600 ячеек получается.
Смотрите также
В пятиугольная антипризма можно обрезать и чередовать, чтобы сформировать пренебрежительная антипризма:
| Антипризма A5 | Усеченный tA5 | Альтернативный htA5 |
|---|---|---|
 | 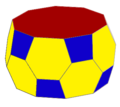 |  |
| с {2,10} | тс {2,10} | сс {2,10} |
| v: 10; е: 20; ж: 12 | v: 40; е: 60; ж: 22 | v: 20; е: 50; ж: 32 |
| Семья униформы п-гональный антипризмы | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника | ... | Апейрогональная антипризма | ||||||||||||
| Сферическое мозаичное изображение | Плоское мозаичное изображение | |||||||||||||
| Конфигурация вершины п.3.3.3 | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 | |
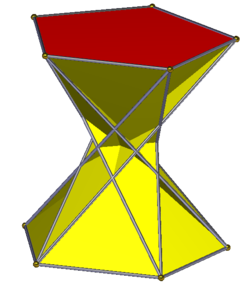
Скрещенная антипризма
Перекрещенная пятиугольная антипризма топологически идентична пятиугольная антипризма, хотя его нельзя сделать единообразным. Стороны равнобедренные треугольники. Он имеет d5d симметрия, порядок 10. Его конфигурация вершины составляет 3.3 / 2.3.5, с одним ретроградным треугольником и его расположение вершин это то же самое, что и пятиугольная призма.
внешняя ссылка
- Вайсштейн, Эрик В. «Антипризма». MathWorld.
- [1]
- Пятиугольная антипризма: интерактивная модель многогранника
- Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
- VRML модель
- Обозначение Конвея для многогранников Попробуйте: «А5»
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |