WikiDer > Ромбикосододекаэдр
| Ромбикосододекаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 62, E = 120, V = 60 (χ = 2) |
| Лица по сторонам | 20{3}+30{4}+12{5} |
| Обозначение Конвея | eD или aaD |
| Символы Шлефли | rr {5,3} или |
| т0,2{5,3} | |
| Символ Wythoff | 3 5 | 2 |
| Диаграмма Кокстера | |
| Группа симметрии | ячас, H3, [5,3], (* 532), заказ 120 |
| Группа вращения | я, [5,3]+, (532), заказ 60 |
| Двугранный угол | 3-4: 159°05′41″ (159.09°) 4-5: 148°16′57″ (148.28°) |
| Рекомендации | U27, C30, W14 |
| Характеристики | Полурегулярный выпуклый |
 Цветные лица |  3.4.5.4 (Фигура вершины) |
 Дельтоидальный гексеконтаэдр (двойственный многогранник) |  Сеть |
В геометрия, то ромбикосододекаэдр, является Архимедово твердое тело, один из тринадцати выпуклый изогональный непризматические твердые тела, состоящие из двух или более типов правильный многоугольник лица.
Имеет 20 обычных треугольный лица, 30 квадрат лиц, 12 обычных пятиугольник лица, 60 вершины, и 120 края.
Имена
Иоганн Кеплер в Harmonices Mundi (1618) назвал этот многогранник a ромбикосододекаэдр, сокращение от усеченный икосододекаэдрический ромб, с икосододекаэдрический ромб быть его именем для ромбический триаконтаэдр.[1] Ромбический триаконтаэдр может быть усечен по-разному. топологический ромбикосододекаэдр: в основном его исправление (слева), тот, который создает однородное твердое тело (в центре), и выпрямление двойного икосододекаэдр (справа), который является ядром двойное соединение.
Его также можно назвать расширенный или же канеллированный додекаэдр или икосаэдр, от операций усечения на любом равномерный многогранник.
Геометрические отношения
если ты расширять ан икосаэдр перемещая лица от источник нужное количество, не меняя ориентации или размера лиц, и сделайте то же самое с его двойной додекаэдр, и залатав квадратные дыры в результате, получится ромбоикосододекаэдр. Следовательно, у него такое же количество треугольников, что и у икосаэдра, и такое же количество пятиугольников, как у додекаэдра, с квадратом на каждом ребре.
В качестве альтернативы, если вы расширять каждый из пяти кубиков, перемещая грани от источник на нужную величину и вращая каждую из пяти на 72 ° вокруг так, чтобы они были равноудалены друг от друга, без изменения ориентации или размера граней, и заделав в результате пятиугольные и треугольные отверстия, вы получите ромбикосододекаэдр. Следовательно, он имеет такое же количество треугольников, что и икосаэдр, и такое же количество пятиугольников, как додекаэдр, с квадратом на каждом краю каждого из них.
Ромбикосододекаэдр имеет общее расположение вершин с малый звездчатый усеченный додекаэдр, и с единообразными соединениями шести или двенадцати пентаграммические призмы.
В Zometool наборы для изготовления геодезические купола и другие многогранники используют шарики с прорезями в качестве соединителей. Шары представляют собой «расширенные» ромбикосододекаэдры, в которых квадраты заменены прямоугольниками. Расширение выбрано так, чтобы получившиеся прямоугольники были золотые прямоугольники.
Двенадцать из 92 Твердые тела Джонсона происходят от ромбикосододекаэдра, четыре из них вращением одного или нескольких пятиугольные купола: the вращаться, парабигират, метабигират, и тригиратный ромбикосододекаэдр. Еще восемь можно построить, удалив до трех куполов, иногда также вращая один или несколько других куполов.
Декартовы координаты
Декартовы координаты для вершин ромбикосододекаэдра с длиной ребра 2 с центром в начале координат все даже перестановки из:[2]
- (±1, ±1, ±φ3),
- (±φ2, ±φ, ±2φ),
- (±(2+φ), 0, ±φ2),
куда φ = 1 + √5/2 это Золотое сечение. Следовательно, описанный радиус этого ромбикосододекаэдра равен общему расстоянию этих точек от начала координат, а именно √φ6+2 = √8φ + 7 для длины кромки 2. Для единичной длины кромки R нужно уменьшить вдвое, что дает
- р = √8φ+7/2 = √11+4√5/2 ≈ 2.233.
Ортогональные проекции
В ромбикосододекаэдр имеет шесть специальных ортогональные проекции, с центром, на вершине, на двух типах ребер и трех типах граней: треугольниках, квадратах и пятиугольниках. Последние два соответствуют букве A2 и H2 Самолеты Кокстера.
| В центре | Вершина | Край 3-4 | Край 5-4 | Лицо Квадрат | Лицо Треугольник | Лицо Пентагон |
|---|---|---|---|---|---|---|
| Твердый |  |  |  | |||
| Каркас |  |  |  |  |  |  |
| Проективный симметрия | [2] | [2] | [2] | [2] | [6] | [10] |
| Двойной изображение |  |  |  |  |  |  |
Сферическая черепица
Ромбикосододекаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
 |  Пентагон-центрированный |  Треугольник-центрированный |  Квадрат-центрированный |
| Ортографическая проекция | Стереографические проекции | ||
|---|---|---|---|
Связанные многогранники
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Мутации симметрии
Этот многогранник топологически связан как часть последовательности канеллированный многогранники с вершинной фигурой (3.4.n.4), которая продолжается как мозаики гиперболическая плоскость. Эти вершинно-транзитивный фигуры имеют (* n32) отражающие симметрия.
| *п32 мутации симметрии расширенных мозаик: 3.4.п.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paracomp. | ||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Фигура |  |  |  |  |  |  |  | |
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Твердые тела Джонсона
Есть 13 связанных Твердые тела Джонсона, 5 по убыванию и 8 с учетом вращения:
J5 | 76 | 80 | 81 | 83 |
72 | 73 | 74 | 75 |
77 | 78 | 79 | 82 |
Расположение вершин
Ромбикосододекаэдр разделяет расположение вершин с тремя невыпуклые равномерные многогранники: the малый звездчатый усеченный додекаэдр, то малый додецикозододекаэдр (имеющий общие треугольные и пятиугольные грани), а малый ромбидодекаэдр (имеющий общие квадратные грани).
Он также разделяет расположение вершин с однородные соединения из шесть или же двенадцать пентаграммических призм.
 Ромбикосододекаэдр |  Малый додецикосододекаэдр |  Малый ромбидодекаэдр |
 Малый звездчатый усеченный додекаэдр |  Соединение шести пентаграммических призм |  Соединение двенадцати пентаграммических призм |
Ромбикосододекаэдрический граф
| Ромбикосододекаэдрический граф | |
|---|---|
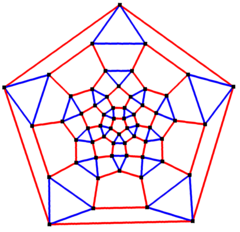 Диаграмма Шлегеля в центре Пентагона | |
| Вершины | 60 |
| Края | 120 |
| Автоморфизмы | 120 |
| Характеристики | Граф четвертого порядка, Гамильтониан, обычный |
| Таблица графиков и параметров | |
в математический поле теория графов, а ромбикосододекаэдрический граф это граф вершин и ребер ромбикосододекаэдра, один из Архимедовы тела. Имеет 60 вершины и 120 ребер, а это график четвертой степени Архимедов граф.[4]

Смотрите также
Примечания
- ^ Гармонии Мира Иоганна Кеплера, Перевод на английский язык с введением и примечаниями Э. Дж. Эйтон, А. М. Дункан, "Дж. В. Филд, 1997, ISBN 0-87169-209-0 (стр.123)
- ^ Вайсштейн, Эрик В. «Икосаэдрическая группа». MathWorld.
- ^ Вайсштейн, Эрик В. "Зомэ". MathWorld.
- ^ Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269
Рекомендации
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN 0-521-55432-2.
- Теория большого взрыва Сезон 8 Эпизод 2 - Решение младшего профессора: представляет этот солидный ответ на импровизированную научную викторину, которую четыре главных героя проводят в квартире Леонарда и Шелдона, а также проиллюстрирован на Чак Лоррес Карточка тщеславия № 461 в конце этого эпизода.
внешняя ссылка
- Эрик В. Вайсштейн, Малый ромбикосододекаэдр (Архимедово твердое тело) в MathWorld.
- Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3o5x - srid".
- Редактируемая сетка для печати ромбикосододекаэдра с интерактивным трехмерным изображением
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников

















































