WikiDer > Гиро-удлиненная пирамида
| Набор гиродлинных пирамид | |
|---|---|
 Пример пятиугольной формы | |
| Лица | 3n треугольники 1 н-угольник |
| Края | 5н |
| Вершины | 2n + 1 |
| Группа симметрии | CNV, [n], (* nn) |
| Группа вращения | Cп, [n]+, (nn) |
| Двойной многогранник | ? |
| Свойства | выпуклый |
В геометрия, то гиродлинные пирамиды (также называется расширенным антипризмы) представляют собой бесконечное множество многогранники, построенный присоединением n-угольного пирамида н-угольному антипризма.
Есть два гиродлинные пирамиды которые Твердые тела Джонсона сделаны из правильных треугольников и квадрата, и пятиугольника. Треугольная и шестиугольная формы могут быть построены с копланарный лица. Другие могут быть построены с учетом равнобедренных треугольников.
Формы
| Образ | имя | Лица |
|---|---|---|
 | Гиро-удлиненная треугольная пирамида (Копланарные лица) | 9 + 1 треугольников |
 | Гиро-удлиненная квадратная пирамида (J10) | 12 треугольников, 1 квадрат |
 | Гиро-удлиненная пятиугольная пирамида (J11) | 15 треугольников, 1 пятиугольник |
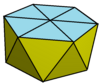 | Гиро-удлиненная шестиугольная пирамида (Копланарные лица) | 18 треугольников, 1 шестиугольник |
Смотрите также
использованная литература
- Норман В. Джонсон, «Выпуклые тела с правильными гранями», Канадский математический журнал, 18, 1966, стр. 169–200. Содержит исходное перечисление 92 твердых тел и гипотезу о том, что других нет.
- Виктор Александрович Залгаллер (1969). Выпуклые многогранники с правильными гранями. Бюро консультантов. Нет ISBN. Первое доказательство того, что тел Джонсона всего 92.
| Эта многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |