WikiDer > Гиро-удлиненный купол

Комплект гиро-удлиненных куполов
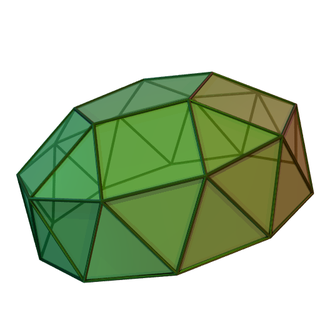Пример пятиугольной формы
Лица	3n треугольники п квадраты 1 н-угольник 1 2n-угольник
Края	9n
Вершины	5н
Группа симметрии	CNV, [n], (* nn)
Группа вращения	Cп, [n]+, (nn)
Двойной многогранник
Характеристики	выпуклый

В геометрия, то гиродлинные купола - бесконечное множество многогранников, построенных путем присоединения n-угольного купол к 2-угольному антипризма.

Есть три гиродлинные купола которые Твердые тела Джонсона сделаны из правильных треугольников и квадрата, и пятиугольника. Более высокие формы можно построить из равнобедренных треугольников. Примыкающий к треугольная призма к квадратная антипризма также образует многогранник, но имеет смежные параллельные грани, поэтому не является телом Джонсона. Шестиугольная форма может быть построена из правильных многоугольников, но все грани купола находятся в одной плоскости. Топологически другие формы можно построить без правильных граней.

Формы

	имя	лица
	гиродлинная треугольная призма	2 + 8 треугольников, 2 + 1 квадрат
	гировидный треугольный купол (J22)	9 + 1 треугольников, 3 квадрата, 1 шестиугольник
	гировидный квадратный купол (J23)	12 треугольников, 4 + 1 квадратов, 1 восьмиугольник
	гиродлинная пятиугольная куполка (J24)	15 треугольников, 5 квадратов, 1 пятиугольник, 1 десятиугольник
	гировидный шестиугольный купол	18 треугольников, 6 квадратов, 1 шестиугольник, 1 двенадцатиугольник

Смотрите также

• Вытянутый купол
• Удлиненная двуполость

Рекомендации

• Норман В. Джонсон, «Выпуклые тела с правильными гранями», Канадский математический журнал, 18, 1966, стр. 169–200. Содержит исходное перечисление 92 твердых тел и гипотезу о том, что других нет.
• Виктор Александрович Залгаллер (1969). Выпуклые многогранники с правильными гранями. Бюро консультантов. Нет ISBN. Первое доказательство того, что тел Джонсона всего 92.

Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. v т е