WikiDer > Удлиненная двуполость
| Набор удлиненных двупольных | |
|---|---|
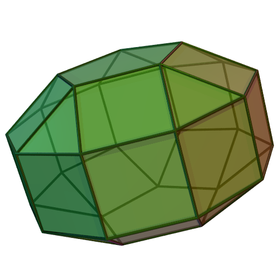 Пример пятиугольной орто-формы | |
| Лица | 2n треугольники 4n квадраты 2 н-угольник |
| Края | 12п |
| Вершины | 6п |
| Группа симметрии | Орто: Dпчас, [2, n], (* n22), порядок 4п Гироскоп: Dпd, [2+, 2n], (2 * n), порядок 4п |
| Свойства | выпуклый |
В геометрия, то удлиненные двуполые два бесконечных набора многогранники, построенный соединением двух п-гональный купола чтобы п-гональный призма. У них 2п треугольники, 4п квадраты, и 2 п-гон. Ортоформы имеют выровненный купол, в то время как гироскопические формы выровнены встречно.
| 3 | 4 | 5 |
|---|---|---|
| Ортобикупола удлиненная | ||
| J35 | Полурегулярный | J38 |
| Ортобикупола удлиненно-треугольной формы | Ортобикупола удлиненная квадратная (ромбокубооктаэдр) | Ортобикупола удлиненная пятиугольная |
 |  |  |
 |  |  |
| Гиробикупола удлиненная | ||
| J36 | J37 | J39 |
| Гиробикупола удлиненной треугольной формы | Гиробикупола удлиненная квадратная (псевдоромбокубооктаэдр) | Гиробикупола удлиненная пятиугольная |
 |  |  |
 |  |  |
Смотрите также
использованная литература
- Норман В. Джонсон, «Выпуклые тела с правильными гранями», Канадский математический журнал, 18, 1966, стр. 169–200. Содержит исходное перечисление 92 твердых тел и гипотезу о том, что других нет.
- Виктор Александрович Залгаллер (1969). Выпуклые многогранники с правильными гранями. Бюро консультантов. Нет ISBN. Первое доказательство того, что тел Джонсона всего 92.
| Эта многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |