WikiDer > Усеченный ромбокубооктаэдр
| Усеченный ромбокубооктаэдр | |
|---|---|
 | |
| Символ Шлефли | trr {4,3} = |
| Обозначение Конвея | TaaC |
| Лица | 50: 24 {4} 8 {6} 6+12 {8} |
| Края | 144 |
| Вершины | 96 |
| Группа симметрии | Очас, [4,3], (* 432) порядок 48 |
| Группа вращения | О, [4,3]+, (432), заказ 24 |
| Двойной многогранник | Disdyakis icositetrahedron |
| Свойства | выпуклый, зоноэдр |
В усеченный ромбокубооктаэдр это многогранник, построенный как усечение из ромбокубооктаэдр. У него 50 граней, состоящих из 18 восьмиугольников, 8 шестиугольников и 24 квадратов. Он может заполнить пространство усеченный куб, усеченный тетраэдр и треугольная призма как усеченный рунические кубические соты.
Другие имена
- Усеченный малый ромбокубооктаэдр
- Скошенный кубооктаэдр
Зоноэдр
Как зоноэдр, он может быть построен со всеми восьмиугольниками, кроме 12, как правильные многоугольники. Он имеет два набора из 48 вершин, находящихся на двух расстояниях от его центра.
Он представляет собой Сумма Минковского из куб, а усеченный октаэдр, а ромбический додекаэдр.
Раскопанный усеченный ромбокубооктаэдр
| Раскопанный усеченный ромбокубооктаэдр | |
|---|---|
| Лица | 148: 8 {3} 24+96+6 {4} 8 {6} 6 {8} |
| Края | 312 |
| Вершины | 144 |
| Эйлерова характеристика | -20 |
| Род | 11 |
| Группа симметрии | Очас, [4,3], (* 432) порядок 48 |
Выкопанный усеченный ромбокубооктаэдр представляет собой тороидальный многогранник, построенный из усеченного ромбокубооктаэдра с удаленными 12 неправильными восьмиугольными гранями. Он включает сеть из 6 квадратные купола, 8 треугольные купола, и 24 треугольные призмы. [1] У него 148 граней (8 треугольников, 126 квадратов, 8 шестиугольников и 6 восьмиугольников), 312 ребер и 144 вершины. С участием Эйлерова характеристика χ = f + v - e = -20, его род (g = (2-χ) / 2) равно 11.
Без треугольных призм тороидальный многогранник становится усеченным кубооктаэдром.
 | 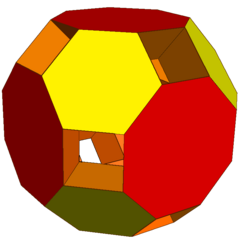 |
| Усеченный ромбокубооктаэдр | Усеченный кубооктаэдр |
|---|
Связанные многогранники
В усеченный кубооктаэдр аналогично, со всеми правильными гранями, и 4.6.8 вершина фигуры.
Треугольник и квадраты ромбокубооктаэдра могут быть независимо исправлены или усечены, создавая четыре перестановки многогранников. Частично усеченные формы можно рассматривать как краевые сокращения усеченной формы.
В усеченный ромбокубооктаэдр можно увидеть в последовательности исправление и усечение операции из кубооктаэдр. Дальше чередование шаг ведет к пренебрежительно ромбокубооктаэдр.
| имя | г {4,3} | рр {4,3} | tr {4,3} | Исправленный ррр {4,3} | Частично усечено | Усеченный trr {4,3} | srCO | |
|---|---|---|---|---|---|---|---|---|
| Конвей | AC | aaC = eC | taC = bC | aaaC = eaC | dXC | dXdC | taaC = baC | САК |
| Образ |  |  |  |  |  |  |  |  |
| VertFigs | 3.4.3.4 | 3.4.4.4 | 4.6.8 | 4.4.4.4d и 3.4.4d.4 | 4.4.4.6я и 4.6.6я | 4.6я.8 и 3.4.6я.4 | 4.8.8п и 4.6.8п | 3.3.3.3.4 и 3.3.4.3.4 |
Смотрите также
использованная литература
- Эппштейн, Дэвид (1996). «Зоноэдры и зонотопы». Математика в образовании и исследованиях. 5 (4): 15–21.
- Coxeter Правильные многогранники, Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (стр. 145–154 Глава 8: Усечение)
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5
внешние ссылки
- Переводчик Джорджа Харта Конвея: порождает многогранники в VRML, принимая нотацию Конвея в качестве входных данных
- Расширения призмы [1] Модель тороида
