WikiDer > Аполлонийская прокладка
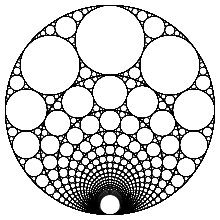
В математика, Аполлонийская прокладка или Аполлоническая сеть это фрактал генерируется, начиная с тройки кругов, каждая из которых касается двух других, и последовательно заполняет больше кругов, каждый касательная еще трем. Он назван в честь Греческий математик Аполлоний Пергский.[1]
строительство
Аполлоновскую прокладку можно построить следующим образом. Начните с трех кругов C1, C2 и C3, каждая из которых касается двух других (в общей конструкции эти три окружности должны быть разного размера и иметь общую касательную). Аполлоний обнаружил, что есть еще две непересекающиеся окружности: C4 и C5, которые имеют свойство касаться всех трех исходных окружностей - они называются Аполлонические круги. Добавив два аполлонических круга к исходным трем, мы получим пять кругов.
Возьмите один из двух аполлонических кругов - скажите C4. Это касается C1 и C2, поэтому тройка кругов C4, C1 и C2 имеет свои два аполлонических круга. Мы уже знаем один из них - это C3 - а другой - новый круг C6.
Аналогичным образом мы можем построить еще один новый круг C7 это касается C4, C2 и C3, и еще один круг C8 из C4, C3 и C1. Это дает нам 3 новых круга. Мы можем построить еще три новых круга из C5, всего шесть новых кругов. Вместе с кругами C1 к C5, это дает в общей сложности 11 кругов.
Продолжая таким образом строительство поэтапно, можно добавить 2 · 3п новые круги на сцене п, что в сумме дает 3п+1 + 2 круга после п этапы. В пределе этот набор кругов является прокладкой Аполлона.
Размеры новых кругов определяются Теорема Декарта. Позволять kя (за я = 1, ..., 4) обозначают искривления четырех взаимно касательных окружностей. Тогда теорема Декарта утверждает
(1)
Прокладка Аполлония имеет Хаусдорфово измерение около 1,3057.[2]
Кривизна
Кривизна окружности (изгиба) определяется как обратная ее радиусу.
- Отрицательная кривизна указывает на то, что все остальные круги касаются этой окружности изнутри. Это ограничивающий круг.
- Нулевая кривизна дает линию (круг с бесконечным радиусом).
- Положительная кривизна указывает на то, что все остальные круги касаются этой окружности снаружи. Этот круг находится внутри круга с отрицательной кривизной.
Вариации
Прокладку Аполлона также можно построить, заменив одну из образующих окружностей прямой линией, которую можно рассматривать как окружность, проходящую через бесконечно удаленную точку.
В качестве альтернативы, две образующие окружности могут быть заменены параллельными прямыми линиями, которые можно рассматривать как касательные друг к другу на бесконечности. В этой конструкции дополнительные круги образуют семейство Круги Форда.
Трехмерный эквивалент аполлоновской прокладки - это Упаковка аполлонических сфер.
Симметрии
Если две из исходных образующих окружностей имеют одинаковый радиус, а третья окружность имеет радиус, составляющий две трети этого, то аполлоновская прокладка имеет две линии отражающей симметрии; одна линия - линия, соединяющая центры одинаковых окружностей; другая - их касательная, проходящая через центр третьего круга. Эти линии перпендикулярны друг другу, поэтому аполлоновская прокладка также имеет вращательную симметрию степени 2; группа симметрии этой прокладки D2.
Если все три исходных образующих окружности имеют одинаковый радиус, тогда прокладка Аполлона имеет три линии отражающей симметрии; эти прямые являются взаимными касательными каждой пары окружностей. Каждая взаимная касательная также проходит через центр третьего круга и общий центр первых двух аполлонических кругов. Эти линии симметрии расположены под углами в 60 градусов друг к другу, поэтому аполлоническая прокладка также имеет вращательную симметрию степени 3; группа симметрии этой прокладки D3.
Ссылки с гиперболической геометрией
Три образующих круга, а следовательно, и вся конструкция, определяются положением трех точек, в которых они касаются друг друга. Поскольку есть Преобразование Мёбиуса который отображает любые три заданные точки на плоскости в любые другие три точки, и поскольку преобразования Мёбиуса сохраняют окружности, то существует преобразование Мёбиуса, которое отображает любые две аполлоновские прокладки друг в друга.
Преобразования Мёбиуса также являются изометриями гиперболическая плоскость, поэтому в гиперболической геометрии все аполлоновские прокладки конгруэнтны. Таким образом, в некотором смысле существует только одна аполлоновская прокладка с точностью до (гиперболической) изометрии.
Прокладка Аполлона - это предельный набор группы преобразований Мёбиуса, известной как Клейнианская группа.[3]
Интегральные аполлонические окружности
Интегральная аполлоническая упаковка кругов, определяемая кругом искривления из (−1, 2, 2, 3)
Если любые четыре касательных друг к другу окружности в аполлонической прокладке имеют целочисленную кривизну, то все круги в прокладке будут иметь целочисленную кривизну.[4]Поскольку уравнение, связывающее кривизну в аполлоновской прокладке, целое или нет, имеет вид
отсюда следует, что можно перейти от одной четверки кривизны к другой, Виета прыгает, как и при поиске нового Число Маркова. Первые несколько из этих встроенных прокладок Аполлония перечислены в следующей таблице. В таблице указаны кривизны самых больших окружностей прокладки. Только первые три кривизны (из пяти, показанных в таблице) необходимы для полного описания каждой прокладки - все остальные кривизны могут быть получены из этих трех.
|
Симметрия интегральных аполлонических упаковок кругов
Нет симметрии
Если ни одна из изгибов не повторяется в пределах первых пяти, прокладка не содержит симметрии, которая представлена группой симметрии C1; прокладка, описываемая кривизной (-10, 18, 23, 27), является примером.
D1 симметрия
Когда два из пяти наибольших кругов прокладки имеют одинаковую кривизну, эта прокладка будет иметь D1 симметрия, которая соответствует отражению вдоль диаметра ограничивающей окружности, без вращательной симметрии.
D2 симметрия
Если в пределах первых пяти повторяются две разные кривизны, прокладка будет иметь D2 симметрия; такая симметрия состоит из двух отражений (перпендикулярных друг другу) по диаметрам ограничивающей окружности с двойной симметрией поворота 180 °. Прокладка, описываемая кривизной (-1, 2, 2, 3), является единственной аполлоновой прокладкой (с точностью до масштабного коэффициента), которая обладает D2 симметрия.
D3 симметрия
Целочисленных прокладок с D3 симметрия.
Если три круга с наименьшей положительной кривизной имеют одинаковую кривизну, прокладка будет иметь D3 симметрии, которая соответствует трем отражениям по диаметрам ограничивающей окружности (разнесенной на 120 °), а также тройной вращательной симметрии 120 °. В этом случае отношение кривизны ограничивающей окружности к трем внутренним окружностям равно 2.√3 - 3. Поскольку это соотношение нерационально, никакие интегральные аполлонические кольцевые упаковки не обладают этим D3 симметрия, хотя многие упаковки приближаются.
Почти-D3 симметрия
На рисунке слева изображена цельная аполлоническая прокладка, которая, кажется, имеет D3 симметрия. Тот же рисунок показан справа, с метками, указывающими кривизну внутренних кругов, показывая, что прокладка фактически имеет только D1 симметрия, общая для многих других интегральных аполлоновских прокладок.
В следующей таблице перечислены другие почти-D3 интегральные аполлонические прокладки. Последовательность обладает некоторыми интересными свойствами, и в таблице перечислены факторизация кривизны, а также множитель, необходимый для перехода от предыдущего набора к текущему. Абсолютные значения кривизны дисков "а" подчиняются отношение повторения а(п) = 4а(п − 1) − а(п − 2) (последовательность A001353 в OEIS), откуда следует, что множитель сходится к √3 + 2 ≈ 3.732050807.
| Кривизна | Факторы | Множитель | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| а | б | c | d | а | б | d | а | б | c | d | ||
| −1 | 2 | 2 | 3 | 1×1 | 1×2 | 1×3 | Нет данных | Нет данных | Нет данных | Нет данных | ||
| −4 | 8 | 9 | 9 | 2×2 | 2×4 | 3×3 | 4.000000000 | 4.000000000 | 4.500000000 | 3.000000000 | ||
| −15 | 32 | 32 | 33 | 3×5 | 4×8 | 3×11 | 3.750000000 | 4.000000000 | 3.555555556 | 3.666666667 | ||
| −56 | 120 | 121 | 121 | 8×7 | 8×15 | 11×11 | 3.733333333 | 3.750000000 | 3.781250000 | 3.666666667 | ||
| −209 | 450 | 450 | 451 | 11×19 | 15×30 | 11×41 | 3.732142857 | 3.750000000 | 3.719008264 | 3.727272727 | ||
| −780 | 1680 | 1681 | 1681 | 30×26 | 30×56 | 41×41 | 3.732057416 | 3.733333333 | 3.735555556 | 3.727272727 | ||
| −2911 | 6272 | 6272 | 6273 | 41×71 | 56×112 | 41×153 | 3.732051282 | 3.733333333 | 3.731112433 | 3.731707317 | ||
| −10864 | 23408 | 23409 | 23409 | 112×97 | 112×209 | 153×153 | 3.732050842 | 3.732142857 | 3.732302296 | 3.731707317 | ||
| −40545 | 87362 | 87362 | 87363 | 153×265 | 209×418 | 153×571 | 3.732050810 | 3.732142857 | 3.731983425 | 3.732026144 | ||
Последовательные искривления
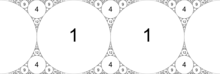
Для любого целого числа п > 0 существует аполлоновская прокладка, определяемая следующими кривизнами:
(−п, п + 1, п(п + 1), п(п + 1) + 1).
Например, прокладки, обозначенные (−2, 3, 6, 7), (−3, 4, 12, 13), (−8, 9, 72, 73) и (−9, 10, 90, 91 ) все следуют этому шаблону. Потому что каждый внутренний круг, определяемый п + 1 может стать ограничивающим кругом (определяемым -п) в другой прокладке эти прокладки могут быть вложенный. Это показано на рисунке справа, на котором изображены последовательные прокладки с п бег от 2 до 20.
Смотрите также
- Теорема Декарта, для кривизны взаимно касательных окружностей
- Форд круг, частный случай цельной аполлоновской прокладки (0,0,1,1)
- Серпинский треугольник
- Аполлоническая сеть, граф, полученный из конечных подмножеств аполлоновской прокладки
Примечания
- ^ Сатия, И. И., Бабочка в мире Иглесиаса Васиаса: история самого увлекательного квантового фрактала (Бристоль: IOP Publishing, 2016), п. 5.
- ^ Макмаллен, Кертис Т. (3 октября 1997 г.). "Размерность Хаусдорфа и конформная динамика III: Вычисление размерности", Abel.Math.Harvard.edu. Доступ: 27 октября 2018 г.
- ^ Счетные круги и эргодическая теория клейновых групп Хи О Брауна. Университет декабрь 2009 г.
- ^ Рональд Л. Грэм, Джеффри К. Лагариас, Колин М. Мэллоуз, Алан Р. Уилкс и Кэтрин Х. Ян; "Аполлонические упаковки кругов: теория чисел" J. Теория чисел, 100 (2003), 1-45
Рекомендации
- Бенуа Б. Мандельброт: Фрактальная геометрия природы, В. Х. Фриман, 1982, ISBN 0-7167-1186-9
- Пол Д. Бурк: "Введение в фрактал Аполлонии". Компьютеры и графика, том 30, выпуск 1, январь 2006 г., страницы 134–136.
- Дэвид Мамфорд, Кэролайн серии, Дэвид Райт: Жемчуг Индры: видение Феликса Кляйна, Издательство Кембриджского университета, 2002 г., ISBN 0-521-35253-3
- Джеффри К. Лагариас, Колин Л. Мэллоуз, Аллан Р. Уилкс: За пределами теоремы Декарта о круге, The American Mathematical Monthly, Vol. 109, No. 4 (апрель 2002 г.), стр. 338–361, (arXiv: math.MG/0101066 v1 9 января 2001 г.)
внешняя ссылка
| Викибук Фракталы есть страница по теме: Аполлонические фракталы |
- Вайсштейн, Эрик В. "Аполлонийская прокладка". MathWorld.
- Александр Богомольный, Аполлонийская прокладка, завязать узел
- Интерактивная аполлоническая прокладка, работающая на чистом HTML5 (ссылка мертвая)
- (по-английски) Скрипт Matlab для построения 2D аполлонической прокладки с n идентичными кругами с помощью инверсия круга
- Онлайн-эксперименты с JSXGraph
- Аполлонийская прокладка Майкл Скрайбер, Демонстрационный проект Wolfram.
- Интерактивная аполлонийская прокладка Демонстрация аполлонической прокладки на Java
- Дана Маккензи. Тискет, шкатулка, аполлонийская прокладка. Американский ученый, январь / февраль 2010 г.
- «Рисунок песком - крупнейшее в мире произведение искусства», Телеграф, 16 дек 2009 г.. Газетный рассказ о произведении искусства в виде частичной аполлонической прокладки с внешней окружностью в девять миль.
- (на итальянском)Динамические аполлонические прокладки , Тартапелаг Джорджо Пьетрокола, 2014.