WikiDer > О размерах и расстояниях
О размерах и расстояниях (Солнца и Луны) (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri Megethon Kai апостематон) - текст древнего Греческий астроном Гиппарх (c. 190 - c. 120 г. до н.э.), в котором делаются аппроксимации радиусов солнце и Луна а также их расстояния от земной шар. Это не так сохранившийся, но часть его содержания сохранилась в произведениях Птолемей и его комментатор Папп Александрийский. Некоторые современные историки пытались реконструировать методы Гиппарха, используя доступные тексты.
Источники
Большая часть того, что известно о тексте Гиппарха, происходит из двух древних источников: Птолемея и Паппа. Работа также упоминается Теон Смирнский и другие, но их рассказы оказались менее полезными при реконструкции процедур Гиппарха.
Птолемей
В Альмагест V, 11, Птолемей пишет:
- Теперь Гиппарх проводил такое исследование в основном с помощью солнца. Поскольку из других свойств Солнца и Луны (изучение которых будет проведено ниже) следует, что если дано расстояние одного из двух светил, то расстояние до другого также задано, он пытается, предполагая расстояние солнце, чтобы продемонстрировать расстояние до Луны. Во-первых, он предполагает, что солнце демонстрирует наименее заметный параллакс, чтобы определить расстояние до него. После этого он использует приведенное им солнечное затмение, сначала как будто солнце не показывает заметного параллакса, и именно по этой причине отношения расстояний до Луны казались ему разными для каждой из выдвинутых им гипотез. Но что касается Солнца, то не только величина его параллакса, но и то, показывает ли оно вообще какой-либо параллакс, вообще сомнительно.
Этот отрывок дает общее описание того, что сделал Гиппарх, но не содержит подробностей. Птолемей явно не соглашался с методами, использованными Гиппархом, и поэтому не вдавался в подробности.
Папп Александрийский
Работы Гиппарха еще существовали, когда Папп написал свой комментарий к Альмагест в 4 веке. Он дополняет некоторые детали, которые опускает Птолемей:
- Гиппарх проводил такое исследование в основном с помощью солнца, и это было неточно. Поскольку, поскольку Луна в сизигиях и на ближайшем к ней наибольшем расстоянии кажется равной Солнцу, и поскольку дан размер диаметров Солнца и Луны (о чем будет сказано ниже), то из этого следует, что если расстояние в один между двумя светилами дано расстояние до другого, как в теореме 12, если дано расстояние до Луны и диаметры Солнца и Луны, то дано расстояние до Солнца. Гиппарх пытается, предполагая параллакс и расстояние до Солнца, продемонстрировать расстояние до Луны, но относительно Солнца не только величина его параллакса, но и то, показывает ли он вообще какой-либо параллакс, вообще сомнительно. Таким образом, Гиппарх сомневался в солнце, не только в величине его параллакса, но и в том, показывает ли оно вообще какой-либо параллакс. В первой книге «О размерах и расстояниях» предполагается, что Земля имеет соотношение точки и центра к Солнцу. И с помощью приведенного им затмения ...
Тогда позже,
- Ибо в книге 1 «О размерах и расстояниях» он делает следующее наблюдение: солнечное затмение, которое в регионах вокруг Геллеспонта было точным затмением всего солнечного диска, так что никакая его часть не была видна, но в Александрии Египтом было затмено примерно четыре пятых ее площади. Посредством этого он показывает в Книге 1, что в единицах, из которых радиус Земли равен единице, наименьшее расстояние до Луны составляет 71, а наибольшее - 83. Следовательно, среднее значение равно 77 ... Затем снова он сам в Книга 2 "О размерах и расстояниях" показывает из многих соображений, что в единицах, в которых радиус Земли равен единице, наименьшее расстояние до Луны равно 62, а среднее - 67.1⁄3, а расстояние до Солнца 490. Ясно, что наибольшее расстояние до Луны составляет 722⁄3.
Этот отрывок предоставляет достаточно деталей, чтобы сделать реконструкцию возможной. В частности, разъясняется, что было две отдельные процедуры, и даются точные результаты каждой. Он дает ключи, с помощью которых можно идентифицировать затмение, и говорит, что Гиппарх использовал формулу «как в теореме 12», теореме Птолемея, которая дошла до нас.
Современные реконструкции
Некоторые историки науки пытались реконструировать расчеты, использованные в О размерах и расстояниях. Первую попытку предпринял Фридрих Гульч в 1900 году, но позже он был отвергнут Ноэль Свердлоу в 1969 г. Дж. Дж. Тумер расширил свои усилия в 1974 году.
Hultsch
Фридрих Хульш в статье 1900 года определил, что источник Паппа был неправильно скопирован и что фактическое расстояние до Солнца, рассчитанное Гиппархом, составляло 2490 земных радиусов (а не 490). Как и в английском, между этими двумя результатами в греческом языке разница только в один символ.
Его анализ был основан на тексте Теон Смирнский в котором говорится, что Гиппарх обнаружил, что Солнце в 1880 раз больше Земли, а Земля в 27 раз больше Луны. Предполагая, что это относится к объемам, следует, что
и
Предполагая, что Солнце и Луна имеют одинаковый видимый размер на небе, а Луна - 671⁄3 Земные радиусы далеки, отсюда следует, что
Этот результат был общепринятым в течение следующих семидесяти лет, пока Ноэль Свердлоу повторно расследовал дело.
Книга 2 реконструкция (Свердлов)
Свердлоу определил, что Гиппарх связывает расстояния до Солнца и Луны, используя конструкцию, найденную в Птолемей. Было бы неудивительно, если бы этот расчет был первоначально разработан самим Гиппархом, поскольку он был основным источником для Альмагест.
Используя этот расчет, Свердлов смог связать два результата Гиппарха (671⁄3 для Луны и 490 для Солнца). Для точного получения этого соотношения необходимо следовать очень точному набору приближений.
Использование простых тригонометрических тождеств дает
и
По параллельным линиям и взявт = 1, получаем
По подобию треугольников
Объединение этих уравнений дает
Значения, которые Гиппарх принял для этих переменных, можно найти в книге Птолемея. Альмагест IV, 9. Он говорит, что Гиппарх обнаружил, что Луна измерила свой собственный круг примерно 650 раз, и что угловой диаметр тени Земли в 2,5 раза больше диаметра Луны. Папп сообщает нам, что Гиппарх считал среднее расстояние до Луны равным 671⁄3. Это дает:
| Количество | Ценить |
|---|---|
| 671⁄3 |
Согласно Свердлову, Гиппарх теперь оценил это выражение с помощью следующих округлений (значения указаны в шестидесятеричный):
и
Тогда, потому что
следует, что
Свердлоу использовал этот результат, чтобы доказать, что 490 было правильным прочтением текста Паппа, тем самым опровергая интерпретацию Хульша. Хотя этот результат сильно зависит от конкретных используемых приближений и округлений, он был общепринятым. Однако остается открытым вопрос о том, где расстояние до Луны 671⁄3 пришли из.
Вслед за Паппом и Птолемеем Свердлов предположил, что Гиппарх оценил 490 радиусов Земли как минимально возможное расстояние до Солнца. Это расстояние соответствует солнечному параллаксу 7 ', который, возможно, был максимумом, который, по его мнению, остался бы незамеченным (типичное разрешение человеческого глаза - 2'). Полученную выше формулу для расстояния до Солнца можно инвертировать, чтобы определить расстояние до Луны:
Используя те же значения, что и выше для каждого угла, и используя 490 земных радиусов в качестве минимального солнечного расстояния, следует, что максимальное среднее расстояние до Луны составляет
Тумер расширил этот вопрос, заметив, что по мере неограниченного увеличения расстояния до Солнца формула приближается к минимальному среднему лунному расстоянию:
Это близко к значению, которое позже утверждал Птолемей.
Реконструкция книги 1 (Toomer)
В дополнение к объяснению минимального лунного расстояния, которого достиг Гиппарх, Тумер смог объяснить метод первой книги, в которой использовался солнечное затмение. Папп утверждает, что это затмение было полным в районе Геллеспонта, но наблюдалось как 4/5 от общего числа в Александрии.
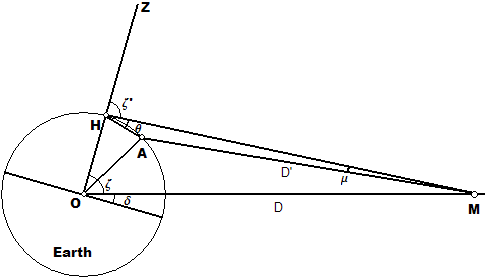
Если Гиппарх предположил, что Солнце бесконечно удалено (т.е. что «Земля имеет отношение точки и центра к Солнцу»), то разница в величине солнечного затмения должна быть полностью обусловлена параллаксом Луны. Используя данные наблюдений, он сможет определить этот параллакс и, следовательно, расстояние до Луны.
Гиппарх знал бы и , то широты из Александрия и Геллеспонтинский регион, соответственно. Он также знал бы , то склонение Луны во время затмения, и , что связано с разницей в полноте затмения между двумя регионами.
Crd здесь относится к аккорд функция. Поскольку Луна очень далеко, отсюда следует, что . Использование этого приближения дает
Следовательно,
С и , нам нужно только получить . Поскольку затмение было полным в H и 4/5 в A, отсюда следует, что составляет 1/5 видимого диаметра Солнца. Это количество было хорошо известно Гиппарху - он полагал, что оно составляет 1/650 полного круга. Тогда расстояние от центра Земли до Луны следует из .
Тумер определил, как Гиппарх определил хорду для малых углов (см. Хорда (геометрия)). Его значения для широты Геллеспонта (41 градус) и Александрии (31 градус) известны из Страбона работа над География. Чтобы определить склонение, необходимо знать, какое затмение использовал Гиппарх.
Поскольку он знал значение, которое Гиппарх в конечном итоге дал расстоянию до Луны (71 радиус Земли) и грубой области затмения, Тумер смог определить, что Гиппарх использовал затмение 14 марта 190 г. до н. Э. Это затмение очень хорошо соответствует всем математическим параметрам, а также имеет смысл с исторической точки зрения. Затмение было полным в Никее, Место рождения Гиппарха, так что он, возможно, слышал о нем. Об этом также говорится в Страбона Ab Urbe Condita VIII.2. Склонение Луны в это время было . Следовательно, используя тригонометрию хорд, дает
Теперь, используя таблицы аккордов Гиппарха,
и поэтому
Это хорошо согласуется со значением 71 радиуса Земли, которое сообщает Папп.
Этот анализ предполагал, что затмение произошло в середине дня, когда Солнце и Луна находились на меридиане. Но этого не произошло с затмением 190 г. до н.э., которое произошло ранним утром 28 февраля. [1]
Вывод
Если предположить, что эти реконструкции точно отражают то, что писал Гиппарх в О размерах и расстояниях, тогда эта работа была замечательным достижением. Такой подход к установлению ограничений на неизвестную физическую величину не был новым для Гиппарха (см. Аристарх Самосский. Архимед сделал то же самое с число Пи), но в тех случаях границы отражали неспособность определить математическую константу с произвольной точностью, а не неопределенность в физических наблюдениях.
Гиппарх, похоже, в конце концов разрешил противоречие между двумя своими результатами. Его целью при вычислении расстояния до Луны было получение точного значения лунного параллакса, чтобы он мог предсказывать затмения с большей точностью. Для этого он должен был выбрать конкретное значение расстояния / параллакса, а не диапазон значений.
Есть некоторые свидетельства того, что он это сделал. Комбинируя расчеты Книги 2 и учет Теон Смирнский дает расстояние до Луны 60,5 радиуса Земли. То же самое и с учётом Клеомед дает расстояние 61 земной радиус. Они удивительно близки как к оценке Птолемея, так и к современной.
По словам Тумера,
- Эта процедура, если я построил ее правильно, очень замечательна ... Удивительна изощренность подхода к проблеме двумя совершенно разными методами, а также полная честность, с которой Гиппарх раскрывает свои противоречивые результаты ... которые, тем не менее, являются такого же порядка величины и (впервые в истории астрономии) в правой области.
Смотрите также
- Аристарх Самосский, греческий математик, вычисливший расстояние от Земли до Солнца.
- Эратосфен, греческий математик, вычисливший расстояние от Земли до Солнца.
- Греческая математика
- Гиппарх
- Посидоний, греческий философ, вычисливший длину окружности Земли.
Рекомендации
- ^ https://eclipse.gsfc.nasa.gov/JLEX/JLEX-AS.html NASA Javascript Lunar Eclipse Explorer около Александрии (40 ° 25 ′ 45 ″ северной широты, 29 ° 43 ′ 16 ″ восточной долготы) в -189 г. до н.э.
- Ф. Хульч, "...," Лейпциг, Phil.-hist. Kl. 52 (1900), 169–200.
- Н. М. Свердлов, «Гиппарх на расстоянии солнца», Центавр 14 (1969), 287–305.
- Дж. Дж. Тумер, "Гиппарх на расстояниях солнца и луны", Архив истории точных наук. 14 (1974), 126–142.
- Хон, Гиора. «Есть ли в греческой астрономии понятие экспериментальной ошибки?» Британский журнал истории науки 22.02 (1989): 129-150. (Доступно на сайте https://www.researchgate.net/profile/Giora_Hon/publication/231844424_Is_There_a_Concept_of_Experimental_Error_in_Greek_Astronomy/links/564fa57b08ae4988a7a858bd.pdf)
![s = sqrt [3] {1880} приблизительно 12 + 1/3](https://wikimedia.org/api/rest_v1/media/math/render/svg/6678c111258e1fe54fab52af3a309903da75b5aa)
![ell = sqrt [3] {1/27} = 1/3](https://wikimedia.org/api/rest_v1/media/math/render/svg/f05b15e9ac7e4e2f097031e721d3b2f57bf551b8)