WikiDer > Феодор из Кирены
Теодор из Кирена (Греческий: Θεόδωρος ὁ Κυρηναῖος) был древним ливийским греком и жил в 5 веке до нашей эры. Единственные выжившие свидетельства о нем из первых рук находятся в трех Платондиалоги: Theaetetus, то Софист, а Государственный деятель. В предыдущем диалоге он утверждает математическую теорему, теперь известную как Спираль Теодора.
Жизнь
О биографии Теодора известно немногое, кроме того, что можно вывести из диалогов Платона. Он родился в северной африканской колонии Кирена и, по-видимому, преподавал и там, и в Афинах.[1] Он жалуется на старость в Theaetetus, драматическая дата 399 г. до н.э. предполагает, что период его расцвета пришелся на середину V века. Текст также связывает его с софист Протагор, с которым он, по его словам, учился, прежде чем обратиться к геометрии.[2] Сомнительная традиция, повторяемая древними биографами, такими как Диоген Лаэртиус[3] считал, что Платон позже учился с ним в Кирена, Ливия.[1]
Работа по математике
Работа Теодора известна благодаря единственной теореме, изложенной в литературном контексте Theaetetus и утверждалось, что он был исторически точным или вымышленным.[1] В тексте его ученица Theaetetus приписывает ему теорему о том, что квадратные корни из неквадратных чисел до 17 иррациональны:
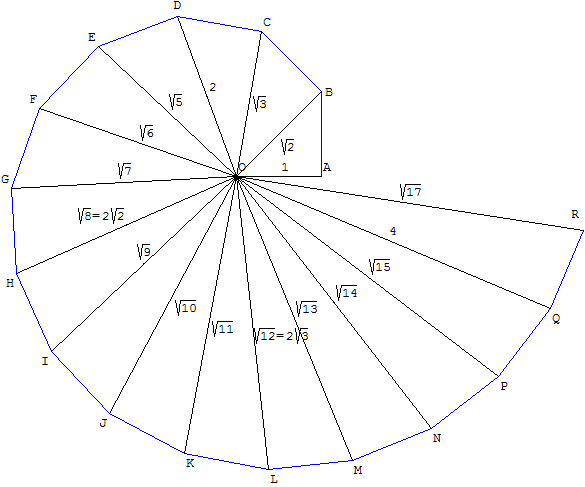
Теодор здесь рисовал для нас несколько фигур для иллюстрации корней, показывая, что квадраты, содержащие три квадратных фута и пять квадратных футов, не соизмеримы по длине с единицей фута, и поэтому, выбирая каждый из них по очереди, до квадрата, содержащего семнадцать квадратных футов, и на этом он остановился.[4]
(Квадрат, содержащий два квадратных единиц не упоминается, возможно, потому, что несоизмеримость его стороны с единицей уже была известна.) Метод доказательства Теодора неизвестен. Неизвестно даже, означает ли в процитированном отрывке «до» (μέχρι) семнадцать. Если семнадцать исключено, то доказательство Теодора могло полагаться только на рассмотрение того, являются ли числа четными или нечетными. Действительно, Харди и Райт[5]и Кнорр[6] предложить доказательства, которые в конечном итоге опираются на следующую теорему: если растворяется в целых числах, а странно, то должно быть конгруэнтный к 1 по модулю 8 (поскольку и можно считать нечетными, поэтому их квадраты сравнимы с 1 по модулю 8).
Возможность, предложенная ранее Zeuthen[7] заключается в том, что Теодор применил так называемое Евклидов алгоритм, сформулированные в предложении X.2 Элементы как тест на несоизмеримость. Говоря современным языком, теорема состоит в том, что действительное число с бесконечный непрерывная дробь расширение иррационально. Иррациональные квадратные корни имеют периодические расширения. Период квадратного корня из 19 имеет длину 6, что больше периода квадратного корня из любого меньшего числа. Период √17 имеет длину единицу (как и √18; но иррациональность √18 следует из что из √2).
Так называемая Спираль Теодора состоит из смежных прямоугольные треугольники с участием гипотенуза длины равны √2, √3, √4,…, √17; дополнительные треугольники приводят к наложению диаграммы. Филип Дж. Дэвис интерполированный вершины спирали, чтобы получилась непрерывная кривая. В своей книге он обсуждает историю попыток определить метод Теодора. Спирали: от Теодора к хаосу, и делает краткие ссылки на этот вопрос в своей художественной Томас Грей серии.
То, что Теэтет установил более общую теорию иррациональных чисел, согласно которой квадратные корни из неквадратных чисел являются иррациональными, предполагается в одноименном платоническом диалоге, а также в комментариях к нему. схолия к, Элементы.[8]
Смотрите также
- Хронология древнегреческих математиков
- Список выступающих в диалогах Платона
- Квадратичный иррациональный
- Уилбур Норр
использованная литература
- ^ а б c Гвозди, Дебра (2002). Люди Платона: Просопография Платона и других сократиков. Индианаполис: Хакетт. стр.281-2.
- ^ c.f. Платон, Theaetetus, 189а
- ^ Диоген Лаэртийский 3.6
- ^ Платон. Кратил, Теэтет, Софист, Государственный деятель. п. 174d. Получено 5 августа, 2010.
- ^ Харди, Г. Х.; Райт, Э.М. (1979). Введение в теорию чисел. Оксфорд. стр.42–44. ISBN 0-19-853171-0.
- ^ Кнорр, Уилбур (1975). Эволюция евклидовых элементов. Д. Рейдел. ISBN 90-277-0509-7.
- ^ Хит, Томас (1981). История греческой математики. Vol. 1. Дувр. п. 206. ISBN 0-486-24073-8.CS1 maint: ref = harv (ссылка на сайт)
- ^ Хит 1981, п. 209.
дальнейшее чтение
- Чойк, Джеймс Р. (1980). «Доказательства иррациональности Теодора». Двухлетний математический журнал колледжа.
- Гоу, Джеймс (1884). Краткая история греческой математики. Университетская пресса. п.85.