WikiDer > Изотоксический показатель
В геометрия, а многогранник (например, многоугольник или многогранник) или черепица, является изотоксальный или же реберно-транзитивный если это симметрии действовать переходно по его краям. Неформально это означает, что у объекта есть только один тип ребра: при наличии двух ребер происходит перемещение, вращение и / или отражение, которые перемещают один край к другому, оставляя область, занятую объектом, неизменной.
Период, термин изотоксальный происходит от греческого τοξον, что означает дуга.
Изотоксические полигоны
Изотоксальный многоугольник - это равносторонний многоугольник, но не все равносторонние многоугольники изотоксальны. В двойники изотоксальных полигонов изогональные многоугольники.
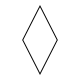
В общем, изотоксал 2п-гон будет иметь Dп (*nn) двугранная симметрия. А ромб - изотоксальный многоугольник с D2 (* 22) симметрия.
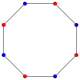
Все правильные многоугольники (равносторонний треугольник, квадрати др.) изотоксичны, имеют двойной минимальный порядок симметрии: регулярный п-gon имеет Dп (*nn) двугранная симметрия. Обычный 2п-gon является изотоксическим многоугольником и может быть помечен чередующимися цветными вершинами, удаляя линию отражения через средние края.
| D2 (*22) | D3 (*33) | D4 (*44) | D5 (*55) | |||||
|---|---|---|---|---|---|---|---|---|
| Ромб | Равносторонний треугольник | Вогнутый шестиугольник | Самопересекающийся шестиугольник | Выпуклый восьмиугольник | Обычный пятиугольник | Самопересекающиеся (регулярные) пентаграмма | Самопересекающийся декаграмма | |
 |  |  |  |  |  |  |  |  |
Изотоксальные многогранники и мозаики
Правильные многогранники являются изоэдральными (гранно-транзитивными), изогональными (вершинно-транзитивными) и изотоксальными (реберно-транзитивными).
Квазирегулярный многогранники, как и кубооктаэдр и икосододекаэдр, являются изогональными и изотоксальными, но не изоэдральными. Их двойники, включая ромбический додекаэдр и ромбический триаконтаэдр, являются изоэдральными и изотоксальными, но не изогональными.
| Квазирегулярный многогранник | Квазирегулярный дуальный многогранник | Квазирегулярный звездный многогранник | Квазирегулярный дуальный звездный многогранник | Квазирегулярный черепица | Квазирегулярный дуальный черепица |
|---|---|---|---|---|---|
 А кубооктаэдр является изогональным и изотоксальным многогранником |  А ромбический додекаэдр является изоэдральным и изотоксальным многогранником |  А большой икосододекаэдр является изогональным и изотоксальным звездчатым многогранником |  А большой ромбический триаконтаэдр - изоэдрический и изотоксальный звездный многогранник |  В трехгексагональная черепица является изогональным и изотоксальным замощением |  В ромбовидная плитка - изоэдрическая и изотоксическая мозаика с симметрией p6m (* 632). |
Не каждый многогранник или 2-х мерный мозаика построен из правильные многоугольники изотоксален. Например, усеченный икосаэдр (знакомый футбольный мяч) не изотоксален, так как у него два типа ребер: шестиугольник-шестиугольник и шестиугольник-пятиугольник, и симметрия твердого тела не может переместить грань шестиугольника-шестиугольника на грань шестиугольника-пятиугольника.
Изотоксальный многогранник имеет то же двугранный угол для всех краев.
Двойник выпуклого многогранника также является выпуклым многогранником.[1]
Двойник невыпуклого многогранника также является невыпуклым многогранником.[1] (По контрасту.)
Двойник изотоксального многогранника также является изотоксальным многогранником. (См. Двойной многогранник статья.)
Есть девять выпуклый изотоксальные многогранники: пятерка (обычный) Платоновы тела, два (квазирегулярный) общие ядра двойственных Платоновых тел и их два двойственных.
Всего четырнадцать невыпуклых изотоксальных многогранников: четыре (правильных) Многогранники Кеплера – Пуансо, два (квазирегулярных) общих ядра двойственных многогранников Кеплера – Пуансо и их два двойных, плюс три квазирегулярных дитригональных (3 | п q) звездные многогранники и три двойных к ним.
Существует по крайней мере пять изотоксальных полиэдрических соединений: пять правильные полиэдральные соединения; их пять двойников также являются пятью правильными полиэдрическими соединениями (или одним хиральным двойником).
Существует по крайней мере пять изотоксальных многоугольных мозаик евклидовой плоскости и бесконечно много изотоксальных многоугольных мозаик гиперболической плоскости, включая конструкции Витхоффа из регулярные гиперболические мозаики {п,q}, и неправильный (p q r) группы.
Смотрите также
Рекомендации
- ^ а б "двойственность". maths.ac-noumea.nc. Получено 2020-09-30.
- Питер Р. Кромвель, Многогранники, Издательство Кембриджского университета 1997, ISBN 0-521-55432-2, п. 371 Транзитивность
- Грюнбаум, Бранко; Шепард, Г. К. (1987). Плитки и узоры. Нью-Йорк: У. Х. Фриман. ISBN 0-7167-1193-1. (6.4 Изотоксальные плитки, 309-321)
- Коксетер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446, S2CID 202575183