WikiDer > Равносторонний многоугольник
Эта статья нужны дополнительные цитаты для проверка. (Август 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В геометрия, три или более трех прямых (или сегментов линии) образуют многоугольник и равносторонний многоугольник это многоугольник у которого все стороны одинаковой длины. За исключением треугольник случае, это не должно быть равносторонний (не обязательно, чтобы все углы были равны), но если это так, то это правильный многоугольник. Если количество сторон не менее пяти, равносторонний многоугольник не обязательно должен быть выпуклый многоугольник: возможно вогнутый или даже самопересекающийся.
Примеры
Все правильные многоугольники и изотоксальные многоугольники равносторонние.
An равносторонний треугольник это обычный треугольник с 60 ° внутренние углы.
Равносторонний четырехугольник называется ромб, изотоксальный многоугольник описывается углом α. Он включает квадрат как частный случай.
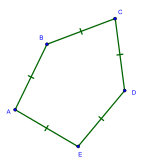
Выпуклый равносторонний пятиугольник можно описать двумя углами α и β, которые вместе определяют другие углы. Вогнутый равносторонний пятиугольники существуют, как и вогнутые равносторонние многоугольники с любым большим числом сторон.
Равносторонний многоугольник циклический (его вершины лежат на окружности) является правильный многоугольник (многоугольник, который является как равносторонним, так и равносторонний).
А касательный многоугольник (тот, у которого есть окружать касательная ко всем его сторонам) является равносторонним тогда и только тогда, когда чередующиеся углы равны (то есть, углы 1, 3, 5, ... равны, а углы 2, 4, ... равны). Таким образом, если количество сторон п нечетно, касательный многоугольник равносторонний тогда и только тогда, когда он правильный.[1]
Теорема Вивиани обобщается на равносторонние многоугольники:[2] Сумма расстояний по перпендикулярам от внутренней точки до сторон равностороннего многоугольника не зависит от расположения внутренней точки.
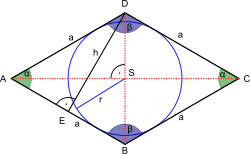
В главные диагонали из шестиугольник каждый делит шестиугольник на четырехугольники. В любом выпуклом равностороннем шестиугольнике с общей стороной а, Существует[3]:стр.184, № 286.3 главная диагональ d1 такой, что
и главная диагональ d2 такой, что
Триамби
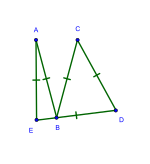
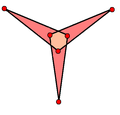
Триамби равносторонние шестиугольники с тригональной симметрией:
Рекомендации
- ^ Де Вильерс, Майкл (март 2011 г.), «Равноугольные циклические и равносторонние описанные многоугольники» (PDF), Математический вестник, 95: 102–107.
- ^ Де Вильерс, Майкл, «Иллюстрация объяснительной и открывающей функций доказательства», Леонардо, 33 (3): 1–8,
объяснение (доказательство) теоремы Вивиани для равностороннего треугольника путем определения площади трех треугольников, на которые он разделен, и замечая «общий множитель» равных сторон этих треугольников как оснований, может позволить сразу увидеть, что результат обобщается на любой равносторонний многоугольник
. - ^ Неравенства, предложенные в «Crux Mathematicorum”, [1].
внешняя ссылка
 СМИ, связанные с Равносторонние многоугольники в Wikimedia Commons
СМИ, связанные с Равносторонние многоугольники в Wikimedia Commons- Равносторонний треугольник С интерактивной анимацией
- Свойство равносторонних многоугольников: о чем оно? обсуждение теоремы Вивиани на Разрезать узел.