WikiDer > Enneacontagon

Обычный эннаконтагон
Обычный энниконтагон
Тип	Правильный многоугольник
Края и вершины	90
Символ Шлефли	{90}, т {45}
Диаграмма Кокстера
Группа симметрии	Двугранный (D90), заказ 2 × 90
Внутренний угол (градусы)	176°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, эннаконтагон или же enenecontagon или 90-угольник (от Древнегреческий ἑννενήκοντα, девяносто^[1]) является девяностаугольным многоугольник.^[2][3] Сумма внутренних углов любого эннаконтагона составляет 15840 градусов.

А обычный эннаконтагон представлен Символ Шлефли {90} и может быть выполнен в виде усеченный тетраконтапентагон, t {45}, который чередует два типа ребер.

Обычные свойства эннаконтагона

Один внутренний угол в обычном энеконтагоне равен 176 °, что означает, что один внешний угол будет равен 4 °.

В площадь регулярного эннаконтагона (с т = длина кромки)

${ displaystyle A = { frac {45} {2}} t ^ {2} cot { frac { pi} {90}}}$

и это inradius является

${ displaystyle r = { frac {1} {2}} t cot { frac { pi} {90}}}$

В по окружности регулярного эннаконтагона

${ displaystyle R = { frac {1} {2}} t csc { frac { pi} {90}}}$

Поскольку 90 = 2 × 3² × 5, обычный энниконтагон не конструктивный используя компас и линейка,^[4] но конструктивно, если использование тройной угол позволено.^[5]

Симметрия

Симметрии правильного эннаконтагона, разделенного на 6 подграфов, содержащих подгруппы индекса 2. Каждая симметрия внутри подграфа связана с нижними связными подграфами индексом 3 или 5.

В обычный энниконтагон есть Dih₉₀ двугранная симметрия, порядок 180, представленный 90 линиями отражения. Dih₉₀ имеет 11 диэдральных подгрупп: Dih₄₅, (Dih₃₀, Ди₁₅), (Dih₁₈, Ди₉), (Dih₁₀, Ди₅), (Dih₆, Ди₃) и (Dih₂, Ди₁). И еще 12 циклический симметрии: (Z₉₀, Z₄₅), (Z₃₀, Z₁₅), (Z₁₈, Z₉), (Z₁₀, Z₅), (Z₆, Z₃) и (Z₂, Z₁), причем Z_п представляющий π /п радианная вращательная симметрия.

Эти 24 симметрии связаны с 30 различными симметриями на эннаконтагоне. Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой.^[6] Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии. а1 этикетки не симметричны.

Эти более низкие симметрии допускают степени свободы в определении нерегулярных эннеконтагонов. Только g90 симметрия не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

90-угольник с 3960 ромбами

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[7]В частности, это верно для правильные многоугольники с равным числом сторон, в этом случае все параллелограммы ромбовидны. Для обычный энниконтагон, м= 45, его можно разделить на 990: 22 набора по 45 ромбов. Это разложение основано на Многоугольник Петри проекция 45-куб.

Примеры

Эннеаконтаграмма

Эннеаконтаграмма - это 90-гранная звездный многоугольник. Есть 11 обычных форм, которые дает Символы Шлефли {90/7}, {90/11}, {90/13}, {90/17}, {90/19}, {90/23}, {90/29}, {90/31}, {90 / 37}, {90/41} и {90/43}, а также 33 обычных звездные фигуры с тем же конфигурация вершины.

Обычный звездные многоугольники {90 / к}

Картинки	{90/7}	{90/11}	{90/13}	{90/17}	{90/19}	{90/23}
Внутренний угол	152°	136°	128°	112°	104°	88°
Картинки	{90/29}	{90/31}	{90/37}	{90/41}	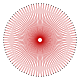{90/43}
Внутренний угол	64°	56°	32°	16°	8°

Рекомендации

• Вайсштейн, Эрик В. «Эннеконтагон». MathWorld.
• Именование многоугольников и многогранников
• эненаконтагон