WikiDer > Додекаграмма - Википедия
 | Эта статья нужны дополнительные цитаты для проверка. (Август 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Обычная додекаграмма | |
|---|---|
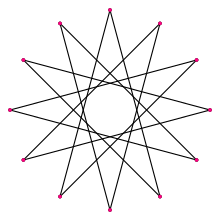 Обычная додекаграмма | |
| Тип | Правильный звездный многоугольник |
| Края и вершины | 12 |
| Символ Шлефли | {12/5} т {6/5} |
| Диаграмма Кокстера |       |
| Группа симметрии | Двугранный (D12) |
| Внутренний угол (градусы) | 30° |
| Двойной многоугольник | себя |
| Характеристики | звезда, циклический, равносторонний, изогональный, изотоксальный |
| Звездные многоугольники |
|---|
А додекаграмма это звездный многоугольник это 12 вершины. Есть одна обычная форма: {12/5}. Обычная додекаграмма имеет то же самое расположение вершин как обычный двенадцатигранник, что можно рассматривать как {12/1}.
Название «додекаграмма» объединяет цифровой префикс додека- с Греческий суффикс -грамма. В -грамма суффикс происходит от γραμμῆς (граммы), что обозначает линию.[1]
Изогональные вариации
Правильную додекаграмму можно рассматривать как квазиусеченный шестиугольник, t {6/5} = {12/5}. Другой изогональный (вершинно-транзитивный) варианты с одинаковыми вершинами могут быть построены с двумя длинами ребер.
 т {6} |  |  |  т {6/5} = {12/5} |
Додекаграммы как соединения
Есть четыре обычных додекаграммы звездные фигуры: {12/2} = 2 {6}, {12/3} = 3 {4}, {12/4} = 4 {3} и {12/6} = 6 {2}. Первый - это соединение двух шестиугольники, второй - соединение трех квадраты, третий - соединение четырех треугольники, а четвертый - соединение шести прямолинейных дигоны. Последние два можно считать соединением двух гексаграммы и последний как три тетраграммы.
.svg) 2{6} | .svg) 3{4} | .svg) 4{3} | .svg) 6{2} |
Полный график
Наложение всех додекагонов и додекаграмм друг на друга, включая выродиться соединение шести дигоны (отрезки), {12/6} - производит полный график K12.
 | черный: двенадцать угловых точек (узлов) красный: {12} правильный двенадцатигранник |
Правильные додекаграммы в многогранниках
Додекаграммы также могут быть включены в равномерные многогранники. Ниже приведены три призматические однородные многогранники содержащие правильные додекаграммы (других однородных многогранников, содержащих додекаграммы, не существует).
Додекаграммы также могут быть включены в звездные мозаики евклидовой плоскости.
Символизм Додекаграммы
Додекаграммы или двенадцатиконечные звезды использовались как символы для следующего:
- двенадцать колен Израилевых в иудаизме
- двенадцать учеников в христианстве
- двенадцать олимпийцев в греческом политеизме
- двенадцать знаков зодиака
- Международный Орден Двенадцати Рыцарей и Дочерей Фавора, афро-американская братская группа
- вымышленное тайное общество Мануса Санкти, в Рыцари Мануса Санкти серия Брин Донован
- Двенадцать племен Науру на государственном флаге.
Смотрите также
Рекомендации
- Вайсштейн, Эрик В. «Додекаграмма». MathWorld.
- Грюнбаум, Б. и G.C. Шепард; Плитки и узоры, Нью-Йорк: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B .; Многогранники с полыми гранями, Протокол конференции НАТО-АСИ по многогранникам ... и т. Д. (Торонто, 1993 г.), под ред. Т. Бистрички и др., Kluwer Academic (1994), стр. 43–70.
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. с. 404: Правильные звездные многогранники размерности 2)