WikiDer > Хендекаграмма

Hendecagram
Хендекаграмма
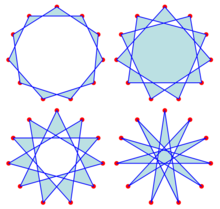HendecagramTypes.png
Четыре обычных хендекаграммы
Края и вершины11
Символ Шлефли{11/2}, {11/3}
{11/4}, {11/5}
Диаграмма КокстераCDel node 1.pngCDel 11.pngCDel rat.pngCDel d2.pngCDel node.png, CDel node 1.pngCDel 11.pngCDel rat.pngCDel d3.pngCDel node.png
CDel node 1.pngCDel 11.pngCDel rat.pngCDel d4.pngCDel node.png, CDel node 1.pngCDel 11.pngCDel rat.pngCDel d5.pngCDel node.png
Группа симметрииDih11, заказ 22
Внутренний угол (градусы)≈114.545° {11/2}
≈81.8182° {11/3}
≈49.0909° {11/4}
≈16.3636° {11/5}

В геометрия, а хендкаграмма (также эндекаграмма или же эндекаграмма) это звездный многоугольник это одиннадцать вершины.

Название хендкаграмма сочетает в себе греческий цифровой префикс, hendeca-, с Греческий суффикс -грамма. В hendeca- префикс происходит от греческого ἕνδεκα (ἕν + δέκα, один + десять), что означает "11". -грамма суффикс происходит от γραμμῆς (граммы) означает строку.[1]

Обычные хендкаграммы

Есть четыре обычные хендкаграммы,[2] которые можно описать обозначениями {11/2}, {11/3}, {11/4} и {11/5}; в этом обозначении число после косой черты указывает количество шагов между парами точек, соединенных ребрами. Эти же четыре формы можно рассматривать как звёздчатые регулярного девичник.[3]

Поскольку число 11 - простое число, все диаграммы представляют собой звездообразные многоугольники, а не составные фигуры.

Строительство

Как и в случае со всеми нечетными правильными многоугольниками и звездообразными многоугольниками, порядки которых не являются продуктами различных Простые числа Ферма, обычные диаграммы не могут быть построены с помощью циркуля и линейки.[4]Тем не мение, Хилтон и Педерсен (1986) опишите схемы складывания для создания хендкаграмм {11/3}, {11/4} и {11/5} из полосок бумаги.[5]

Приложения

Форт ВудЗвездные стены России стали основанием Статуи Свободы.

Призмы над диаграммами {11/3} и {11/4} могут использоваться для приближения формы ДНК молекулы.[6]

11-конечная звезда из Мавзолей Момине Хатун

Форт Вуд, теперь база Статуя Свободы в Нью-Йорк, это Звездный форт в виде неправильной 11-конечной звезды.[7]

В Свиток Топкапы содержит изображения 11-конечной звезды Гирих форма, используемая в Исламское искусство. Звезда в этом свитке не является одной из обычных форм хендекаграммы, но вместо этого использует линии, соединяющие вершины девичник к почти противоположным серединам краев пятиугольника.[8] Узоры с 11-конечной звездой Гирих также используются на внешней стороне Мавзолей Момине Хатун; Эрик Броуг пишет, что его узор «можно считать кульминацией исламского геометрического дизайна».[9]

11-конечное звездообразное поперечное сечение использовалось в Твердотопливный ракетный ускоритель космического корабля, для активной зоны носовой части ракеты (полое пространство, в котором горит топливо). Эта конструкция обеспечивала большую площадь поверхности и большую тягу на ранней стадии запуска, а также более низкую скорость горения и уменьшенную тягу после того, как концы звезды выгорели, примерно в то же время, когда ракета прошла мимо. звуковой барьер.[10]

Кроме того, Instagram использует синюю обычную диаграмму, чтобы различать проверенные страницы.

Смотрите также

Рекомендации

Звездные многоугольники
  1. ^ Лидделл, Генри Джордж; Скотт, Роберт (1940), Греко-английский лексикон: γραμμή, Оксфорд: Clarendon Press
  2. ^ O'Daffer, Phares G .; Клеменс, Стэнли Р. (1976), Геометрия: исследовательский подход, Эддисон-Уэсли, Упражнение 7, с. 62, ISBN 9780201054200.
  3. ^ Агрикола, Илька; Фридрих, Томас (2008), Элементарная геометрия, Студенческая математическая библиотека, 43, Американское математическое общество, п. 96, ISBN 9780821890677.
  4. ^ Карстенсен, Селин; Хорошо, Бенджамин; Розенбергер, Герхард (2011), Абстрактная алгебра: приложения к теории Галуа, алгебраической геометрии и криптографии, Сигма-ряд в чистой математике, 11, Вальтер де Грюйтер, п. 88, ISBN 9783110250084, С другой стороны, правильный 11-угольник не конструктивен.
  5. ^ Хилтон, Питер; Педерсен, Жан (1986), «Симметрия в математике», Компьютеры и математика с приложениями, 12 (1–2): 315–328, Дои:10.1016/0898-1221(86)90157-4, МИСТЕР 0838152
  6. ^ Яннер, Алоизио (июнь 2001 г.), «ДНК, включающая формы из масштабных форм роста снежных кристаллов», Кристалл Инжиниринг, 4 (2–3): 119–129, Дои:10.1016 / S1463-0184 (01) 00005-3
  7. ^ Адамс, Артур Г. (1996), Путеводитель по реке Гудзон, Fordham Univ Press, п. 66, ISBN 9780823216796.
  8. ^ Боднер, Б. Линн (2009), «Дизайн многоугольника с одиннадцатиконечной звездой. Свиток Топкапы", Мосты 2009: математика, музыка, искусство, архитектура, культура (PDF), стр. 147–154.
  9. ^ Броуг, Эрик (2013), Исламский геометрический дизайн, Темза и Гудзон, п. 182
  10. ^ Анджело, Джозеф А. (2009), Энциклопедия космоса и астрономии, Издание информационной базы, п. 511, г. ISBN 9781438110189.

внешняя ссылка