WikiDer > Октагемиоктаэдр

Октагемиоктаэдр
Тип	Равномерный звездный многогранник
Элементы	F = 12, E = 24 V = 12 (χ = 0)
Лица по сторонам	8{3}+4{6}
Символ Wythoff	3/2 3 | 3
Группа симметрии	Очас, [4,3], *432
Указатель ссылок	U03, C37, W68
Двойной многогранник	Октахемиоктакрон
Фигура вершины	3.6.3/2.6
Акроним Bowers	Охо

3D модель октагемиоктаэдра

В геометрия, то октагемиоктаэдр или же алллотетратраэдр это невыпуклый однородный многогранник, индексируется как U₃. Имеет 12 граней (8 треугольники и 4 шестиугольники), 24 ребра и 12 вершин.^[1] Его вершина фигуры это скрещенный четырехугольник.

Это один из девяти гемиполиэдры, с 4 шестиугольник грани, проходящие через центр модели.

Ориентируемость

Это единственный гемиполиэдр, который ориентируемый, и единственный равномерный многогранник с Эйлерова характеристика нуля (топологическая тор).

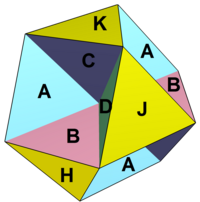Октагемиоктаэдр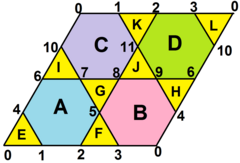

Топологическую сеть граней можно представить в виде ромб разделен на 8 треугольников и 4 шестиугольника. Все вершины угловые дефекты равны нулю.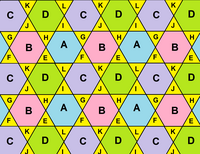

Сеть представляет собой область трехгексагональная черепица самолет.

Связанные многогранники

Он разделяет расположение вершин и расположение кромок с кубооктаэдр (имеющий общие треугольные грани), и с кубогемиоктаэдр (имеющий общие шестиугольные грани).

К Строительство Wythoff она имеет тетраэдрическая симметрия (Т_d), словно ромбитратраэдр строительство для кубооктаэдр, с чередующимися треугольниками с перевернутой ориентацией. Без чередующихся треугольников он имеет октаэдрическая симметрия (O_час).

Кубооктаэдр		Кубогемиоктаэдр	Октагемиоктаэдр
Октаэдрическая симметрия	Тетраэдрическая симметрия		Октаэдрическая симметрия	Тетраэдрическая симметрия
2 | 3 4	3 3 | 2	4/3 4 | 3 (двойная крышка)		3/2 3 | 3

Октахемиоктакрон

Октахемиоктакрон
Тип	Звездный многогранник
Лицо	—
Элементы	F = 12, E = 24 V = 12 (χ = 0)
Группа симметрии	Очас, [4,3], *432
Указатель ссылок	DU03
двойственный многогранник	Октагемиоктаэдр

В октагемиоктакрон является двойником октагемиоктаэдра и является одним из девяти двойные гемиполиэдры. Он визуально не отличается от гексагемиоктакрон.

Поскольку гемиполиэдры имеют лица проходя через центр, двойные фигуры иметь соответствующие вершины в бесконечности; правильно, на реальная проективная плоскость на бесконечности.^[2] В Магнус Веннингерс Двойные модели, они представлены пересекающимися призмы, каждая из которых продолжается в обоих направлениях до одной и той же бесконечно удаленной вершины, чтобы сохранить симметрию. На практике призмы модели обрезаются в удобном для производителя месте. Веннингер предположил, что эти фигуры принадлежат к новому классу людей. звездчатость цифры, называемые звёздчатость до бесконечности. Однако он также предположил, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.

Октагемиоктакрон имеет четыре вершины на бесконечности.

Смотрите также

• Соединение пяти октагемиоктаэдров
• Hemi-cube - Четыре бесконечно удаленные вершины соответствуют четырем вершинам этого абстрактного многогранника.

Рекомендации

• Веннингер, Магнус (2003) [1983], Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, МИСТЕР 0730208 (Стр. 101, Двойники (девяти) гемиполиэдров)

внешняя ссылка

• Эрик В. Вайсштейн, Октагемиоктаэдр (Равномерный многогранник) в MathWorld.
• Вайсштейн, Эрик В. «Октахемиоктакрон». MathWorld.
• Равномерные многогранники и двойники

Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. v т е