WikiDer > Квадратная плитка Тетракис
| Квадратная плитка Тетракис | |
|---|---|
 | |
| Тип | Двойной полурегулярный тайлинг |
| Лица | 45-45-90 треугольник |
| Диаграмма Кокстера | |
| Группа симметрии | p4m, [4,4], * 442 |
| Группа вращения | p4, [4,4]+, (442) |
| Двойной многогранник | Усеченная квадратная мозаика |
| Конфигурация лица | V4.8.8 |
| Характеристики | лицо переходный |
В геометрия, то квадратная плитка тетракис это мозаика Евклидова плоскость. Это квадратная черепица с каждым квадратом, разделенным на четыре равнобедренный прямоугольные треугольники от центральной точки, образуя бесконечное расположение линий. Его также можно сформировать путем деления каждого квадрата сетки на два треугольника по диагонали, при этом диагонали чередуются по направлению, или путем наложения двух квадратных сеток, одна из которых повернута на 45 градусов относительно другой и масштабирована с коэффициентом √2.
Конвей называет это кисвадриль,[1] представлен поцелуй операция, которая добавляет центральную точку и треугольники для замены граней квадратная черепица (кадриль). Его еще называют Решетка Юнион Джек из-за сходства с Флаг Великобритании треугольников, окружающих его вершины степени 8.[2]
Он помечен как V4.8.8, потому что каждая грань равнобедренного треугольника имеет два типа вершин: один с 4 треугольниками и два с 8 треугольниками.
Как двойная однородная мозаика
Это двойная тесселяция из усеченная квадратная мозаика который имеет один квадрат и два восьмиугольника в каждой вершине.[3]
Приложения
Часть квадратной плитки тетракис размером 5 × 9 используется для формирования доски для Малагасийский настольная игра Fanorona. В этой игре фигуры размещаются на вершинах мозаики и перемещаются по краям, захватывая части другого цвета, пока одна сторона не захватит все части другой стороны. В этой игре вершины мозаики степени 4 и степени 8 называются соответственно слабыми и сильными пересечениями, и это различие играет важную роль в стратегии игры.[4] Аналогичная плата также используется для Бразильский игра Адуго, и для игры Заяц и собаки.
Квадратная плитка тетракис использовалась для набора памятных почтовые марки выпущенный Почтовая служба Соединенных Штатов в 1997 году, с чередованием рисунков двух разных марок. По сравнению с более простым шаблоном для треугольных штампов, в котором все диагональные перфорации параллельны друг другу, шаблон тетракис имеет то преимущество, что при сгибании по любому из его перфораций другие перфорации выстраиваются друг с другом, делая возможным повторное складывание.[5]
Эта черепица также является основой для широко используемых узоров "вертушка", "ветряная мельница" и "битая посуда" в квилтинг.[6][7][8]
Симметрия
Тип симметрии:
- с расцветкой: см; а примитивная клетка это 8 треугольников, а фундаментальная область 2 треугольника (по 1/2 каждого цвета)
- с темными треугольниками черным и светлыми белыми: p4g; примитивная ячейка - это 8 треугольников, фундаментальная область - 1 треугольник (по 1/2 для черного и белого)
- с черными краями и белым интерьером: p4m; примитивная ячейка - это 2 треугольника, фундаментальная область 1/2
Края квадратной плитки тетракиса образуют симплициальное расположение линий, собственность, которую он разделяет с треугольная черепица и плитка кисромбиль.
Эти линии образуют оси симметрии из группа отражения (в группа обоев [4,4], (* 442) или p4m), в котором треугольники мозаики являются его фундаментальные области. Эта группа изоморфный к, но не то же самое, что и группа автоморфизмы мозаики, которая имеет дополнительные оси симметрии, разделяющие треугольники пополам, и полутреугольники в качестве основных областей.
Существует много подгрупп малого индекса симметрии p4m, [4,4] (* 442 орбифолдная запись), что можно увидеть по отношению к Диаграмма Кокстера, с узлами, окрашенными в соответствии с линиями отражения, и точками вращения, обозначенными численно. Вращательная симметрия показана попеременно белыми и синими областями, при этом одна основная область для каждой подгруппы залита желтым цветом. Скользящие отражения даны пунктирными линиями.
Подгруппы можно выразить как Диаграммы Кокстера, наряду с фундаментальными диаграммами доменов.
| Подгруппы малого индекса в p4m, [4,4], (* 442) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| индекс | 1 | 2 | 4 | ||||||||
| Фундаментальный домен диаграмма |  |  |  |  |  |  | |||||
| Обозначение Кокстера Диаграмма Кокстера | [1,4,1,4,1] = [4,4] | [1+,4,4] | [4,4,1+] | [4,1+,4] | [1+,4,4,1+] | [4+,4+] = [(4,4+,2+)] | |||||
| Орбифолд | *442 | *2222 | 22× | ||||||||
| Полупрямые подгруппы | |||||||||||
| индекс | 2 | 4 | |||||||||
| Диаграмма |  |  |  |  |  | ||||||
| Coxeter | [4,4+] | [4+,4] | [(4,4,2+)] | [1+,4,1+,4]=[(2+,4,4)] | [4,1+,4,1+]=[(4,4,2+)] | ||||||
| Орбифолд | 4*2 | 2*22 | |||||||||
| Прямые подгруппы | |||||||||||
| Индекс | 2 | 4 | 8 | ||||||||
| Диаграмма | 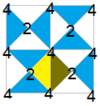 |  |  |  |  | ||||||
| Coxeter | [4,4]+ | [1+,4,4+] = [4,4+]+ | [4+,4,1+] = [4+,4]+ | [(4,1+,4,2+)] = [(4,4,2+)]+ | [1+,4,1+,4,1+] = [(4+,4+,2+)] = [4+,4+]+ | ||||||
| Орбифолд | 442 | 2222 | |||||||||
Смотрите также
Примечания
- ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 «Архивная копия». Архивировано из оригинал в 2010-09-19. Получено 2012-01-20.CS1 maint: заархивированная копия как заголовок (связь) (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, таблица с. 288)
- ^ Стивенсон, Джон, "Модель Изинга с антиферромагнитным взаимодействием ближайших соседей: спиновые корреляции и точки нарушения", Phys. Ред. B, 1 (11): 4405–4409, Дои:10.1103 / PhysRevB.1.4405.
- ^ Вайсштейн, Эрик В. «Двойная тесселяция». MathWorld.
- ^ Белл, Р.С. (1983), «Фанорона», Книга настольных игр, Exeter Books, стр. 150–151, ISBN 0-671-06030-9
- ^ Фредериксон, Грег Н. (2006), Фортепианные диссекции, А. К. Питерс, стр. 144.
- ^ Библия квилтинга, Creative Publishing International, 1997, стр. 55, ISBN 9780865732001.
- ^ Зиман, Нэнси (2011), Одеяло с уверенностью, Публикации Краузе, стр. 66, ISBN 9781440223556.
- ^ Фассетт, Каффе (2007), Калейдоскоп квилтов Каффе Фассетта: двадцать образцов из рябины для пэчворка и квилтинга, Тонтон Пресс, стр. 96, ISBN 9781561589388.
Рекомендации
| Викискладе есть медиафайлы по теме Квадратная плитка Тетракис. |
- Грюнбаум, Бранко И Шепард, Г.С. (1987). Плитки и узоры. Нью-Йорк: У. Х. Фриман. ISBN 0-7167-1193-1. (Глава 2.1: Регулярные и однородные мозаики, п. 58-65)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. стр. 40. ISBN 0-486-23729-X.
- Кит Кричлоу, Заказ в космосе: справочник по дизайну, 1970, с. 77-76, узор 8


