WikiDer > Восьмиугольная бипирамида - Википедия

Восьмиугольная бипирамида
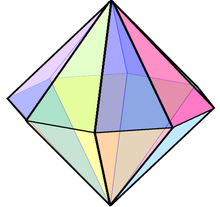Тип	бипирамида
Лица	16 треугольники
Края	24
Вершины	10
Символ Шлефли	{ } + {8}
Диаграмма Кокстера	;
Группа симметрии	D8ч, [8,2], (* 228), порядок 32
Группа вращения	D8, [8,2]+, (228), заказ 16
Двойной многогранник	восьмиугольная призма
Конфигурация лица	V4.4.8
Характеристики	выпуклый, лицо переходный

Octagonal bipyramid - Wikipedia

В восьмиугольная бипирамида один из бесконечного множества бипирамиды, двойственный бесконечности призмы. Если восьмиугольная бипирамида должна быть лицо переходный, все лица должны быть равнобедренные треугольники. 16-гранные кости часто представляют собой восьмиугольные бипирамиды.

Изображений

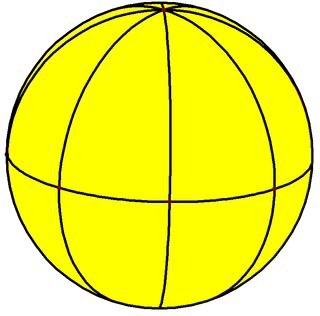
Его можно нарисовать как мозаику на сфере, которая также представляет фундаментальные области симметрии [4,2], * 422:

Связанные многогранники

«Обычное» правое (симметричное) п-гональный бипирамиды:
Имя	Дигональная бипирамида	Треугольная бипирамида (J₁₂)	Квадратная бипирамида (O)	Пятиугольная бипирамида (J₁₃)	Гексагональная бипирамида	Гептагональная бипирамида	Восьмиугольная бипирамида	Эннеагональная бипирамида	Десятиугольная бипирамида	...	Апейрогональная бипирамида
Многогранник изображение										...
Сферическая черепица изображение										Плоская черепица изображение
Конфигурация лица	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Диаграмма Кокстера										...

п42 мутации симметрии неусеченных мозаик: 4.8.2n* v т е
Симметрия *п42 [n, 4]	Сферический		Евклидово	Компактный гиперболический				Paracomp.
Симметрия *п42 [n, 4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Усеченный фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Усеченный двойники	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞