WikiDer > Автоэлектронная эмиссия
Автоэлектронная эмиссия, также известный как автоэлектронная эмиссия (FE) и электронная автоэлектронная эмиссия, это выброс электроны вызванный электростатическое поле. Наиболее распространенный контекст - автоэлектронная эмиссия твердый поверхность в вакуум. Однако автоэлектронная эмиссия может происходить от твердого тела или жидкость поверхности, в вакуум, жидкость (например. воздуха) или любой непроводящий или слабо проводящий диэлектрик. Полевое продвижение электронов из валентность к зона проводимости из полупроводники (в Эффект Зенера) также можно рассматривать как форму автоэлектронной эмиссии. Терминология историческая, потому что родственные явления поверхностного фотоэффекта, термоэлектронная эмиссия (или же Эффект Ричардсона – Душмана) и «холодная электронная эмиссия», то есть эмиссия электронов в сильных статических (или квазистатических) электрических полях, были открыты и исследованы независимо с 1880-х по 1930-е годы. Когда автоэлектронная эмиссия используется без квалификаторов, это обычно означает «холодная эмиссия».
Автоэмиссия в чистых металлах происходит в высоких электрические поля: градиенты обычно превышают 1 гигавольт на метр и сильно зависят от рабочая функция. Хотя источники электронов, основанные на автоэлектронной эмиссии, имеют ряд применений, автоэлектронная эмиссия чаще всего является нежелательным первичным источником вакуумный пробой и электрический разряд явления, над предотвращением которых работают инженеры. Примеры применения поверхностной автоэлектронной эмиссии включают создание источников ярких электронов для высокого разрешения. электронные микроскопы или разряд индуцированных зарядов от космический корабль. Устройства, устраняющие индуцированные заряды, называются нейтрализаторы заряда.
Автоэмиссия была объяснена квантовое туннелирование электронов в конце 1920-х гг. Это был один из триумфов зарождающегося квантовая механика. Теория автоэмиссии массивных металлов была предложена Ральф Х. Фаулер и Лотар Вольфганг Нордхайм.[1]Семейство приближенных уравнений, Уравнения Фаулера – Нордхейма, назван в их честь. Строго говоря, уравнения Фаулера – Нордхейма применимы только к автоэлектронной эмиссии массивных металлов и (с соответствующей модификацией) к другим объемным металлам. кристаллические твердые вещества, но они часто используются - в качестве грубого приближения - для описания полевой эмиссии из других материалов.
Терминология и условные обозначения
Автоэлектронная эмиссия, эмиссия электронов, индуцированная полем, автоэлектронная эмиссия и электронная автоэлектронная эмиссия - общие названия этого экспериментального явления и его теории. Здесь используется первое имя.
Туннель Фаулера – Нордхейма представляет собой волново-механическое туннелирование электронов через округлый треугольный барьер, создаваемый на поверхности электронного проводника путем приложения очень сильного электрического поля. Отдельные электроны могут ускользать через туннелирование Фаулера-Нордхейма из многих материалов в различных условиях.
Электронная эмиссия холодного поля (CFE) - это название, данное определенному режиму статистической эмиссии, в котором электроны в эмиттере изначально находятся во внутренних термодинамическое равновесие, и в котором большинство эмитированных электронов ускользают в результате туннелирования Фаулера-Нордхейма из электронных состояний, близких к эмиттеру. Уровень Ферми. (Напротив, в Эмиссия Шоттки В режиме CFE большинство электронов ускользает через барьер с уменьшенным полем из состояний, значительно превышающих уровень Ферми.) Многие твердые и жидкие материалы могут испускать электроны в режиме CFE, если приложено электрическое поле подходящего размера.
Уравнения типа Фаулера – Нордхейма представляют собой семейство приближенных уравнений, полученных для описания CFE из внутренних электронных состояний в объемных металлах. Различные члены семьи представляют разные степени приближения к реальности. Приближенные уравнения необходимы, потому что для физически реалистичных моделей туннельного барьера математически невозможно в принципе решить Уравнение Шредингера ровно любым простым способом. Нет теоретических оснований полагать, что уравнения типа Фаулера-Нордхейма достоверно описывают полевую эмиссию материалов, отличных от объемных кристаллических твердых тел.
Для металлов режим CFE простирается до температур значительно выше комнатной. Существуют и другие режимы электронной эмиссии (например, "тепловая электронная эмиссия" и "Эмиссия Шоттки"), которые требуют значительного внешнего нагрева эмиттера. Существуют также режимы эмиссии, при которых внутренние электроны не находятся в термодинамическом равновесии, а ток эмиссии, частично или полностью, определяется подачей электронов в излучающую область. Неравновесный Процесс эмиссии такого типа можно назвать полевой (электронной) эмиссией, если большая часть электронов ускользает путем туннелирования, но строго говоря, это не CFE и не точно описывается уравнением типа Фаулера-Нордхейма.
Необходима осторожность, потому что в некоторых контекстах (например, в космической технике) название «полевая эмиссия» применяется к вызванной полем эмиссии ионов (полевая эмиссия ионов), а не электронов, и потому что в некоторых теоретических контекстах «полевая эмиссия» является используется как общее название, охватывающее как полевую электронную эмиссию, так и полевую эмиссию ионов.
Исторически явление автоэлектронной эмиссии было известно под разными названиями, включая «эффект аэоны», «автоэлектронная эмиссия», «холодная эмиссия», «эмиссия с холодным катодом», «полевая эмиссия», «полевая эмиссия электронов». и «автоэлектронная эмиссия».
Уравнения в этой статье написаны с использованием Международная система количеств (ISQ). Это современная (после 1970-х годов) международная система, основанная на системе уравнений рационализированный метр-килограмм-секунда (rmks), которая используется для определения единиц СИ. В более старой литературе по автоэмиссии (и в статьях, которые напрямую копируют уравнения из старой литературы) часто пишутся некоторые уравнения с использованием более старой системы уравнений, в которой не используется величина ε0. В этой статье все такие уравнения были преобразованы в современную международную форму. Для наглядности это нужно делать всегда.
Поскольку работа выхода обычно указывается в электронвольтах (эВ), и часто бывает удобно измерять поля в вольтах на нанометр (В / нм), значения большинства универсальных констант приведены здесь в единицах, включающих эВ, В и нм. Все чаще это нормальная практика в исследованиях полевых выбросов. Однако все уравнения здесь являются уравнениями, совместимыми с ISQ, и остаются согласованными по размерам, как того требует современная международная система. Для обозначения их статуса числовые значения универсальных констант приведены до семи значащих цифр. Значения получены с использованием значений фундаментальных констант за 2006 год.
Ранняя история автоэлектронной эмиссии
Автоэлектронная эмиссия имеет долгую, сложную и запутанную историю. Этот раздел охватывает раннюю историю, вплоть до вывода исходного уравнения типа Фаулера – Нордхейма в 1928 году.
Оглядываясь назад, кажется вероятным, что электрические разряды, о которых сообщил Винклер,[2] в 1744 г. были начаты ДОВСЕ с его проволочного электрода. Однако значимые расследования пришлось отложить до J.J. Томсонс[3] идентификация электрона в 1897 году, и до тех пор, пока это не было понято - с тепловое излучение[4] и фотоэмиссия[5] работа - электроны могут испускаться изнутри металлов (а не из молекулы газа, адсорбированные на поверхности), и что в отсутствие приложенных полей электроны, вылетающие из металлов, должны преодолевать барьер работы выхода.
Еще в 1913 году предполагалось, что индуцированная полем эмиссия представляет собой отдельный физический эффект.[6] Однако только после того, как методы вакуумирования и очистки образцов были значительно улучшены, это стало прочно обоснованным. Лилиенфельд (кого в первую очередь интересовали источники электронов для медицинских рентгеновский снимок приложений) опубликовано в 1922 г.[7] первое ясное изложение на английском языке экспериментальной феноменологии эффекта, который он назвал «автоэлектронная эмиссия». Он работал над этой темой в Лейпциге примерно с 1910 года. Кляйнт описывает эту и другие ранние работы.[8][9]
После 1922 г. экспериментальный интерес возрос, особенно в группах под руководством Милликен в Калифорнийском технологическом институте (Caltech) в Пасадена, Калифорния,[10] и Госслинг в Компания General Electric В Лондоне.[11] Попытки понять автоэлектронную эмиссию включали построение экспериментальных вольт-амперных графиков (i – V) данных по-разному, чтобы найти прямую связь. Ток увеличивался с увеличением напряжения быстрее, чем линейно, но графики типа log (я) против. V не были прямыми.[10] Шоттки[12] предположил в 1923 г., что эффект может быть вызван термически индуцированным излучением через барьер с уменьшенным полем. Если да, то графики журнала (я) против. √V должны быть прямыми, но их не было.[10] Объяснение Шоттки также несовместимо с экспериментальным наблюдением лишь очень слабой температурной зависимости CFE.[7] - момент, изначально упущенный из виду.[6]
Прорыв произошел, когда Лауритсен[13](и Оппенгеймер независимо[14]) обнаружил, что графики журнала (я) vs. 1 /V дали хорошие прямые. Этот результат, опубликованный Милликеном и Лауритсеном[13] в начале 1928 г. Фаулер и Nordheim.
Оппенгеймер предсказал[14] что индуцированное полем туннелирование электронов от атомов (эффект, теперь называемый полевой ионизацией) будет иметь это я(V), нашел эту зависимость в опубликованных экспериментальных результатах полевой эмиссии Милликена и Эйринга,[10] и предположил, что CFE был вызван индуцированным полем туннелирование электронов с атомных орбиталей в поверхностных атомах металла. Альтернативная теория Фаулера – Нордхейма.[1] объяснил как открытие Милликена-Лауритсена, так и очень слабую зависимость тока от температуры. Теория Фаулера-Нордхейма предсказывала, что оба они будут следствием, если CFE будет происходить из-за индуцированного полем туннелирования состояния типа свободных электронов в том, что мы бы сейчас назвали металлом зона проводимости, причем электронные состояния заняты в соответствии с Статистика Ферми – Дирака.
У Оппенгеймера математические детали своей теории были серьезно неверны.[15] Также была небольшая численная ошибка в окончательном уравнении теории Фаулера-Нордхейма для CFE плотность тока: это было исправлено в статье 1929 года (Стерн, Госслинг и Фаулер 1929).[16]
Строго говоря, если барьерное поле в теории Фаулера-Нордхейма 1928 года точно пропорционально приложенному напряжению, и если площадь излучения не зависит от напряжения, то теория Фаулера-Нордхейма 1928 года предсказывает, что графики формы (log (я/V2) vs. 1 /V) должны быть точными прямыми линиями. Однако современные экспериментальные методы были недостаточно хороши, чтобы отличить теоретический результат Фаулера-Нордхейма от экспериментального результата Милликена-Лауритсена.
Таким образом, к 1928 г. было достигнуто основное физическое понимание происхождения CFE из массивных металлов и было выведено исходное уравнение типа Фаулера-Нордхейма.
В литературе часто представлены работы Фаулера-Нордхейма как доказательства существования электронное туннелирование, как предсказывает волновая механика. Хотя это и верно, к 1928 году волновая механика была в значительной степени признана. Более важная роль статьи Фаулера-Нордхейма заключалась в том, что это был убедительный экспериментальный аргумент. Статистика Ферми – Дирака применительно к поведению электронов в металлах, как предполагает Зоммерфельд[17] в 1927 г. Успех теории Фаулера-Нордхейма во многом поддержал правильность идей Зоммерфельда и во многом помог установить современные электронная зонная теория.[18] В частности, исходное уравнение типа Фаулера-Нордхейма было одним из первых, в котором статистико-механический последствия существования спин электрона в теорию экспериментального эффекта конденсированной среды. В статье Фаулера-Нордхейма также была установлена физическая основа для единой трактовки индуцированных полем и термически индуцированная электронная эмиссия.[18] До 1928 года была выдвинута гипотеза, что в металлах существуют два типа электронов, «термоэлектроны» и «электроны проводимости», и что термически испускаемые электронные токи возникают из-за испускания термоэлементов, но что полевые токи возникают из-за испускание электронов проводимости. В работе Фаулера-Нордхейма 1928 г. было высказано предположение, что термионы не обязательно должны существовать как отдельный класс внутренних электронов: электроны могут происходить из одного группа занята в соответствии со статистикой Ферми – Дирака, но будет испускаться статистически по-разному при различных условиях температуры и приложенного поля.
Идеи Оппенгеймер, Фаулер и Nordheim также были важным стимулом для развития, Гамов,[19] и Герни и Кондон,[20][21] позже, в 1928 г., теории радиоактивный распад ядер (по альфа-частица туннелирование).[22]
Практическое применение: прошлое и настоящее
Как уже указывалось, ранние экспериментальные работы по автоэлектронной эмиссии (1910–1920 гг.)[7] был движим Лилиенфельда желание развиваться в миниатюре рентгеновский снимок трубки для медицинского применения. Однако преуспевать этой технологии было еще рано.
После теоретической работы Фаулера-Нордхайма в 1928 году значительный прорыв произошел с разработкой в 1937 году Эрвин В. Мюллер сферической геометрии полевой электронный микроскоп (FEM)[23] (также называемый «автоэмиссионным микроскопом»). В этом приборе эмиттер электронов представляет собой остроконечный провод с радиусом вершины. р. Он помещается в вакуумный кожух напротив детектора изображения (первоначально люминофорный экран) на расстоянии р от него. На экране микроскопа отображается проекционное изображение распределения плотности тока. J поперек вершины излучателя, с увеличением примерно (р/р), обычно 105 до 106. В исследованиях МКЭ радиус вершины обычно составляет от 100 нм до 1 мкм. Кончик заостренного провода, когда его называют физическим объектом, был назван «полевым эмиттером», «острием» или (недавно) «эмиттером Мюллера».
Когда поверхность эмиттера чистая, это изображение МКЭ характерно для: (а) материала, из которого изготовлен эмиттер: (б) ориентации материала относительно оси игла / проволока; и (c) до некоторой степени форма торцевой формы эмиттера. На изображении МКЭ темные области соответствуют областям, где локальная работа выхода φ относительно высокое и / или локальное барьерное поле F относительно низкий, поэтому J относительно невысокий; светлые области соответствуют областям, где φ относительно низкий и / или F относительно высокий, поэтому J относительно высокий. Это предсказывается показателем степени уравнений типа Фаулера-Нордхейма [см. (30) ниже].
В адсорбция слоев атомов газа (например, кислорода) на поверхности эмиттера или его части, может создавать поверхность электрические диполи которые изменяют локальную работу выхода этой части поверхности. Это влияет на изображение FEM; Кроме того, изменение работы выхода можно измерить с помощью графика Фаулера-Нордхейма (см. ниже). Таким образом, МКЭ стал одним из первых инструментов наблюдения наука о поверхности.[24][25] Например, в 1960-х годах результаты МКЭ внесли значительный вклад в дискуссии о гетерогенный катализ.[26] МКЭ также использовался для исследования диффузия поверхностных атомов. Однако сейчас МКЭ почти полностью вытеснен новыми методами исследования поверхности.
Следствием разработки МКЭ и последующих экспериментов стало то, что стало возможным идентифицировать (по проверке изображения МКЭ), когда излучатель был «чистым» и, следовательно, проявлял свою работу выхода с чистой поверхностью, как установлено другими методами. Это было важно в экспериментах, направленных на проверку правильности стандартного уравнения типа Фаулера-Нордхейма.[27][28] Эти эксперименты позволили установить значение коэффициента преобразования напряжения в барьерное поле. β из графика Фаулера-Нордхейма (см. ниже), предполагая, что чистая поверхность φ–Значение для вольфрама, и сравнив его со значениями, полученными из электронный микроскоп наблюдения за формой излучателя и электростатическое моделирование. Достигнута договоренность с точностью до 10%. Только совсем недавно[29] Можно ли было провести сравнение в обратном порядке, поднеся хорошо подготовленный зонд так близко к хорошо подготовленной поверхности, что можно предположить приблизительную геометрию параллельных пластин, а коэффициент преобразования можно принять равным 1 /W, куда W - измеренное расстояние между зондом и эмиттером. Анализ полученного графика Фаулера-Нордхейма дает значение работы выхода, близкое к независимо известной работе выхода эмиттера.
Полевая электронная спектроскопия (анализ энергии электронов)
Впервые об измерениях распределения энергии полевых электронов было сообщено в 1939 году.[30] В 1959 году это было теоретически реализовано Янгом,[31] и подтверждено экспериментально Янгом и Мюллером[32] что величина, измеренная в сферической геометрии, была распределением полной энергии испущенного электрона (его «распределением полной энергии»). Это потому, что в сферической геометрии электроны движутся таким образом, что угловой момент около точки в эмиттере почти сохраняется. Следовательно, любой кинетическая энергия который при излучении находится в направлении, параллельном поверхности эмиттера, преобразуется в энергию, связанную с радиальным направлением движения. Таким образом, анализатор энергии измеряет полная энергия при выбросе.
С появлением в 1960-х годах чувствительных электронных анализаторов энергии стало возможным измерять мельчайшие детали распределения полной энергии. Они отражают мелкие детали физика поверхности, и техника полевой электронной спектроскопии некоторое время процветала, прежде чем ее вытеснили более новые методы исследования поверхности.[33][34]
Полевые эмиттеры электронов как источники электронной пушки

Для достижения высокого разрешения в электронные микроскопы и другие электронно-лучевые приборы (например, используемые для электронно-лучевая литография), полезно начать с небольшого, оптически яркого и стабильного источника электронов. Источники, основанные на геометрии излучателя Мюллера, хорошо подходят по первым двум критериям. Первый электронный микроскоп (ЭМ) наблюдение отдельного атома было сделано Крю, Уоллом и Лэнгмором в 1970 г.[35] используя растровый электронный микроскоп оснащен ранней автоэмиссионной пушкой.
Начиная с 1950-х годов, значительные усилия были направлены на разработку источников полевой эмиссии для использования в электронные пушки.[36][37][38] [например, DD53] Были разработаны методы генерации осевых лучей либо за счет нарастания эмиттера, индуцированного полем, либо путем выборочного осаждения с низкой работой выхода. адсорбат (обычно Оксид циркония - ZrO) в плоскую вершину (100) ориентированные Вольфрам эмиттер.[39]
Источники, работающие при комнатной температуре, обладают тем недостатком, что они быстро покрываются адсорбатом. молекулы которые прибывают из вакуум стенки системы, а эмиттер необходимо время от времени очищать «прошивкой» до высокой температуры. В настоящее время более распространено использование источников на основе излучателя Мюллера, которые работают при повышенных температурах, либо в Эмиссия Шоттки режиме или в так называемом промежуточном режиме температурного поля. Многие современные электронные микроскопы высокого разрешения и электронно-лучевые приборы используют тот или иной вид источника электронов на основе эмиттера Мюллера. В настоящее время делаются попытки разработать углеродные нанотрубки (УНТ) как источники автоэлектронной эмиссии.[40][41]
Использование источников автоэмиссии в электронно-оптических приборах потребовало развития соответствующих теорий оптики заряженных частиц.[37][42] и развитие связанного моделирования. Для эмиттеров Мюллера были опробованы различные модели формы; Лучшей кажется модель «Сфера на ортогональном конусе» (SOC), представленная Дайком, Троланом. Долан и Барнс в 1953 году.[43] Важное моделирование, включающее отслеживание траектории с использованием модели излучателя SOC, было выполнено Визенером и Эверхартом.[44][45][46] В настоящее время средство для моделирования полевой эмиссии излучателей Мюллера часто включается в коммерческие программы электронной оптики, используемые для разработки электронно-лучевых приборов. Создание эффективных современных автоэмиссионных электронных пушек требует высокоспециализированных знаний.
Атомно-резкие излучатели
В настоящее время можно изготовить очень острые эмиттеры, в том числе эмиттеры, оканчивающиеся на один атом. В этом случае электронная эмиссия исходит из области, примерно вдвое превышающей кристаллографический размер одиночного атома. Это было продемонстрировано путем сравнения МКЭ и полевой ионный микроскоп (FIM) изображения излучателя.[47] Эмиттеры Мюллера с одним атомом вершины также имеют отношение к сканирующая зондовая микроскопия и гелиевая сканирующая ионная микроскопия (Он СИМ).[48] Методы их приготовления изучаются в течение многих лет.[47][49] Связанным важным недавним достижением стала разработка (для использования в He SIM) автоматизированной техники восстановления трехатомного («тримерного») апекса в его исходное состояние, если тример разрушается.[48]
Источники автоэмиссии большой площади: вакуумная наноэлектроника
Аспекты материалов
Источники полевой эмиссии с большой площадью представляют интерес с 1970-х годов. В этих устройствах высокая плотность отдельных участков автоэмиссии создается на подложке (первоначально кремнии). Это направление исследований стало известно сначала как «вакуумная микроэлектроника», а теперь как «вакуумная наноэлектроника».
Один из двух исходных типов устройств, "Массив шпиндта",[50] использовал кремниевая интегральная схема (IC) методы изготовления для изготовления регулярных массивов, в которых молибден Конусы осаждались в небольших цилиндрических пустотах в оксидной пленке, причем пустоты закрывались противоэлектродом с центральной круглой апертурой. Эта общая геометрия также использовалась с углеродные нанотрубки выросли в пустоте.
Другим оригинальным типом устройств был «излучатель Latham».[51][52] Это были MIMIV (металл-изолятор-металл-изолятор-вакуум) или, в более общем смысле, CDCDV (проводник-диэлектрик-проводник-диэлектрик-вакуум) - устройства, которые содержали проводящие частицы в диэлектрической пленке. Устройство излучает поле, потому что его микроструктура / наноструктура обладает улучшающими поле свойствами. Этот материал имел потенциальное производственное преимущество, так как его можно было наносить в виде «чернил», поэтому технологии изготовления ИС не требовались. Однако на практике оказалось трудно изготовить неизменно надежные устройства.
Были продвинуты исследования по поиску других материалов, которые можно было бы осаждать / выращивать в виде тонких пленок с подходящими полевыми свойствами. При расположении параллельных пластин "макроскопическое" поле FM между пластинами задается FM = V/W, куда W это расстояние между пластинами и V приложенное напряжение. Если на одной пластине создается острый предмет, то локальное поле F на его вершине больше чем FM и может быть связано с FM к
Параметр γ называется «коэффициентом усиления поля» и в основном определяется формой объекта. Поскольку характеристики автоэмиссии определяются локальным полем F, то чем выше γ-значение объекта, чем ниже значение FM при котором происходит значительная эмиссия. Следовательно, для данного значения W, чем ниже приложенное напряжение V при котором происходит значительная эмиссия.
В течение примерно десяти лет с середины 1990-х годов был большой интерес к автоэлектронной эмиссии из пленок, осажденных плазмой. аморфный и «алмазоподобный» углерод.[53][54] Однако впоследствии интерес снизился, отчасти из-за прибытия CNT источников, и отчасти потому, что появились доказательства того, что места выбросов могут быть связаны с твердыми частицами углерода, созданными неизвестным образом во время процесс осаждения: это предполагает, что контроль качества процесса производства в промышленных масштабах может быть проблематичным.
Внедрение полевых эмиттеров УНТ,[41] как в «матовой» форме, так и в «выращиваемой» форме, было значительным шагом вперед. Были проведены обширные исследования как их физических характеристик, так и возможных технологических применений.[40] Для автоэлектронной эмиссии преимущество УНТ состоит в том, что из-за их формы с высокой соотношение сторон, они являются «естественными объектами, усиливающими поле».
В последние годы также наблюдается значительный рост интереса к разработке других форм тонкопленочных эмиттеров, основанных на других формах углерода (таких как «углеродные наностенки»).[55] ") и на различных формах широкозонных полупроводников.[56] Конкретная цель - разработать "высокоэффективныеγ«наноструктуры с достаточно высокой плотностью индивидуальных эмиссионных центров. Тонкие пленки нанотрубки в виде полотен нанотрубок также используются для разработки автоэмиссионных электродов.[57][58][59] Показано, что за счет точной настройки параметров изготовления эти полотна могут достигать оптимальной плотности отдельных участков излучения.[57] Показано, что двухслойные электроды, полученные осаждением двух слоев этих полотен с перпендикулярным расположением друг к другу, способны снизить электрическое поле включения (электрическое поле, необходимое для достижения тока эмиссии 10 мкА / см2) до 0,3 В / мкм и обеспечивают стабильную автоэмиссию.[58]
Общие проблемы со всеми автоэмиссионными устройствами, особенно теми, которые работают в «промышленных условиях вакуума», заключаются в том, что характеристики излучения могут ухудшаться из-за адсорбции атомов газа, поступающих из других частей системы, а форма эмиттера в принципе может быть существенно изменена. за счет множества нежелательных дополнительных процессов, таких как бомбардировка ионами, создаваемыми ударами испускаемых электронов на атомы газовой фазы и / или на поверхность противоэлектродов. Таким образом, важным промышленным требованием является «надежность в условиях плохого вакуума»; это необходимо учитывать при исследованиях новых эмиттерных материалов.
На момент написания наиболее многообещающими формами источников автоэлектронной эмиссии большой площади (определенно с точки зрения достигнутой средней плотности тока эмиссии) представлялись Массивы шпиндта и различные формы источников на основе УНТ.
Приложения
Разработка источников полевой эмиссии с большой площадью первоначально была вызвана желанием создать новые, более эффективные формы электронный информационный дисплей. Они известны как "автоэмиссионные дисплеи"или" наноэмиссионные дисплеи ". Хотя было продемонстрировано несколько прототипов,[40] Превращению таких дисплеев в надежные коммерческие продукты препятствовали различные проблемы промышленного производства, не связанные напрямую с характеристиками источника [En08].
Другие предлагаемые применения источников полевой эмиссии большой площади[40] включают микроволновая печь генерация, нейтрализация космических аппаратов, Рентгеновское излучение, и (для источников массива) несколько электронно-лучевая литография. Также в последнее время предпринимаются попытки разработать излучатели большой площади на гибких подложках в соответствии с более широкими тенденциями к "пластиковая электроника".
Разработка таких приложений - миссия вакуумной наноэлектроники. Однако полевые эмиттеры лучше всего работают в условиях хорошего сверхвысокого вакуума. Их наиболее успешное применение на сегодняшний день (пистолеты МКЭ, ФЭС и ЭМ) приходятся на эти условия. Печальный факт остается фактом: полевые эмиттеры и условия промышленного вакуума плохо сочетаются друг с другом, и связанные с этим проблемы надежного обеспечения хорошей «вакуумной устойчивости» источников автоэмиссии, используемых в таких условиях, все еще ждут лучших решений (возможно, более умных материалов), чем мы в настоящее время имеют.
Вакуумный пробой и явления электрического разряда
Как уже указывалось, теперь считается, что самыми ранними проявлениями полевой электронной эмиссии были вызванные ею электрические разряды. После работы Фаулера-Нордхейма стало понятно, что CFE была одной из возможных основных причин пробоя вакуума и явления электрического разряда. (Детально описанные механизмы и пути могут быть очень сложными, и единой универсальной причины не существует)[60] Если известно, что пробой вакуума вызван эмиссией электронов из катода, то первоначально предполагалось, что механизмом является CFE из небольших проводящих игольчатых выступов на поверхности. Процедуры использовались (и используются) для округления и сглаживания поверхностей электродов, которые могут генерировать нежелательные токи полевой электронной эмиссии. Однако работа Латама и других[51] показали, что эмиссия также может быть связана с наличием полупроводниковых включений на гладких поверхностях. Физика того, как генерируется излучение, до сих пор полностью не изучена, но есть подозрения, что могут быть задействованы так называемые «эффекты тройного перехода». Дополнительную информацию можно найти в книге Латама.[51] и в интерактивной библиографии.[60]
Внутренний перенос электронов в электронных устройствах
В некоторых электронных устройствах перенос электронов от одного материала к другому или (в случае наклонных полос) от одной полосы к другой ("Зинеровское туннелирование"), происходит в результате индуцированного полем процесса туннелирования, который можно рассматривать как форму туннелирования Фаулера-Нордхейма. Например, Родерика книга обсуждает теорию, относящуюся к контакты металл-полупроводник.[61]
Туннель Фаулера – Нордхейма
Вступление
Следующая часть статьи посвящена основам теории холодной автоэлектронной эмиссии массивных металлов. Лучше всего рассматривать это в четыре основных этапа, включая теорию, связанную с: (1) выводом формулы для "вероятность побега", С учетом электронное туннелирование через округло-треугольный барьер; (2) интегрирование по внутренним электронным состояниям для получения «распределения полной энергии»; (3) второе интегрирование для получения плотности тока эмиссии как функции локального барьерного поля и локальной работы выхода; (4) преобразование этого в формулу для тока как функции приложенного напряжения. Модифицированные уравнения, необходимые для излучателей большой площади, и вопросы анализа экспериментальных данных рассматриваются отдельно.
Туннель Фаулера – Нордхейма - это волново-механическое туннелирование электрона через точный или округлый треугольный барьер. Различают две основные ситуации: (1) когда электрон изначально находится в локализованное состояние; (2) когда электрон изначально не сильно локализован и лучше всего представлен бегущая волна. Выбросы от насыпного металла зона проводимости это ситуация второго типа, и обсуждение здесь относится к этому случаю. Также предполагается, что барьер является одномерным (т.е. не имеет боковой структуры) и не имеет мелкомасштабной структуры, которая вызывает "рассеяние"или" резонансные "эффекты. Чтобы сделать это объяснение туннелирования Фаулера-Нордхейма относительно простым, необходимы эти допущения, но атомная структура материи в действительности игнорируется.
Движущая энергия
Для электрона одномерная Уравнение Шредингера можно записать в виде
где Ψ (Икс) - электрон волновая функция, выраженная как функция расстояния Икс измеряется от электрической поверхности излучателя,[62] час это приведенная постоянная Планка, м - масса электрона, U(Икс) это потенциальная энергия электрона, Eп это полная энергия электронов связанных с движением в Икс-направление, и M(Икс) = [U(Икс) − Eп] называется движущей энергией электрона.[63] M(Икс) можно интерпретировать как отрицательную величину кинетической энергии электрона, связанную с движением гипотетического классического точечного электрона в Икс-направление, а в барьере - положительное.
Форма туннельного барьера определяется тем, как M(Икс) меняется в зависимости от положения в регионе, где M(Икс)> 0. Две модели имеют особый статус в теории автоэмиссии: точный треугольный (ET) барьер и Барьер Шоттки – Нордхейма (SN).[64][65] Они задаются уравнениями (2) и (3) соответственно:
Здесь час высота нулевого поля (или неуменьшенная высота) барьера, е это элементарный положительный заряд, F - барьерное поле, а ε0 это электрическая постоянная. Условно, F воспринимается как положительный, хотя классическое электростатическое поле будет отрицательным. Уравнение SN использует классическую потенциальную энергию изображения для представления физического эффекта «корреляции и обмена».
Вероятность побега
Для электрона, приближающегося к заданному барьеру изнутри, вероятность побега (или же "коэффициент передачи"или" коэффициент проникновения ") является функцией час и F, и обозначается D(час,F). Основная цель теории туннелирования - вычислить D(час,F). Для физически реалистичных моделей барьеров, таких как барьер Шоттки-Нордхейма, Уравнение Шредингера не может быть решена каким-либо простым способом. Можно использовать следующий так называемый «полуклассический» подход. Параметр грамм(час,F) можно определить как JWKB (Джеффрис-Вентцель-Крамерс-Бриллюэн) интеграл:[66]
где интеграл берется через барьер (т. е. через область, где M > 0), а параметр грамм - универсальная постоянная, задаваемая формулой
Форбс изменил результат, доказанный Фроманом и Фроманом, чтобы показать, что формально - в одномерном рассмотрении - точное решение для D можно написать[67]
где предварительный фактор туннелирования п в принципе можно оценить путем сложных итерационных интеграций по пути в сложное пространство.[67][68] В режиме ДОВСЕ мы имеем (по определению) грамм ≫ 1. Также для простых моделей п ≈ 1. Итак, ур. (6) сводится к так называемому простому JWKB формула:
Для точного треугольного барьера, положив ур. (2) в ур. (4) дает граммET = бх3/2/F, куда
Этот параметр б универсальная константа, которую иногда называют вторая постоянная Фаулера – Нордхейма. Для барьеров другой формы пишем
куда ν(час,F) является поправочным коэффициентом, который обычно определяется численное интегрирование, используя ур. (4).
Поправочный коэффициент для барьера Шоттки – Нордхейма
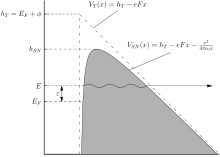
Барьер Шоттки-Нордхейма, который является моделью барьера, используемой при выводе стандартного уравнения типа Фаулера-Нордхейма,[69] это особый случай. В этом случае известно, что поправочный коэффициент является функцией одной переменной жчас, определяется жчас = F/Fчас, куда Fчас поле, необходимое для уменьшения высоты барьера Шоттки – Нордхейма с час в 0. Это поле определяется как
Параметр жчас работает от 0 до 1 и может быть назван масштабное барьерное поле, для барьера Шоттки-Нордхейма нулевой высоты поля час.
Для барьера Шоттки – Нордхейма ν(час,F) дается конкретным значением ν(жчас) функции ν(ℓ ′). Последняя является самостоятельной функцией математической физики и получила название основная барьерная функция Шоттки – Нордхейма. Явное разложение в ряд для ν(ℓ ′) получен в статье Дж. Дина в 2008 году.[70] Следующее хорошее простое приближение для ν(жчас) был найден:[69]
Ширина распада
В ширина распада (по энергии), dчас, измеряет, насколько быстро вероятность побега D уменьшается с высотой барьера час увеличивается; dчас определяется:
Когда час увеличивается на dчас тогда вероятность побега D уменьшается в раз, близкий к e (≈ 2.718282). Для элементарной модели, основанной на точном треугольном барьере, где положим ν = 1 и п ≈ 1, получаем
Ширина распада dчас полученное из более общего выражения (12) отличается от него "поправочным коэффициентом ширины спада" λd, так:
Обычно поправочный коэффициент приближается к единице.
Ширина распада dF для барьера с час равняется локальной работе выхода φ представляет особый интерес. Численно это определяется как:
Для металлов значение dF обычно порядка 0,2 эВ, но зависит от барьерного поля. F.
Комментарии
Историческая справка необходима. Идея о том, что барьер Шоттки-Нордхейма нуждается в поправочном коэффициенте, как в ур. (9), была введена Нордхеймом в 1928 г.,[65] но его математический анализ фактора был неверным. Бёрджесс ввел новую (правильную) функцию: Кремер и Хьюстон[71] в 1953 году, а его математика была развита Мерфи и Гудом в 1956 году.[72] Эта скорректированная функция, иногда известная как «специальная эллиптическая функция автоэлектронной эмиссии», была выражена как функция математической переменной у известный как «параметр Нордхейма». Лишь недавно (с 2006 по 2008 год) стало ясно, что математически гораздо лучше использовать переменную ℓ ′ ( = у2). И только недавно удалось завершить определение ν(ℓ ′) путем разработки и доказательства справедливости разложения в точный ряд для этой функции (исходя из известных частных решений уравнения Гаусса гипергеометрическое дифференциальное уравнение). К тому же приближение (11) было найдено совсем недавно. Приближение (11) превосходит все более старые приближения эквивалентной сложности и, вероятно, в конечном итоге вытеснит их. Эти недавние разработки и их последствия, вероятно, со временем окажут значительное влияние на исследования полевых выбросов.
Следующее резюме объединяет эти результаты. Для туннелей значительно ниже вершины хорошо оборудованного барьера разумной высоты вероятность выхода D(час,F) дается формально:
куда ν(час,F) является поправочным коэффициентом, который обычно определяется численным интегрированием. Для частного случая барьера Шоттки-Нордхейма существует аналитический результат и ν(час,F) дан кем-то ν(жчас), как обсуждалось выше; приближение (11) для ν(жчас) более чем достаточно для всех технологических целей. Предварительный фактор п также в принципе является функцией час и возможно) F, но для обсуждаемых здесь простых физических моделей обычно достаточно приближения п = 1. Точный треугольный барьер - частный случай, когда Уравнение Шредингера можно решить точно, как это сделали Фаулер и Нордхейм;[1] для этого физически нереального случая, ν(жчас) = 1, и аналитическое приближение для п существуют.
Описанный здесь подход был первоначально разработан для описания туннелирования Фаулера – Нордхейма с гладких, классически плоских плоских излучающих поверхностей. Он подходит для гладких классических изогнутых поверхностей с радиусом от 10 до 20 нм. Его можно адаптировать к поверхностям с более острым радиусом, но такие количества, как ν и D затем становятся важными функциями параметра (ов), используемых для описания кривизны поверхности. Когда эмиттер настолько резкий, что нельзя пренебречь деталями на атомном уровне, и / или туннельный барьер толще, чем размеры вершины эмиттера, тогда желателен более сложный подход.
Как отмечалось в начале, влияние атомной структуры материалов не принимается во внимание в относительно простых трактовках автоэлектронной эмиссии, обсуждаемых здесь. Правильный учет атомной структуры - очень трудная проблема, и достигнут лишь ограниченный прогресс.[33] Однако кажется вероятным, что основное влияние на теорию туннелирования Фаулера-Нордхейма (по сути) будет заключаться в изменении значений п и ν в экв. (15), суммами, которые в настоящее время трудно оценить.
Все эти замечания в принципе применимы к туннелированию Фаулером-Нордхеймом из любого проводника, где (до туннелирования) электроны можно рассматривать как в состояния бегущей волны. Подход может быть адаптирован для применения (приблизительно) к ситуациям, когда электроны изначально находятся в локализованные состояния на или очень близко к излучающей поверхности, но это выходит за рамки данной статьи.
Распределение общей энергии
Распределение энергии испускаемых электронов важно как для научных экспериментов, в которых распределение энергии испускаемых электронов используется для исследования характеристик излучателя. физика поверхности[34] и для источников автоэмиссии, используемых в электронно-лучевых приборах, таких как электронные микроскопы.[42] В последнем случае «ширина» (по энергии) распределения влияет на то, насколько точно может быть сфокусирован луч.
Теоретическое объяснение здесь следует подходу Forbes.[73] Если ε обозначает полная энергия электронов относительно уровня Ферми эмиттера, и Kп обозначает кинетическая энергия электрона параллельно поверхности эмиттера, то электронная нормальная энергия εп (иногда называемая «прямой энергией») определяется как
- .
Различают два типа теоретического распределения энергии: распределение нормальной энергии (NED), который показывает, как энергия εп распространяется сразу после излучения (т.е. сразу за туннельным барьером); и распределение полной энергии, который показывает, как полная энергия ε распространяется. Когда эмиттер уровень Ферми используются в качестве опорного уровня нулевого, так ε и εп может быть как положительным, так и отрицательным.
Эксперименты по энергетическому анализу полевых эмиттеров проводились с 1930-х годов. Однако только в конце 1950-х годов это было реализовано (Янг и Мюллер[31] [, YM58]), что в этих экспериментах всегда измерялось распределение полной энергии, которое теперь обычно обозначают j(ε). Это также верно (или почти верно), когда излучение исходит от небольшого выступа, усиливающего поле, на плоской поверхности.[34]
Чтобы увидеть, как можно рассчитать полное распределение энергии в рамках Модель типа свободных электронов Зоммерфельдапосмотрите на Энергетическая пространственная диаграмма P-T (P-T = «параллельное общее»).
Это показывает "параллель кинетическая энергия" Kп по горизонтальной оси и полная энергия ε по вертикальной оси. Электрон внутри объемного металла обычно имеет значения Kп и ε которые лежат в слегка заштрихованной области. Можно показать, что каждый элемент dεdKп этого энергетического пространства вносит вклад плотности электронного тока, падающего на внутреннюю границу эмиттера.[73] Здесь, zS универсальная постоянная (называемая здесь Зоммерфельд плотность предложения):
и это Функция распределения Ферми – Дирака:
куда Т является термодинамическая температура и kB является Постоянная Больцмана.
Этот элемент плотности падающего тока видит барьер высотой час предоставлено:
Соответствующие вероятность побега является D(час,F): это может быть расширено (приблизительно) в виде[73]
куда DF вероятность выхода для барьера неуменьшенной высоты, равной местная рабочая функция φ. Следовательно, элемент dεdKп вносит вклад в плотность тока эмиссии и суммарный вклад падающих электронов с энергиями в элементарном диапазоне dε таким образом
- ,
где интеграл в принципе берется вдоль полосы, показанной на диаграмме, но на практике может быть расширен до ∞, когда ширина затухания dF намного меньше, чем Энергия Ферми KF (что всегда бывает с металлом). Результат интеграции можно записать:
куда и - значения, подходящие для барьера неуменьшенной высоты час равна локальной работе выхода φ, и определяется этим уравнением.
Для данного эмиттера с заданным полем, приложенным к нему, не зависит от F, так ур. (21) показывает, что форма распределения (как ε возрастает от отрицательного значения значительно ниже уровня Ферми) - возрастающая экспонента, умноженная на Функция распределения ФД. Это генерирует знакомую форму распределения, впервые предсказанную Янгом.[31] При низких температурах резко идет от 1 до 0 в окрестности уровня Ферми, а FWHM распределения определяется:
Тот факт, что экспериментальные распределения полной энергии CFE имеют эту базовую форму, является хорошим экспериментальным подтверждением того, что электроны в металлах подчиняются Статистика Ферми – Дирака.
Электронная эмиссия холодного поля
Уравнения типа Фаулера – Нордхейма
Вступление
Уравнения типа Фаулера – Нордхейма в J-F форме, являются (приближенными) теоретическими уравнениями, выведенными для описания локальной плотности тока J испускается из внутренних электронных состояний в зона проводимости из наливного металла. В плотность тока эмиссии (ECD) J для некоторой малой однородной области излучающей поверхности обычно выражается как функция J(φ,F) из местная рабочая функция φ и локальное барьерное поле F которые характеризуют небольшой регион. Для резко изогнутых поверхностей J может также зависеть от параметра (ов), используемых для описания кривизны поверхности.
Благодаря физическим предположениям, сделанным в исходном выводе,[1] период, термин Уравнение типа Фаулера-Нордхейма долгое время использовался только для уравнений, описывающих ЭЦП при нулевой температуре. Однако лучше позволить этому названию включать слегка измененные уравнения (обсуждаемые ниже), которые действительны для конечных температур в режиме эмиссии CFE.
Форма с нулевой температурой
Плотность тока лучше всего измерять в А / м.2. Полная плотность тока, излучаемого из небольшой однородной области, может быть получена путем интегрирования полного распределения энергии j(ε) по полной энергии электронов ε. При нулевой температуре Функция распределения Ферми – Дирака жFD = 1 для ε<0 и жFD = 0 для ε> 0. Таким образом, ECD при 0 K, J0, дается из ур. (18) автор:
куда это эффективное предложение для государства F, и определяется этим уравнением. Строго, нижний предел интеграла должен быть -KF, куда KF это Энергия Ферми; но если dF намного меньше, чем KF (что всегда имеет место для металла), то значительного вклада в интеграл не дают энергии ниже KF, и формально его можно продолжить до –∞.
Результату (23) можно дать простую и полезную физическую интерпретацию, обратившись к рис. 1. Электронное состояние в точке «F» на диаграмме («состояние F») является «движущимся вперед состоянием на уровне Ферми» (т. Е. , он описывает электрон уровня Ферми, движущийся по нормали к поверхности эмиттера и по направлению к ней). При 0 К электрон в этом состоянии видит барьер нередуцированной высоты φ, и имеет вероятность выхода DF что выше, чем для любого другого занятого электронного состояния. Так удобно писать J0 в качестве ZFDF, где «эффективное предложение» ZF - плотность тока, которая должна была бы быть перенесена состоянием F внутри металла, если бы вся эмиссия вышла из состояния F.
На практике плотность тока в основном возникает из группы состояний, близких по энергии к состоянию F, большая часть которых находится внутри сильно заштрихованной области на диаграмме энергетического пространства. Поскольку для модель свободных электронов, вклад в плотность тока прямо пропорционален площади в энергетическом пространстве (с Зоммерфельд плотность предложения zS как константа пропорциональности), полезно думать о ECD как о взятом из электронных состояний в области размером dF2 (измеряется в эВ2) на диаграмме энергия-пространство. То есть, полезно думать о ECD, как о взятом из состояний в сильно заштрихованной области на рис. 1. (Это приближение медленно ухудшается с повышением температуры).
ZF также можно записать в виде:
где универсальная постоянная а, иногда называемый Первая константа Фаулера – Нордхейма, дан кем-то
Это ясно показывает, что предэкспоненциальный множитель а φ−1F2, которая появляется в уравнениях типа Фаулера-Нордхейма, связана с эффективным подводом электронов к поверхности эмиттера в модели свободных электронов.
Ненулевые температуры
Чтобы получить результат, действительный для ненулевой температуры, отметим из ур. (23) что zSdFDF = J0/dF. Итак, когда эк. (21) интегрируется при ненулевой температуре, затем - после такой замены и вставки явного вида Функция распределения Ферми – Дирака - ECD J можно записать в виде:
куда λТ - коэффициент температурной поправки, определяемый интегралом. Интеграл можно преобразовать, написав и , а потом , в стандартный результат:[74]
Это действительно для ш> 1 (т.е. dF/kBТ > 1). Следовательно - для таких температур, что kBТ<dF:
где разложение справедливо, только если (πkBТ /dF) << 1. Пример значения (для φ= 4,5 эВ, F= 5 В / нм, Т= 300 К) составляет λТ= 1,024. Нормальное мышление заключалось в том, что в режиме ДОВСЕ λТ всегда мала по сравнению с другими неопределенностями, и что обычно нет необходимости явно включать его в формулы для плотности тока при комнатной температуре.
Режимы излучения металлов на практике определяются диапазонами барьерного поля F и температура Т для которого математически адекватно данное семейство уравнений излучения. Когда барьерное поле F достаточно высока для работы режима CFE для эмиссии металла при 0 K, то условие kBТ<dF дает формальную верхнюю границу (по температуре) режима эмиссии CFE. Однако утверждалось, что (из-за приближений, сделанных где-либо в выводе) условие kBТ<0.7dF - лучший рабочий предел: это соответствует λТ-значение около 1,09, и (для примера) верхний предел температуры в режиме CFE около 1770 К. Этот предел является функцией поля барьера.[33][72]
Отметим, что результат (28) здесь применим для барьера любой формы (хотя dF будет разным для разных барьеров).
Физически полное уравнение типа Фаулера – Нордхейма
Результат (23) также приводит к некоторому пониманию того, что происходит при учете эффектов атомного уровня и ленточная структура больше не похож на свободный электрон. Благодаря наличию атомных ионных остовов, поверхностного барьера, а также электронного волновые функции на поверхности будет иначе. Это повлияет на значения поправочного коэффициента. , префактор п, и (в ограниченной степени) поправочный коэффициент λd. Эти изменения, в свою очередь, повлияют на значения параметра DF и (в ограниченной степени) параметр dF. Для настоящего металла плотность подачи будет меняться в зависимости от положения в энергетическом пространстве, а значение в точке «F» может отличаться от плотности подачи по Зоммерфельду. Мы можем учесть этот эффект, введя поправочный коэффициент для электронной зонной структуры λB в ур. (23). Модинос обсуждал, как можно рассчитать этот коэффициент: он оценивает, что он, скорее всего, находится между 0,1 и 1; он может лежать за этими пределами, но маловероятно, что он выйдет за пределы диапазона 0,01 <λB<10.[75]
Путем определения общего поправочного коэффициента предложения λZ равно λТ λB λd2, и комбинируя приведенные выше уравнения, мы получаем так называемое физически полное уравнение типа Фаулера-Нордхейма:[76]
куда [=(φ,F)] - коэффициент поправки на показатель степени для барьера неуменьшенной высоты. φ. Это наиболее общее уравнение типа Фаулера – Нордгейма. Другие уравнения в семействе получаются путем подстановки конкретных выражений для трех поправочных коэффициентов , пF и λZ это содержит. Так называемое элементарное уравнение типа Фаулера-Нордхейма, которое появляется в школьных учебниках по полевой эмиссии, получается, если положить λZ→1, пF→1, → 1; это не дает хороших количественных предсказаний, потому что делает барьер сильнее, чем он есть в физической реальности. Так называемое стандартное уравнение типа Фаулера-Нордхейма, первоначально разработанное Мерфи и Гудом,[72] и часто используется в прошлой литературе, получается, если положить λZ→тF−2, пF→1, →vF, куда vF является v(ж), куда ж это ценность жчас полученный путем помещения час=φ, и тF - связанный параметр (близкий к единице).[69]
В рамках более полной теории, описанной здесь, фактор тF−2 является составной частью поправочного коэффициента λd2 [видеть,[67] и обратите внимание, что λd2 обозначается λD там]. Нет особой ценности в продолжении отдельной идентификации тF−2. Вероятно, при нынешнем уровне знаний наилучшее приближение для моделирования CFE из металлов на основе простого уравнения Фаулера-Нордхейма получается, если положить λZ→1, пF → 1, → v(ж). Это воссоздает уравнение типа Фаулера-Нордхейма, использованное Дайком и Доланом в 1956 году, и может быть названо «упрощенным стандартным уравнением типа Фаулера-Нордхейма».
Рекомендуемая форма для простых вычислений типа Фаулера – Нордхейма
Ясно, что это рекомендуется упрощенное стандартное уравнение типа Фаулера-Нордхейма, и соответствующие формулы:
куда Fφ вот поле, необходимое для сведения к нулю барьера Шоттки-Нордхейма нередуцированной высоты, равной местная рабочая функция φ, и ж - масштабируемое барьерное поле для барьера Шоттки-Нордхейма неуменьшенной высоты φ. [Это количество ж можно было бы написать более точно как жφSN, но это делает это уравнение типа Фаулера-Нордхайма менее загроможденным, если принять такое простое соглашение. ж означает величину, обозначенную жφSN в,[69] экв. (2.16).] Для примера (φ= 4,5 эВ, F= 5 В / нм), ж≈ 0,36 и v(ж) ≈ 0,58; практические диапазоны этих параметров обсуждаются далее в.[77]
Обратите внимание, что переменная ж (масштабируемое поле барьера) не то же самое, что переменная у (параметр Нордхейма) широко использовался в прошлой литературе по полевой эмиссии, и что " v(ж) "НЕ имеет того же математического значения и значений, что и количество" v(у) ", которая появляется в литературе по автоэмиссии. В контексте описанной здесь пересмотренной теории формулы для v(у), и таблицы значений для v(у) следует игнорировать или рассматривать как значения v(ж1/2). Если более точные значения для v(ж) требуются, то[69] предоставляет формулы, которые дают значения для v(ж) с абсолютной математической точностью лучше 8 × 10−10. Однако приведенная выше аппроксимационная формула (30c), которая дает значения с точностью до абсолютной математической точности лучше 0,0025, должна давать значения, достаточно точные для всех технологических целей.[69]
Комментарии
Необходима историческая справка о методах вывода уравнений типа Фаулера-Нордхейма. Есть несколько возможных подходов к выводу этих уравнений с использованием теория свободных электронов. Используемый здесь подход был введен Forbes в 2004 году и может быть описан как «интегрирование через распределение полной энергии с использованием параллельной кинетической энергии. Kп как первая переменная интегрирования ».[73] По сути, это эквивалент процедуры Модиноса для свободных электронов.[33][75] (в более продвинутой квантово-механической трактовке) «интегрирования по поверхности зоны Бриллюэна». Напротив, трактовка CFE Янга в 1959 г.[31] Гадзук и Пламмер в 1973 году[34] и Модинос в 1984 г.,[33] также интегрировать через общее распределение энергии, но использовать нормальную энергию εп (или связанная величина) в качестве первой переменной интегрирования.
Существует также более старый подход, основанный на основополагающей статье Нордхайма в 1928 г.[78] который формулирует проблему иначе, а затем использует сначала Kп а потом εп (или связанная величина) в качестве переменных интегрирования: это известно как «интегрирование через распределение нормальной энергии». Некоторые авторы продолжают использовать этот подход. Хотя он имеет некоторые преимущества, особенно при обсуждении резонансных явлений, он требует интегрирования функции распределения Ферми-Дирака на первом этапе интегрирования: для электронных зонных структур, подобных свободным электронам, это может привести к очень сложным и ошибочным результатам. склонная математика (как в работе Стрэттона по полупроводники).[79] Кроме того, интегрирование через распределение нормальной энергии не дает экспериментально измеренных распределений энергии электронов.
В целом, используемый здесь подход кажется более легким для понимания и приводит к более простой математике.
Он также в принципе ближе к более сложным подходам, используемым при работе с реальными объемными кристаллическими твердыми телами, где первым шагом является либо интегрирование вкладов в ECD по поверхности постоянной энергии в волновой вектор Космос ( k -Космос),[34] или интегрировать вклады по соответствующей зоне Бриллюэна на поверхности.[33] Подход Форбса эквивалентен интегрированию по сферической поверхности в k-space, используя переменную Kп для определения кольцевого интегрирующего элемента, имеющего цилиндрическую симметрию относительно оси в направлении, нормальном к излучающей поверхности, или для интегрирования по (протяженной) поверхности зоны Бриллюэна с использованием круговых кольцевых элементов.
Теоретические уравнения CFE
В предыдущем разделе объясняется, как выводить уравнения типа Фаулера-Нордхейма. Строго говоря, эти уравнения применимы только к CFE из массивных металлов. Идеи, изложенные в следующих разделах, применимы к ДОВСЕ в более общем плане, но ур. (30) будет использоваться для их иллюстрации.
Для CFE базовые теоретические трактовки обеспечивают связь между локальной плотностью тока эмиссии. J и локальное барьерное поле F, в локальном положении на излучающей поверхности. Эксперименты измеряют ток эмиссии я от некоторой определенной части эмиссионной поверхности в зависимости от напряжения V применяется к некоторому противоэлектроду. Чтобы связать эти переменные с J и F, используются вспомогательные уравнения.
В коэффициент преобразования напряжения в барьерное поле β определяется:
Значение F изменяется от позиции к позиции на поверхности эмиттера, а значение β соответственно меняется.
Для металлического эмиттера β- значение для данного положения будет постоянным (независимо от напряжения) при следующих условиях: (1) устройство представляет собой «диодную» схему, в которой присутствуют только электроды, являющиеся эмиттером и набором «окружения», все части которые находятся под одинаковым напряжением; (2) отсутствие значительного полевого вакуума объемный заряд (FEVSC) присутствует (это будет верно, за исключением очень высоких плотностей эмиссионного тока, около 109 Являюсь2 или выше[27][80]); (3) не существует значимых «полей патча»,[63] в результате неоднородности местная рабочая функция (обычно предполагается, что это правда, но может быть не в некоторых обстоятельствах). Для неметаллов физические эффекты, называемые «проникновение поля» и «изгиб ленты"[M084] может сделать β функция приложенного напряжения, хотя, что удивительно, исследований этого эффекта мало.
Плотность тока эмиссии J меняется от позиции к позиции по поверхности эмиттера. Полный ток эмиссии я из определенной части эмиттера получается интегрированием J через эту часть. Чтобы получить простое уравнение для я(V) используется следующая процедура. Контрольная точка "r" выбирается в этой части поверхности эмиттера (часто точка, в которой плотность тока самая высокая), и плотность тока в этой контрольной точке обозначается как Jр. Параметр Ар, называется условная площадь выброса (относительно точки "r") определяется следующим образом:
где интеграл берется по интересующей части эмиттера.
Этот параметр Ар была введена в теорию CFE Стерном, Госслингом и Фаулером в 1929 г. (которые назвали ее «средневзвешенной площадью»).[16] Для практических излучателей плотность тока эмиссии, используемая в уравнениях типа Фаулера-Нордхейма, всегда является плотностью тока в некоторой контрольной точке (хотя это обычно не указывается). Давно установленное соглашение обозначает эту эталонную плотность тока простым символом J, а соответствующее локальное поле и коэффициент преобразования простыми символами F и βбез индекса "r", использованного выше; в дальнейшем используется это соглашение.
Условная площадь выброса Ар часто будет функция локального поля отсчета (и, следовательно, напряжение),[30] а в некоторых случаях это может быть значительная функция температуры.
Потому что Ар имеет математическое определение, оно не обязательно соответствует области, из которой наблюдается излучение от одноточечного излучателя в полевой электронный (эмиссионный) микроскоп. С эмиттером большой площади, который содержит множество отдельных участков излучения, Ар почти всегда будет очень очень[требуется разъяснение] намного меньше, чем «макроскопическая» геометрическая площадь (АM) излучателя при визуальном наблюдении (см. ниже).
Включая эти вспомогательные уравнения в ур. (30a) дает
Это упрощенное стандартное уравнение типа Фаулера-Нордхейма в я-V форма. Соответствующее «физически полное» уравнение получается умножением на λZпF.
Модифицированные уравнения для излучателей большой площади
Уравнения в предыдущем разделе применимы ко всем полевым эмиттерам, работающим в режиме CFE. Однако дальнейшие разработки полезны для излучателей с большой площадью, которые содержат много отдельных участков выбросов.
Для таких излучателей условная площадь выброса почти всегда будет очень высокой.[требуется разъяснение] намного меньше, чем кажущаяся "макроскопическая" геометрическая площадь (АM) физического излучателя, наблюдаемого визуально. Безразмерный параметр αр, площадь эффективности излучения, можно определить как
Кроме того, «макроскопическая» (или «средняя») плотность тока эмиссии JM (усредненное по геометрической площади АM эмиттера) можно определить и связать с эталонной плотностью тока Jр использованный выше
Это приводит к следующим "версиям для больших площадей" упрощенного стандартного уравнения типа Фаулера-Нордхейма:
Оба эти уравнения содержат площадную эффективность выбросов αр. Для любого данного эмиттера этот параметр имеет значение, которое обычно малоизвестно. В целом, αр сильно различается как между разными материалами излучателя, так и между разными образцами одного и того же материала, приготовленными и обработанными по-разному. Значения в диапазоне 10−10 до 10−6 кажутся вероятными, и значения вне этого диапазона могут быть возможны.
Наличие αр в экв. (36) учитывает разницу между макроскопическими плотностями тока, часто цитируемыми в литературе (обычно 10 А / м2 для многих видов излучателей большой площади, кроме Массивы шпиндта[50]) и местные плотности тока в местах фактического выброса, которые могут варьироваться в широких пределах, но которые, как считается, обычно составляют порядка 109 Являюсь2или, возможно, чуть меньше.
В значительной части технической литературы по эмиттерам большой площади не проводится четких различий между локальной и макроскопической плотностями тока или между условной площадью излучения. Ар и макроскопическая область АM, и / или опускает параметр αр из процитированных уравнений. Необходима осторожность, чтобы избежать ошибок интерпретации.
Иногда бывает удобно разделить коэффициент преобразования βр на «макроскопическую часть», которая относится к общей геометрии излучателя и его окружения, и «локальную часть», которая относится к способности очень локальной структуры поверхности излучателя усиливать электрическое поле. Обычно это делается путем определения «макроскопического поля». FM это поле, которое будет присутствовать в месте излучения в отсутствие локальной структуры, вызывающей усиление. Это поле FM связан с приложенным напряжением «коэффициентом преобразования напряжения в макроскопическое поле» βM определяется:
В общем случае системы, состоящей из двух параллельных пластин, разделенных расстоянием W, на одной из которых созданы излучающие наноструктуры, βM = 1/W.
«Фактор усиления поля» γ затем определяется и соотносится со значениями βр и βM к
С эк. (31), это дает следующие формулы:
где, в соответствии с обычным соглашением, суффикс «r» теперь удален из параметров, относящихся к контрольной точке. Существуют формулы для оценки γ, с помощью классическая электростатика, для самых разных форм излучателей, в частности «полусфера на столбе».[81]
Уравнение (40) означает, что версии уравнений типа Фаулера-Нордхейма могут быть записаны где либо F или же βV везде заменяется на . Это часто делается в технологических приложениях, где основной интерес представляют улучшающие поле свойства наноструктуры с локальным эмиттером. Однако в некоторых прошлых работах не удалось провести четкое различие между барьерным полем. F и макроскопическое поле FM вызвал путаницу или ошибку.
В более общем плане, цели технологического развития полевых эмиттеров большой площади состоят в том, чтобы повысить однородность излучения за счет увеличения значения площади эффективности излучения. αр, и уменьшить "начальное" напряжение, при котором возникает значительная эмиссия, путем увеличения значения β. Уравнение (41) показывает, что это можно сделать двумя способами: либо пытаясь развить «высокоэффективный»γ"наноструктуры, или путем изменения общей геометрии системы так, чтобы βM увеличена. Существуют различные компромиссы и ограничения.
На практике, хотя определение макроскопического поля, используемое выше, является наиболее распространенным, в литературе используются другие (по-разному определенные) типы макроскопического поля и коэффициента усиления поля, особенно в связи с использованием зондов для исследования я-V характеристики отдельных излучателей.[82]
В технологическом контексте данные о полевых выбросах часто строятся с использованием (конкретного определения) FM или 1 /FM как Икс-координат. Однако для научного анализа обычно лучше не предварительно манипулировать экспериментальными данными, а строить необработанные измеренные данные. я-V данные напрямую. Значения технологических параметров, таких как (различные формы) γ затем можно получить из подобранных параметров я-V график данных (см. ниже) с использованием соответствующих определений.
Модифицированные уравнения для нанометрически острых эмиттеров
Большинство теоретических выводов в теории автоэмиссии сделано в предположении, что барьер принимает форму Шоттки-Нордхейма ур. (3). Однако такая форма барьера не подходит для излучателей с радиусами кривизны. сравнима с длиной туннельного барьера. Последнее зависит от работы выхода и поля, но в случаях, представляющих практический интерес, приближение SN-барьера можно считать справедливым для излучателей с радиусами , как объяснено в следующем абзаце.
Основное предположение приближения барьера SN состоит в том, что член электростатического потенциала принимает линейный вид в районе проходки туннелей. Последнее было доказано, только если .[83] Следовательно, если область туннелирования имеет длину , для всех что определяет процесс туннелирования; таким образом, если экв. (1) выполняется и приближение SN-барьера справедливо. Если вероятность туннелирования достаточно высока для получения измеримой полевой эмиссии, L не превышает 1-2 нм. Следовательно, барьер SN справедлив для излучателей с радиусами порядка нескольких десятков нм.
Однако современные излучатели намного острее этого, с радиусом порядка нескольких нм. Следовательно, стандартное уравнение FN или любая его версия, предполагающая барьер SN, приводит к значительным ошибкам для таких резких излучателей. Это было показано теоретически.[84][85] и подтверждено экспериментально.[86]
Вышеупомянутая проблема была рассмотрена в исх.[83] Барьер SN был обобщен с учетом кривизны излучателя. Можно доказать, что электростатический потенциал вблизи любой металлической поверхности с радиусом кривизны возможно асимптотически расширенный в качестве
Кроме того, потенциал изображения для резкого излучателя лучше представлен тем, который соответствует сферической металлической поверхности, а не плоской. Пренебрегая всем В терминах общий потенциальный барьер принимает форму, найденную Кирицакисом и Ксантакисом[83]
Если Приближение JWKB (4) используется для этого барьера, показатель Гамова принимает форму, которая обобщает уравнение. (5)
куда определяется формулой (30d), дается формулой (30c) и - это новая функция, которая может быть аппроксимирована аналогично (30c) (в ссылке есть типографические ошибки,[83] исправлено здесь):
Учитывая выражение для показателя Гамова как функции высоты бесполевого барьера , излучаемая плотность тока для холодной автоэлектронной эмиссии может быть получена из уравнения. (23). Это дает
где функции и определяются как
и
В уравнении (46) для полноты картины не аппроксимируется единицей, как в (29) и (30a), хотя для большинства практических случаев это очень хорошее приближение. Помимо этого, уравнения (43), (44) и (46) совпадают с соответствующими уравнениями стандартная теория Фаулера-Нордгейма (3), (9), (30a) в пределе ; это ожидаемо, поскольку первые уравнения обобщают последние.
Наконец, отметим, что приведенный выше анализ является асимптотическим в пределе , аналогично стандартной теории Фаулера-Нордхейма с использованием барьера сверхновой. Однако добавление квадратичных членов делает его значительно более точным для излучателей с радиусом кривизны в диапазоне ~ 5-20 нм. Для более острых эмиттеров нет общего приближения для плотности тока. Чтобы получить плотность тока, необходимо вычислить электростатический потенциал и оценить JWKB интеграл численно. Для этого разработаны научные вычислительные программные библиотеки.[87]
Эмпирический CFE я–V уравнение
На современном этапе развития теории CFE важно проводить различие между теоретическими уравнениями CFE и эмпирическими уравнениями CFE. Первые заимствованы из физики конденсированного состояния (хотя и в контекстах, где их детальное развитие затруднительно). С другой стороны, эмпирическое уравнение CFE просто пытается представить фактическую экспериментальную форму зависимости тока я по напряжению V.
В 1920-х годах эмпирические уравнения использовались, чтобы найти мощность V который появился в показателе степени полулогарифмического уравнения, которое, как предполагается, описывает экспериментальные результаты CFE. В 1928 году теория и эксперимент были объединены, чтобы показать, что (за исключением, возможно, очень острых излучателей) эта мощность V−1. Недавно было предложено провести эксперименты CFE, чтобы попытаться найти мощность (κ) из V в предэкспоненте следующего эмпирического уравнения CFE:[88]
куда B, C и κ рассматриваются как константы.
Из ур. (42) легко показать, что
В 1920-х годах экспериментальные методы не могли различить результаты κ = 0 (предположили Милликен и Лортисен).[13] и κ = 2 (предсказано исходным уравнением типа Фаулера-Нордхейма).[1] Однако теперь должно быть возможно проводить достаточно точные измерения dlni / d (1 / V) (при необходимости, используя синхронный усилитель/ фазочувствительные методы обнаружения и оборудование с компьютерным управлением), а также для получения κ от наклона соответствующего графика данных.[50]
После открытия приближения (30b) теперь очень ясно, что даже для CFE из массивных металлов значение κ= 2 не ожидается. Это можно показать следующим образом. Используя ур. (30c) выше безразмерный параметр η может быть определено
За φ = 4,50 эВ, этот параметр имеет значение η = 4,64. С ж = F/Fφ и v(ж) дается уравнением (30b), показатель степени в упрощенном стандартном уравнении типа Фаулера-Нордхейма (30) можно записать в альтернативной форме и затем развернуть следующим образом:[69]
При условии, что коэффициент пересчета β не зависит от напряжения, параметр ж имеет альтернативное определение ж = V/Vφ, куда Vφ напряжение, необходимое в конкретной экспериментальной системе, чтобы уменьшить высоту барьера Шоттки-Нордхейма с φ до нуля. Таким образом, ясно, что фактор v(ж) в показатель степени теоретического уравнения (30) приводит к дополнительным V-зависимость в предэкспоненциальный эмпирического уравнения. Таким образом, (для эффектов, связанных с барьером Шоттки-Нордхейма, и для эмиттера с φ= 4,5 эВ) получаем прогноз:
Поскольку в уравнении типа Фаулера-Нордхейма также может быть зависимость от напряжения в других факторах, в частности, в условной зоне выбросов[30] Ар и в локальной работе выхода не обязательно ожидать, что κ для ДФЭ из металла с локальной работой выхода 4,5 эВ должно иметь значение κ = 1,23, но, конечно, нет оснований ожидать, что оно будет иметь исходное значение Фаулера-Нордхейма κ = 2.[89]
Первая экспериментальная проверка этого предложения была проведена Кирком, который использовал несколько более сложную форму анализа данных, чтобы найти значение 1,36 для своего параметра. κ. Его параметр κ очень похож, но не то же самое, что параметр κ используется здесь, но тем не менее его результаты, кажется, подтверждают потенциальную полезность этой формы анализа.[90]
Использование эмпирического уравнения CFE (42) и измерение κ, может быть особенно полезен для неметаллов. Строго говоря, уравнения типа Фаулера-Нордхейма применимы только к излучению из зона проводимости навалом кристаллический твердые тела. Однако эмпирические уравнения вида (42) должны применяться ко всем материалам (хотя, вероятно, для очень острых излучателей может потребоваться модификация). Кажется весьма вероятным, что одно из отличий уравнений CFE для новых материалов от уравнений типа Фаулера-Нордхейма состоит в том, что эти уравнения CFE могут иметь различную степень F (или же V) в их предэкспонентах. Измерения κ может служить некоторым экспериментальным указанием на это.
Графики Фаулера – Нордхейма и Милликена – Лауритсена
Исходное теоретическое уравнение, полученное Фаулером и Нордхеймом[1] за последние 80 лет повлиял на способ построения и анализа экспериментальных данных CFE. В очень широко используемом графике Фаулера-Нордхейма, представленном Штерном и другие. в 1929 г.,[16] количество ln {я/V2} строится против 1 /V. Первоначальное мышление заключалось в том, что (как предсказывалось исходным или элементарным уравнением типа Фаулера-Нордхейма) это создаст точную прямую линию наклона SFN. SFN будут связаны с параметрами, которые входят в показатель степени уравнения типа Фаулера-Нордхейма я-V форма:
Следовательно, знание φ разрешит β подлежат определению, или наоборот.
[В принципе, в геометриях системы, где присутствует локальная усиливающая поле наноструктура, и коэффициент макроскопического преобразования βM можно определить, знание β затем позволяет значение эффективного коэффициента усиления поля излучателя γ определяется по формуле γ = β/βM. В обычном случае пленочного излучателя, сформированного на одной пластине двухпластинчатой конструкции с разделением пластин W (так βM = 1/W) тогда
В настоящее время это одно из наиболее вероятных применений графиков Фаулера-Нордхейма.]
Впоследствии стало ясно, что исходное мышление, приведенное выше, строго верно только для физически нереалистичной ситуации с плоским излучателем и точным треугольным барьером. Для реальных излучателей и реальных барьеров "коэффициент поправки на наклон" σFN должен быть введен, давая пересмотренную формулу
Значение σFN будет, в принципе, зависеть от любого параметра в физически полном уравнении типа Фаулера-Нордхейма для я(V), имеющий зависимость от напряжения.
В настоящее время единственным параметром, который считается важным, является поправочный коэффициент. относящийся к форме барьера, и единственный барьер, для которого существует какая-либо хорошо обоснованная подробная теория, - это барьер Шоттки-Нордхейма. В этом случае, σFN задается математической функцией, называемой s. Эта функция s была сначала правильно табулирована (как функция параметра Нордхейма у) по Берджессу, Кремер и Хьюстон в 1953 году;[71] и современное лечение, которое дает s как функция масштабированного барьерного поля ж для барьера Шоттки-Нордхейма приведен в.[69] Однако уже давно было ясно, что для практической работы эмиттера значение s лежит в диапазоне от 0,9 до 1.
На практике из-за дополнительной сложности, связанной с подробным учетом поправочного коэффициента наклона, многие авторы (фактически) полагают σFN = 1 в ур. (49), тем самым создавая систематическую ошибку в их оценочных значениях β и / или γ, обычно считалось около 5%.
Однако эмпирическое уравнение (42), которое в принципе является более общим, чем уравнения типа Фаулера-Нордхейма, дает возможные новые способы анализа полевой эмиссии. я-V данные. В целом можно предположить, что параметр B в эмпирическом уравнении связана с неприведенной высотой ЧАС некоторого характерного барьера, видимого туннелирующими электронами
(В большинстве случаев, но не обязательно во всех, ЧАС будет равняться локальной работе выхода; конечно, это верно для металлов.) Вопрос в том, как определить стоимость B экспериментально. Есть два очевидных пути. (1) Предположим, что ур. (43) можно использовать для определения достаточно точного экспериментального значения κ, от наклона графика формы [–dln {я} / d (1 /V) против. V]. В этом случае второй график ln (я)/Vκ против 1 /V, должна быть точная прямая линия наклона -B. Такой подход должен быть наиболее точным способом определения B.
(2) В качестве альтернативы, если значение κ точно не известно и не может быть точно измерено, но может быть оценено или угадано, тогда значение для B может быть получен из графика вида [ln {я} vs. 1 /V]. Это форма графика, использованная Милликеном и Лауритсеном в 1928 году. (43) дает
Таким образом, B может быть определена с хорошей степенью приближения путем определения среднего наклона графика Милликена-Лауритсена в некотором диапазоне значений 1 /V, и применив поправку, используя значение 1 /V в середине диапазона и предполагаемое значение κ.
Основные преимущества использования графика Милликена-Лауритсена и этой формы процедуры коррекции, а не графика Фаулера-Нордхейма и поправочного коэффициента наклона, заключаются в следующем. (1) Процедура построения несколько более проста. (2) Поправка включает физический параметр (V), которая является измеряемой величиной, а не физическим параметром (ж), который необходимо рассчитать [, чтобы затем вычислить значение s(ж) или, в более общем смысле σFN(ж)]. (3) Оба параметра κ сам по себе и процедура исправления более прозрачны (и легче понимаются), чем эквиваленты графика Фаулера-Нордхейма. (4) Эта процедура учитывает все физические эффекты, влияющие на величину κ, в то время как процедура коррекции графика Фаулера-Нордхейма (в той форме, в которой она проводилась в течение последних 50 лет) учитывает только те эффекты, которые связаны с формой барьера - при условии, кроме того, что эта форма является формой Шоттки. -Барьер Нордхейма. (5) Существует более четкое разделение теоретических и технологических проблем: теоретики будут заинтересованы в установлении, какой информации какие-либо измеренные значения κ рассказать о теории ДОВСЕ; но экспериментаторы могут просто использовать измеренные значения κ для получения более точных оценок (при необходимости) коэффициентов усиления месторождения.[нужна цитата]
Эту процедуру коррекции для графиков Милликена-Лауритсена станет проще применять, когда будет проведено достаточное количество измерений κ были сделаны, и есть лучшее представление о типичных значениях на самом деле. В настоящее время кажется вероятным, что для большинства материалов κ будет лежать в диапазоне -1 <κ<3.[нужна цитата]
Дополнительная теоретическая информация
Разработать приближенную теорию CFE из металлов, описанных выше, сравнительно легко по следующим причинам. (1) Теория свободных электронов Зоммерфельда, с его частными предположениями о распределении внутренних электронных состояний по энергиям, в первом приближении адекватно применима ко многим металлам. (2) В большинстве случаев металлы не имеют поверхностные состояния и (во многих случаях) металл волновые функции не имеют значительного "поверхностные резонансы". (3) Металлы имеют высокую плотность состояний на уровне Ферми, поэтому заряд, который генерирует / экранирует внешние электрические поля, лежит в основном за пределами верхнего атомного слоя, и никакого значимого «проникновения поля» не происходит. (4) Металлы имеют высокий электрическая проводимость: внутри металлических эмиттеров не происходит значительных падений напряжения: это означает, что нет факторов, препятствующих подаче электронов к эмиттирующей поверхности, и что электроны в этой области могут находиться как в эффективных локальных термодинамическое равновесие и в эффективном термодинамическом равновесии с электронами в опорной конструкции металла, на которых установлен излучатель. (5) Эффекты атомарного уровня не принимаются во внимание.[нужна цитата]
Развитие «простых» теорий автоэлектронной эмиссии и, в частности, разработка уравнений типа Фаулера-Нордхейма, опирается на истинность всех пяти из вышеперечисленных факторов. Для материалов, отличных от металлов (и для металлических эмиттеров с атомарной остротой), один или несколько из вышеперечисленных факторов будут неверными. Например, кристаллический полупроводники не имеют зонной структуры, подобной свободным электронам, имеют поверхностные состояния, подвержены проникновению поля и изгиб ленты, и может демонстрировать как внутренние падения напряжения, так и статистическую развязку распределения электронов в поверхностных состояниях от распределения электронов в приповерхностной области объема ленточная структура (такое разделение известно как «эффект Модиноса»).[33][91]
На практике теория фактического туннельного процесса Фаулера-Нордхейма во многом одинакова для всех материалов (хотя детали формы барьера могут различаться, и модифицированная теория должна быть разработана для начальных состояний, которые являются локализованными, а не являются бегущая волна). Однако, несмотря на такие различия, можно ожидать (для термодинамическое равновесие ситуаций), что все уравнения CFE будут иметь показатели, которые в целом ведут себя одинаково. Вот почему применение уравнений типа Фаулера-Нордхейма к материалам, выходящим за рамки приведенных здесь выводов, часто работает. Если интерес представляют только параметры (такие как коэффициент усиления поля), которые относятся к наклону графиков Фаулера-Нордхейма или Милликена-Лауритсена и к показателю степени уравнения CFE, то теория типа Фаулера-Нордхейма часто дает разумные оценки. Однако попытки получить значимые значения плотности тока обычно или всегда терпят неудачу.
Обратите внимание, что прямая линия на графике Фаулера-Нордхейма или Милликена-Лауритсена нет указывают на то, что излучение из соответствующего материала подчиняется уравнению типа Фаулера-Нордхейма: это указывает только на то, что механизм излучения отдельных электронов, вероятно, является туннелированием Фаулера-Нордхейма.[нужна цитата]
Различные материалы могут иметь радикально разные распределения по энергиям своих внутренних электронных состояний, поэтому процесс интегрирования вкладов плотности тока по внутренним электронным состояниям может привести к существенно разным выражениям для предэкспонент плотности тока для разных классов материалов. . В частности, мощность барьерного поля в предэкспоненте может отличаться от исходного значения Фаулера-Нордхейма «2». Исследование эффектов такого рода - активная тема для исследований. "Резонанс" и "на атомном уровне"рассеяние«эффекты, если они возникнут, также изменят теорию.
Если материалы подвержены проникновению в поле и изгибу ленты, необходимо иметь хорошие теории таких эффектов (для каждого отдельного класса материалов), прежде чем можно будет разработать детальные теории CFE. Когда возникают эффекты падения напряжения, теория эмиссионного тока может в большей или меньшей степени стать теорией, которая включает в себя эффекты внутреннего переноса, и может стать очень сложной.
Смотрите также
- Автоэмиссионный микроскоп
- Автоэмиссионные зонды
- Массив полевого эмиттера
- Индикация автоэмиссии
- Эффект Франца – Келдыша.
Рекомендации
- ^ а б c d е ж Fowler, R.H .; Доктор Л. Нордхейм (1928-05-01). «Электронная эмиссия в интенсивных электрических полях» (PDF). Труды Королевского общества А. 119 (781): 173–181. Bibcode:1928RSPSA.119..173F. Дои:10.1098 / rspa.1928.0091. Получено 2009-10-26.
- ^ Винклер, Дж. (1744 г.). Gedanken von den Eigenschaften, Wirkungen und Ursachen der Electricität nebst Beschreibung zweiner electrischer Maschinen. Лейпциг: Книжная глава Брайткопфа.
- ^ Томсон, Дж. Дж. (Октябрь 1897 г.). «Катодные лучи». Фил. Mag. 5-я серия. 44 (269): 293–316. Дои:10.1080/14786449708621070.
- ^ Ричардсон, О. (1916). Эмиссия электричества горячими телами. Лондон: Лонгманс.
- ^ Эйнштейн, А. (1905). «Об эвристической точке зрения на создание и преобразование света». Анна. Phys. Chem. 17 (6): 132–148. Bibcode:1905AnP ... 322..132E. Дои:10.1002 / andp.19053220607.
- ^ а б Ричардсон, О. (1929). «Термоэлектронные явления и законы, которые ими управляют» (PDF). Нобелевские лекции по физике 1922-1941 гг.. Получено 2009-10-25.
- ^ а б c Лилиенфельд, Дж. Э. (1922). Являюсь. J. Рентгенол. 9: 192. Отсутствует или пусто
| название =(помощь) - ^ Кляйнт, К. (1993). «О ранней истории автоэлектронной эмиссии, включая попытки туннельной спектроскопии». Прогресс в науке о поверхности. 42 (1–4): 101–115. Bibcode:1993ПрСС ... 42..101К. Дои:10.1016/0079-6816(93)90064-3.
- ^ Кляйнт, К. (2004). «Комментарии и ссылки на ранние работы в области автоэлектронной эмиссии». Поверхностный и интерфейсный анализ. 36 (56): 387–390. Дои:10.1002 / sia.1894.
- ^ а б c d Милликен, Р.А.; Айринг, К.Ф. (1926). «Законы, регулирующие вытягивание электронов из металлов в сильных электрических полях». Phys. Rev. 27 (1): 51–67. Bibcode:1926ПхРв ... 27 ... 51М. Дои:10.1103 / PhysRev.27.51.
- ^ Госслинг, Б. С. (1926). «Эмиссия электронов под действием сильных электрических полей». Фил. Mag. 7-я серия. 1 (3): 609–635. Дои:10.1080/14786442608633662.
- ^ Шоттки, В. (Декабрь 1923 г.). "Über kalte und warme Elektronenentladungen". Zeitschrift für Physik A. 14 (63): 63–106. Bibcode:1923ZPhy ... 14 ... 63S. Дои:10.1007 / bf01340034.
- ^ а б c Милликен, Р.А.; Лауритсен, К. (1928). "Связь полевых токов с термоэлектронными токами". PNAS. 14 (1): 45–49. Bibcode:1928ПНАС ... 14 ... 45М. Дои:10.1073 / pnas.14.1.45. ЧВК 1085345. PMID 16587302.
- ^ а б Оппенгеймер, Дж. Р. (1928). «Три заметки по квантовой теории апериодических эффектов». Физический обзор. 31 (1): 66–81. Bibcode:1928ПхРв ... 31 ... 66О. Дои:10.1103 / PhysRev.31.66.
- ^ Yamabe, T .; Тачибана, А .; Сильверстоун, HJ (1977). «Теория ионизации атома водорода внешним электростатическим полем». Физический обзор A. 16 (3): 877–890. Bibcode:1977PhRvA..16..877Y. Дои:10.1103 / PhysRevA.16.877.
- ^ а б c Stern, T.E .; Gossling, B.S .; Фаулер, Р. Х. (1929). «Дальнейшие исследования эмиссии электронов из холодных металлов». Труды Королевского общества А. 124 (795): 699–723. Bibcode:1929RSPSA.124..699S. Дои:10.1098 / rspa.1929.0147. JSTOR 95240.
- ^ Зоммерфельд, А. (1927). "Zur Elektronentheorie der Metalle". Naturwissenschaften. 15 (41): 825. Bibcode:1927NW ..... 15..825S. Дои:10.1007 / BF01505083.
- ^ а б Зоммерфельд, А .; Бет, Х. (1963). "Handbuch der Physik". Юлиус Спрингер-Верлаг. 24.
- ^ Z. Physik 51, 204 (1928) Г. Гамов, "Zur Quantentheorie des Atomkernes".
- ^ Gurney, R.W .; Кондон, Э. (1928). «Волновая механика и радиоактивный распад». Природа. 122 (3073): 439. Bibcode:1928Натура.122..439Г. Дои:10.1038 / 122439a0.
- ^ Gurney, R.W .; Кондон, Э. (1929). «Квантовая механика и радиоактивный распад». Физический обзор. 33 (2): 127–140. Bibcode:1929ПхРв ... 33..127Г. Дои:10.1103 / PhysRev.33.127.
- ^ Кондон, Э. (1978). «Туннелирование - как все начиналось». Американский журнал физики. 46 (4): 319–323. Bibcode:1978AmJPh..46..319C. Дои:10.1119/1.11306.
- ^ Мюллер, E.W. (1937). "Elektronenmikroskopische Beobachtungen von Feldkathoden". Z. Phys. 106 (9–10): 541–550. Bibcode:1937ZPhy..106..541M. Дои:10.1007 / BF01339895.
- ^ Гомер, Р. (1961). Автоэмиссия и полевая ионизация. Кембридж, Массачусетс: Harvard Univ. Нажмите. ISBN 1-56396-124-5.
- ^ Swanson, L.W .; Белл, A.E. (1975). «Последние достижения в области полевой электронной микроскопии металлов». Успехи электроники и электронной физики. 32: 193–309. Дои:10.1016 / S0065-2539 (08) 60236-X. ISBN 9780120145324.
- ^ «Роль адсорбированного состояния в гетерогенном катализе», Обсудить. Faraday Soc., Vol. 41 (1966)
- ^ а б Dyke, W.P .; Тролан, Дж. (1953). «Автоэлектронная эмиссия: большие плотности тока, объемный заряд и вакуумная дуга». Физический обзор. 89 (4): 799–808. Bibcode:1953ПхРв ... 89..799Д. Дои:10.1103 / PhysRev.89.799.
- ^ Dyke, W.P .; Долан, W.W. (1956). «Автоэлектронная эмиссия». Успехи электроники и электронной физики. 8: 89–185. Дои:10.1016 / S0065-2539 (08) 61226-3. ISBN 9780120145089.
- ^ Pandey, AD; Мюллер, Гюнтер; Решке, Детлеф; Певица, Ксения (2009). «Автоэмиссия кристаллического ниобия». Phys. Преподобный ST Accel. Балки. 12 (2): 023501. Bibcode:2009ПхРвС..12б3501Д. Дои:10.1103 / PhysRevSTAB.12.023501.
- ^ а б c Abbott, F. R .; Хендерсон, Джозеф Э. (1939). «Диапазон и применимость уравнения тока поля». Физический обзор. 56 (1): 113–118. Bibcode:1939ПхРв ... 56..113А. Дои:10.1103 / PhysRev.56.113.
- ^ а б c d Янг, Рассел Д. (1959). «Теоретическое распределение полевых электронов по полной энергии». Физический обзор. 113 (1): 110–114. Bibcode:1959ПхРв..113..110Л. Дои:10.1103 / PhysRev.113.110.
- ^ Янг, Рассел Д.; Мюллер, Эрвин В. (1959). "Экспериментальное измерение распределения полевых электронов по полной энергии". Физический обзор. 113 (1): 115–120. Bibcode:1959ПхРв..113..115л. Дои:10.1103 / PhysRev.113.115.
- ^ а б c d е ж грамм А. Модинос (1984). Полевая, термоэлектронная и эмиссионная спектроскопия вторичных электронов. Пленум, Нью-Йорк. ISBN 0-306-41321-3.
- ^ а б c d е Gadzuk, J. W .; Пламмер, Э. У. (1973). «Распределение энергии полевых выбросов (FEED)». Обзоры современной физики. 45 (3): 487–548. Bibcode:1973РвМП ... 45..487Г. Дои:10.1103 / RevModPhys.45.487.
- ^ Crewe, A. V .; Wall, J .; Лэнгмор, Дж. (1970). «Видимость одиночных атомов». Наука. 168 (3937): 1338–40. Bibcode:1970Sci ... 168.1338C. Дои:10.1126 / science.168.3937.1338. PMID 17731040.
- ^ Шарбонье, Ф (1996). «Разработка и использование полевого эмиттера в качестве источника электронов высокой интенсивности». Прикладная наука о поверхности. 94-95: 26–43. Bibcode:1996ApSS ... 94 ... 26C. Дои:10.1016 / 0169-4332 (95) 00517-Х.
- ^ а б Орлофф, изд. (2008). Справочник по оптике заряженных частиц (2-е изд.). CRC Press.
- ^ Л.В. Свонсон, А.Е. Белл, Adv. Электрон. Электронная физика. 32 (1973) 193
- ^ Суонсон, Л. У. (1975). «Сравнительное исследование циркониевого и наплавленного катода с тепловым полем из W». Журнал вакуумной науки и техники. 12 (6): 1228. Bibcode:1975JVST ... 12.1228S. Дои:10.1116/1.568503.
- ^ а б c d Милн В.И.; и другие. (Сентябрь 2008 г.). "Информационный бюллетень E nano" (13). Цитировать журнал требует
| журнал =(помощь) - ^ а б Де Йонге, Нильс; Бонар, Жан-Марк (2004). «Источники электронов из углеродных нанотрубок и их применение». Философские труды Королевского общества A. 362 (1823): 2239–66. Bibcode:2004RSPTA.362.2239D. Дои:10.1098 / rsta.2004.1438. PMID 15370480.
- ^ а б П.В. Хоукс; Э. Каспар (1996). «44,45». Принципы электронной оптики. 2. Academic Press, Лондон.
- ^ Dyke, W. P .; Trolan, J. K .; Dolan, W. W .; Барнс, Джордж (1953). «Полевой эмиттер: изготовление, электронная микроскопия и расчеты электрического поля». Журнал прикладной физики. 24 (5): 570. Bibcode:1953JAP .... 24..570D. Дои:10.1063/1.1721330.
- ^ Эверхарт, Т. Э. (1967). «Упрощенный анализ источников электронов с точечным катодом». Журнал прикладной физики. 38 (13): 4944. Bibcode:1967JAP .... 38.4944E. Дои:10.1063/1.1709260.
- ^ Визнер, Дж. К. (1973). «Источники электронов с точечным катодом - электронная оптика начальной диодной области». Журнал прикладной физики. 44 (5): 2140. Bibcode:1973JAP .... 44,2140 Вт. Дои:10.1063/1.1662526.
- ^ Визнер, Дж. К. (1974). "Источники электронов с точечным катодом. Электронная оптика начальной области диода: исправления и дополнения". Журнал прикладной физики. 45 (6): 2797. Bibcode:1974JAP .... 45,2797 Вт. Дои:10.1063/1.1663676.
- ^ а б Финк, Ханс-Вернер (1988). «Точечный источник ионов и электронов». Physica Scripta. 38 (2): 260–263. Bibcode:1988 ФИЗЫ ... 38..260F. Дои:10.1088/0031-8949/38/2/029.
- ^ а б Ward, B.W .; Notte, John A .; Эконому, Н. П. (2006). «Гелиевый ионный микроскоп: новый инструмент для наноразмерной микроскопии и метрологии». Журнал вакуумной науки и техники B. 24 (6): 2871. Bibcode:2006JVSTB..24.2871W. Дои:10.1116/1.2357967. S2CID 55043024.
- ^ Бинь, Ву Тхиен; Garcia, N .; Перселл, С. (1996). «Эмиссия электронного поля из источников атомов: изготовление, свойства и применение наноструктур». Достижения в области визуализации и электронной физики. 95: 63–153. Дои:10.1016 / S1076-5670 (08) 70156-3. ISBN 9780120147373.
- ^ а б c Шпиндт, К. А. (1976). «Физические свойства тонкопленочных автоэмиссионных катодов с молибденовыми конусами». Журнал прикладной физики. 47 (12): 5248–5263. Bibcode:1976JAP .... 47.5248S. Дои:10.1063/1.322600.
- ^ а б c Р.В. Латам, изд. (1995). Высоковольтная вакуумная изоляция: основные понятия и технологическая практика. Академический, Лондон.
- ^ Форбс, Р. (2001). «Электронная эмиссия с низким макроскопическим полем из углеродных пленок и других электрически наноструктурированных гетерогенных материалов: гипотезы о механизме эмиссии». Твердотельная электроника. 45 (6): 779–808. Bibcode:2001ССЭле..45..779Ф. Дои:10.1016 / S0038-1101 (00) 00208-2.
- ^ Робертсон, Дж (2002). «Алмазоподобный аморфный углерод». Материаловедение и инженерия: R: Отчеты. 37 (4–6): 129–281. Дои:10.1016 / S0927-796X (02) 00005-0.
- ^ S.R.P. Сильва; Дж. Д. Кэри; R.U.A. Хан; НАПРИМЕР. Герстнер; J.V. Anguita (2002). «9». В H.S. Налва (ред.). Справочник по тонкопленочным материалам. Академический, Лондон.
- ^ Ходжати-Талеми, П .; Саймон, Г. (2011). «Автоэмиссионные исследования графеновых наностенок, полученных микроволново-плазменным методом». Углерод. 49 (8): 2875–2877. Дои:10.1016 / j.carbon.2011.03.004.
- ^ Сюй, N; Huq, S (2005). «Новые материалы и приложения с холодным катодом». Материаловедение и инженерия: R: Отчеты. 48 (2–5): 47–189. Дои:10.1016 / j.mser.2004.12.001.
- ^ а б Ходжати-Талеми, Педжман; Хокинс, Стивен; Huynh, Chi; Саймон, Джордж П. (2013). «Понимание параметров, влияющих на свойства автоэмиссии непосредственно прядильных полотен углеродных нанотрубок». Углерод. 57: 388–394. Дои:10.1016 / j.carbon.2013.01.088.
- ^ а б Ходжати-Талеми, Педжман; Хокинс, Стивен С.; Huynh, Chi P .; Саймон, Джордж П. (2013). «Высокоэффективная низковольтная электронная эмиссия из непосредственно прядильных полотен углеродных нанотрубок». Углерод. 57: 169–173. Дои:10.1016 / j.carbon.2013.01.060.
- ^ Кузнецов, Александр А .; Ли, Сергей Б .; Чжан, Мэй; Baughman, Ray H .; Захидов, Анвар А. (2010). «Автоэлектронная эмиссия из прозрачных многослойных листов углеродных нанотрубок для инвертированных автоэмиссионных дисплеев». Углерод. 48: 41–46. Дои:10.1016 / j.carbon.2009.08.009.
- ^ а б Х. Крейг Миллер (ноябрь 2003 г.). "Библиография: электрические разряды в вакууме: 1877-2000 гг.". Архивировано из оригинал 13 ноября 2007 г.
- ^ Родерик, Э. (1978). Контакты металл-полупроводник. Оксфорд: Clarendon Press. ISBN 0-19-859323-6.
- ^ Форбс, Р. (1999). «Электрическая поверхность как центр тяжести поверхностно-индуцированного заряда». Ультрамикроскопия. 79 (1–4): 25–34. Дои:10.1016 / S0304-3991 (99) 00098-4.
- ^ а б Херринг, Коньерс; Николс, М. (1949). «Термоэмиссия». Обзоры современной физики. 21 (2): 185–270. Bibcode:1949РвМП ... 21..185Н. Дои:10.1103 / RevModPhys.21.185.
- ^ В. Шоттки (1914). Phys. Z. 15: 872. Отсутствует или пусто
| название =(помощь) - ^ а б Л.В. Нордхайм (1928). «Влияние силы изображения на излучение и отражение электронов металлами». Труды Королевского общества А. 121 (788): 626–639. Bibcode:1928RSPSA.121..626N. Дои:10.1098 / rspa.1928.0222.
- ^ Х. Джеффрис (1924). "О некоторых приближенных решениях линейных дифференциальных уравнений второго порядка". Труды Лондонского математического общества. 23: 428–436. Дои:10.1112 / плмс / с2-23.1.428.
- ^ а б c Форбс, Ричард Г. (2008). «О необходимости туннельного предварительного фактора в теории туннелирования Фаулера – Нордхейма» (PDF). Журнал прикладной физики. 103 (11): 114911–114911–8. Bibcode:2008JAP ... 103k4911F. Дои:10.1063/1.2937077.
- ^ Х. Фрёман, П.О. Фроман, "Приближение JWKB: вклад в теорию" (Северная Голландия, Амстердам, 1965).
- ^ а б c d е ж грамм час Forbes, Ричард Дж .; Дин, Джонатан Х. (2007). «Переформулировка стандартной теории туннелирования Фаулера – Нордхейма и эмиссии холодных полевых электронов». Труды Королевского общества А. 463 (2087): 2907–2927. Bibcode:2007RSPSA.463.2907F. Дои:10.1098 / rspa.2007.0030.
- ^ Дин, Джонатан Н. Б.; Форбс, Ричард Дж. (2008). «Формальный вывод точного разложения в ряд для основной барьерной функции Шоттки – Нордхейма с использованием гипергеометрического дифференциального уравнения Гаусса». Журнал физики A: математический и теоретический. 41 (39): 395301. Bibcode:2008JPhA ... 41M5301D. Дои:10.1088/1751-8113/41/39/395301.
- ^ а б Берджесс, Р. Э .; Хьюстон, Дж. М .; Хьюстон, Дж. (1953). «Скорректированные значения полевых эмиссионных функций Фаулера-Нордхейма v (y) и s (y)». Физический обзор. 90 (4): 515. Bibcode:1953ПхРв ... 90..515Б. Дои:10.1103 / PhysRev.90.515.
- ^ а б c Мерфи, E. L .; Хорошо, Р. Х. (1956). «Термионная эмиссия, полевая эмиссия и переходная область». Физический обзор. 102 (6): 1464–1473. Bibcode:1956ПхРв..102.1464М. Дои:10.1103 / PhysRev.102.1464.
- ^ а б c d Форбс, Ричард Г. (2004). «Использование пространственно-энергетических диаграмм в свободных электронах моделей автоэлектронной эмиссии». Поверхностный и интерфейсный анализ. 36 (56): 395–401. Дои:10.1002 / sia.1900.
- ^ Градштейн и Рыжик (1980). Таблицы интегралов, серий и продуктов. Академический, Нью-Йорк. см. формулу 3.241 (2), где μ=1
- ^ а б Модинос, А (2001). «Теоретический анализ данных автоэмиссии». Твердотельная электроника. 45 (6): 809–816. Bibcode:2001ССЭле..45..809М. Дои:10.1016 / S0038-1101 (00) 00218-5.
- ^ Форбс, Ричард Г. (2008). «Физика обобщенных уравнений типа Фаулера-Нордгейма». Журнал вакуумной науки и техники B. 26 (2): 788. Bibcode:2008JVSTB..26..788F. Дои:10.1116/1.2827505.
- ^ Форбс, Ричард Г. (2008). «Описание вольт-амперных характеристик автоэлектронной эмиссии в терминах масштабированных значений барьерного поля (f-значения)». Журнал вакуумной науки и техники B. 26 (1): 209. Bibcode:2008JVSTB..26..209F. Дои:10.1116/1.2834563.
- ^ Л.В. Нордхайм (1928). "Zur Theorie der thermischen Emission und der Reflexion von Elektronen an Metallen". Z. Phys. 46 (11–12): 833–855. Bibcode:1928ZPhy ... 46..833N. Дои:10.1007 / BF01391020.
- ^ Страттон, Роберт (1962). «Теория полевой эмиссии полупроводников». Физический обзор. 125 (1): 67–82. Bibcode:1962ПхРв..125 ... 67С. Дои:10.1103 / PhysRev.125.67.
- ^ Форбс, Ричард Г. (2008). «Точный анализ уменьшения поверхностного поля из-за испускаемого полем вакуумного пространственного заряда в геометрии параллельной плоскости с использованием простых безразмерных уравнений» (PDF). Журнал прикладной физики. 104 (8): 084303–084303–10. Bibcode:2008JAP ... 104х4303Ф. Дои:10.1063/1.2996005.
- ^ Forbes, R; Edgcombe, CJ; Вальдре, У (2003). «Некоторые комментарии к моделям для улучшения поля». Ультрамикроскопия. 95 (1–4): 57–65. Дои:10.1016 / S0304-3991 (02) 00297-8. PMID 12535545.
- ^ Smith, R.C .; Форрест, Р. Д .; Кэри, Дж. Д .; Hsu, W. K .; Сильва, С. Р. П. (2005). «Интерпретация коэффициента усиления неплоских полевых излучателей» (PDF). Письма по прикладной физике. 87 (1): 013111. Bibcode:2005АпФЛ..87а3111С. Дои:10.1063/1.1989443.
- ^ а б c d Кирицакис, А .; Ксантакис, Дж. П. (2015). «Вывод обобщенного уравнения Фаулера-Нордгейма для наноскопических полевых излучателей». Труды Королевского общества А. 471 (2174): 20140811. Bibcode:2015RSPSA.47140811K. Дои:10.1098 / rspa.2014.0811.
- ^ He, J .; Катлер, П. Х. (1991). «Вывод обобщенного уравнения Фаулера-Нордхейма для наноскопических полевых эмиттеров». Письма по прикладной физике. 59 (13): 1644. Bibcode:1991ApPhL..59.1644H. Дои:10.1063/1.106257.
- ^ Fursey, G.N .; Глазанов, Д. В. (1998). «Отклонения от теории Фаулера – Нордхейма и особенности автоэлектронной эмиссии мелкомасштабных объектов». Журнал вакуумной науки и техники B. 16 (2): 910. Bibcode:1998JVSTB..16..910F. Дои:10.1116/1.589929.
- ^ Cabrera, H .; и другие. (2013). «Масштабная инвариантность диодоподобного туннельного перехода». Физический обзор B. 87 (11): 115436. arXiv:1303.4985. Bibcode:2013PhRvB..87k5436C. Дои:10.1103 / PhysRevB.87.115436.
- ^ Кирицакис, А .; Джурабекова, Ф. (2017). «Общий вычислительный метод для электронной эмиссии и тепловых эффектов в излучающих поле наноостриях». Вычислительное материаловедение. 128: 15. arXiv:1609.02364. Дои:10.1016 / j.commatsci.2016.11.010.
- ^ Форбс, Ричард Г. (2008). «Запрос на экспериментальную проверку переработанной математической формы эмпирических вольт-амперных характеристик автоэмиссии» (PDF). Письма по прикладной физике. 92 (19): 193105. Bibcode:2008АпФЛ..92с3105Ф. Дои:10.1063/1.2918446.
- ^ Дженсен, К. Л. (1999). «Обменно-корреляционные, дипольные и зарядовые потенциалы для источников электронов: изменение высоты барьера по температуре и полю». Журнал прикладной физики. 85 (5): 2667. Bibcode:1999JAP .... 85.2667J. Дои:10.1063/1.369584.
- ^ Т. Кирк, 21-й стажер. Конференция по вакуумной наноэлектронике, Вроцлав, июль 2008 г.
- ^ Модинос, А (1974). «Автоэмиссия из поверхностных состояний в полупроводниках». Наука о поверхности. 42 (1): 205–227. Bibcode:1974СурСк..42..205М. Дои:10.1016/0039-6028(74)90013-2.
дальнейшее чтение
Общая информация
- W. Zhu, ed. (2001). Вакуумная микроэлектроника. Вили, Нью-Йорк.
- Г. Ферси (2005). Полевая эмиссия в вакуумной микроэлектронике. Kluwer Academic, Нью-Йорк. ISBN 0-306-47450-6.
Проникновение поля и изгиб ленты (полупроводники)
- Сейвац, Рут; Грин, Мино (1958). «Расчеты космического заряда полупроводников». Журнал прикладной физики. 29 (7): 1034. Bibcode:1958JAP .... 29.1034S. Дои:10.1063/1.1723358.
- А.Мани, Ю.Гольдштейн, Н.Б. Гровер, Поверхности полупроводников (Северная Голландия, Амстердам, 1965).
- W. Mönsch, Поверхности полупроводников и интерфейсы (Springer, Берлин, 1995).
- Пэн, Цзе; Ли, Чжибин; Он, Чуньшань; Чен, Гуйхуа; Ван, Вэйлян; Дэн, Шаочжи; Сюй, Ниншэн; Чжэн, Сяо; Чен, Гуаньхуа; Edgcombe, Крис Дж .; Форбс, Ричард Г. (2008). «Роль апексных диполей и проникновения поля в физике заряженных, излучающих поле, однослойных углеродных нанотрубок». Журнал прикладной физики. Издательство AIP. 104 (1): 014310. arXiv:cond-mat / 0612600. Дои:10.1063/1.2946449. ISSN 0021-8979.
Полевой вакуум объемный заряд
- Barbour, J. P .; Dolan, W. W .; Trolan, J. K .; Martin, E. E .; Дайк, У. П. (1953). «Эффекты пространственного заряда в полевой эмиссии». Физический обзор. 92 (1): 45–51. Bibcode:1953ПхРв ... 92 ... 45Б. Дои:10.1103 / PhysRev.92.45.
Автоэмиссия при высоких температурах и фотоэмиссия
- Дженсен, Кевин (2007). Физика электронной эмиссии. Достижения в области визуализации и электронной физики. 149. Сан-Диего: Academic Press. ISBN 978-0-12-374207-0. OCLC 647688316.
Индуцированный полем взрывная электронная эмиссия
- Г.А. Месяц, Взрывная электронная эмиссия, УРО Пресс, Екатеринбург (1998).

![{ frac { hbar ^ {2}} {2m}} { frac {{ mathrm {d}} ^ {2} Psi (x)} {{ mathrm {d}} x ^ {2}} } = left [U (x) -E _ {{{ mathrm {n}}}} right] Psi (x) = M (x) Psi (x), qquad qquad (1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/eacff3dd80d79ed688b50ebd7ff97c384d88c73a)















![D (h, F) приблизительно P exp left [- { frac { nu (h, F) bh ^ {{3/2}}} {F}} right], qquad qquad (15 )](https://wikimedia.org/api/rest_v1/media/math/render/svg/1160ba66f6babbc1b0a4f20921baff0c0aff3d7b)

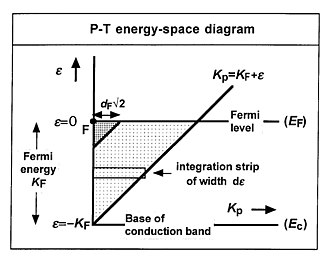



![, f _ {{{ mathrm {FD}}}} ( epsilon) = 1 / [1 + { mathrm {exp}} ( epsilon / k _ {{{ mathrm {B}}}} T)] , ........... (18)](https://wikimedia.org/api/rest_v1/media/math/render/svg/364e81d0e1b49b1fdfd8562f0605efd789021348)



![j ( epsilon) { mathrm {d}} epsilon = z _ {{{ mathrm {S}}}} f _ {{{ mathrm {FD}}}} left [ int D { mathrm {d }} K _ {{{ mathrm {p}}}} right] { mathrm {d}} epsilon = z _ {{{ mathrm {S}}}} f _ {{{ mathrm {FD}}} } D _ {{{ mathrm {F}}}} { mathrm {exp}} ( epsilon / d _ {{{ mathrm {F}}}}) left [ int _ {{0}} ^ { { infty}} { mathrm {exp}} (- K _ {{{ mathrm {p}}}} / d _ {{{ mathrm {F}}}}) ; { mathrm {d}} K_ {{{ mathrm {p}}}} right] { mathrm {d}} epsilon ........... (20)](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e42c470d4d5a58f8815095aed8776f725c7bb42)



![j _ {{{ mathrm {F}}}} [, = z _ {{{ mathrm {S}}}} d _ {{{ mathrm {F}}}} D _ {{{ mathrm {F}} }}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3027bd63c37a2b4cd18c7e5012f8b2b41ada7d)




![Z _ {{{ mathrm {F}}}} ; [= z _ {{{ mathrm {S}}}} {d _ {{{ mathrm {F}}}}} ^ {2}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb68413338808e05643c49192e35aec75fe3a1b)


![{ Displaystyle J = J_ {0} int _ {- infty} ^ { infty} { frac { mathrm {exp} ( epsilon / d _ { mathrm {F}})} {1+ mathrm {exp} [( epsilon / d _ { mathrm {F}}) (d _ { mathrm {F}} / k _ { mathrm {B}} T)]}} mathrm {d} ( epsilon / d_ { mathrm {F}}) = lambda _ {T} J_ {0}, .......... (26)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ffca5c2b045b631db2776defdb513fae83b1987)






![J ; = lambda _ {Z} a phi ^ {{- 1}} F ^ {2} P _ {{{ mathrm {F}}}} { mathrm {exp}} [- nu _ { {{ mathrm {F}}}} b phi ^ {{3/2}} / F], .......... (29)](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8946e3374dca18653406e9db1b64179e3dfc037)

![J = ; a { phi ^ {{- 1}}} F ^ {2} { mathrm {exp}} [- v (f) ; b phi ^ {{3/2}} / F] , .......... (30а)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7840b6453e7bf1a7a2b03e4f52db2835476f15b)





![i = ; A _ {{{ mathrm {r}}}} a { phi ^ {{- 1}}} { beta} ^ {2} V ^ {2} { mathrm {exp}} [- v (f) ; b phi ^ {{3/2}} / beta V], .......... (33)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f44227d58ac00266fbabeb907755627072c21bd4)


![J _ {{{ mathrm {M}}}} = alpha _ {{{ mathrm {r}}}} a { phi ^ {{- 1}}} F ^ {2} { mathrm {exp} } [- v (f) ; b phi ^ {{3/2}} / F], .......... (36)](https://wikimedia.org/api/rest_v1/media/math/render/svg/0547cb98387444e340df063c1c18a6798fbf9fd0)
![i = ; alpha _ {{{ mathrm {r}}}} A _ {{{ mathrm {M}}}} a { phi ^ {{- 1}}} { beta} ^ {2} V ^ {2} { mathrm {exp}} [- v (f) ; b phi ^ {{3/2}} / beta V], .......... (37)](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d98faa9cf4d6b959504793bfa4d5f9e19102faa)












![{ Displaystyle Phi (x) = Fx left [1 - { frac {x} {R}} + O left ({ frac {x} {R}} right) ^ {2} right] { text {, for}} x ll R { text {.}} .......... (42)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0219c638b4a2cfa3b99d6b9f35898fe26e64b30)








![{ displaystyle J = a { frac {F ^ {2}} { phi}} left ({ frac {1} { lambda _ {d} (f)}} + { frac { phi} {eFR}} psi (f) right) ^ {- 2} exp left [- { frac {b phi ^ {3/2}} {F}} left (v (f) + omega (f) { frac { phi} {eFR}} right) right] .......... (46)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f185a159adbc42db55e3bc1ad655eebc0c54801)






![{ displaystyle i = ; CV ^ { kappa} mathrm {exp} [-B / V], .......... (48)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9eab1d34efd87383ece6cc8fdb0f4a0366e3c99)


![{ Displaystyle mathrm {exp} [-v (f) ; b { phi} ^ {3/2} / F] ; = ; mathrm {exp} [-v (f) ; eta / f] ; приблизительно ; { mathrm {e}} ^ { eta} f ^ {- eta / 6} mathrm {exp} [- eta / f] ; = ; { mathrm {e}} ^ { eta} f ^ {- eta / 6} mathrm {exp} [-b { phi} ^ {3/2} / F] ........... (51)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58050354d9f1f073fbd6fd108337f79cee7b6b5c)






