WikiDer > Шестиугольная решетка

Hexagonal lattice
Не путать с Семейство гексагональных кристаллов.
Равносторонний треугольник Lattice.svgРешетка равностороннего треугольника rotated.svg
Шестиугольная или треугольная решетка точек в двух ориентациях.
Треугольная черепица. Вершины образуют шестиугольную решетку с горизонтальными рядами с треугольниками, направленными вверх и вниз. Треугольники можно сгруппировать 6 на 6 тремя способами, чтобы получился шестиугольная черепица. В каждом случае шестиугольники ориентированы двумя горизонтальными сторонами и расположены вертикальными рядами, и в каждом случае у них есть темный треугольник в верхнем левом углу.

В шестиугольная решетка или же треугольная решетка один из пяти 2D решетка типы.

Три соседние точки образуют равносторонний треугольник. На изображениях четыре ориентации такого треугольника являются наиболее распространенными. Их можно удобно назвать, рассматривая треугольник как стрелку, указывающую вверх, вниз, влево или вправо; хотя в каждом случае их можно также рассматривать как указывающие в двух наклонных направлениях.

Наиболее распространены две ориентации изображения решетки. Их можно удобно назвать «гексагональной решеткой с горизонтальными рядами» (как на рисунке ниже), с треугольниками, направленными вверх и вниз, и «гексагональной решеткой с вертикальными рядами», с треугольниками, указывающими влево и вправо. Они различаются на угол 30 °.

Гексагональная решетка с горизонтальными рядами представляет собой частный случай центрированной прямоугольной (т. Е. Ромбической) решетки с прямоугольниками, которые √3 раз выше ширины. Конечно, для другой ориентации прямоугольники √3 раз в ширину.

Его симметрия категория группа обоев p6m. Узор с этой решеткой из поступательная симметрия не может иметь больше, но может иметь меньшую симметрию, чем сама решетка.

Шестиугольная черепица, соты структура. Центры шестиугольников образуют шестиугольную решетку с вертикальными рядами; для каждого цвета центры шестиугольников этого цвета образуют шестиугольную решетку с горизонтальными рядами, которая находится в линейном масштабе √3 раз больше. Вершины всех шестиугольников вместе с их центрами образуют шестиугольную решетку с горизонтальными рядами, имеющую линейный масштаб. √3 раз меньше первой решетки.

Для изображения соты Структура, опять же, две ориентации являются наиболее распространенными. Их можно удобно назвать «сотовой структурой с горизонтальными рядами» с шестиугольниками с двумя вертикальными сторонами и «сотовой структурой с вертикальными рядами» с шестиугольниками с двумя горизонтальными сторонами. Они различаются на угол 90 °, что эквивалентно 30 °.

Сотовая структура двояко связана с гексагональной решеткой:

  • центры шестиугольников соты образуют шестиугольную решетку, ряды которой ориентированы одинаково
  • вершины сот вместе со своими центрами образуют гексагональную решетку, повернутую на 30 ° (или, что эквивалентно, 90 °) и масштабируемую с коэффициентом относительно другой решетки

Отношение количества вершин к количеству шестиугольников равно 2, поэтому вместе с центрами соотношение равно 3, обратной величине квадрата масштабного коэффициента.

Период, термин сотовая решетка может означать соответствующую гексагональную решетку или структуру, которая не является решеткой в группа смысл, но например один в смысле решетчатая модель. Набор точек, образующих вершины сот (без точек в центрах), показывает сотовую структуру. Его можно рассматривать как объединение двух смещенных треугольных решеток, показанных здесь красным и синим.

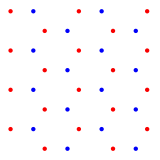Расположение вершин шестиугольного тайла 2-color.svg
2 треугольные решетки		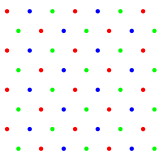Решетка равностороннего треугольника 3-color.svg
3 треугольные решетки

Сама треугольная решетка может быть разделена на 3 треугольные решетки со смещением, показанные выше красным, зеленым и синим цветом. Треугольную решетку еще называют Решетка А2, А2,[1] а объединение трех треугольных решеток есть A*2.[2]

Изображение p6m, показывающее (также для p6) 6-кратные ротоцентры (центры шестиугольников), 3-кратные (центры треугольников) и, в частности, 2-кратные ротоцентры (вершины). 3-кратные ротоцентры расположены в сотовой структуре, а центры вращения 2-го порядка образуют маленькие треугольники вокруг них, соприкасаются друг с другом, а также образуют шестиугольники, повернутые на 30 ° и немного меньше: в линейном масштабе коэффициент (1 / 2) √3 раз больше.

В дополнение к этим точкам или вместо них могут быть показаны стороны шестиугольников; в зависимости от приложения они могут называться решетчатые связи.

Относительно гексагональной решетки мы можем выделить два множества или три направления:

  • направления наименьшего расстояния между узлами решетки; назовем их основными направлениями перевода
  • направления второго наименьшего расстояния между точками решетки; назовем их вторичными направлениями перевода; эти расстояния √3 раз больше. Набор точек решетки можно разделить на три набора с этими большими расстояниями перемещения.

Внутри каждого набора направлений направления различаются на угол 60 °, а между наборами - на углы от 30 ° до 90 °. Для шестиугольной решетки с горизонтальными рядами одно из трех направлений является горизонтальным, а для шестиугольной решетки с вертикальными рядами одно из трех направлений является вертикальным.

И наоборот, для данной решетки мы можем создать повернутую решетку, которая √3 раз точнее, добавив центры равносторонних треугольников. Так как треугольников вдвое больше, чем вершин, это утроит количество вершин.

Расположение в примитивной ячейке 2-, 3- и 6-кратных ротоцентров, по отдельности или в комбинации (рассматривайте 6-кратный символ как комбинацию 2- и 3-кратного символа). Для случая p6m основная область обозначена желтым цветом.

Узор с 3- или 6-кратным вращательная симметрия имеет решетку из 3-кратных ротоцентров (включая возможные 6-кратные ротоцентры), которая является этой более тонкой решеткой относительно решетки поступательная симметрия.

В случае 6-кратной вращательной симметрии 6-кратные центры образуют решетку столь же крупную, как решетка трансляционной симметрии, то есть есть один 6-кратный центр и есть два 3-кратных центра на примитивную ячейку.

Для осей отражения есть два возможных набора направлений, упомянутых выше. В случае 3-кратной симметрии не применяется ни одно из значений (p3) или одно из двух:

  • p3m1 с осями отражения по кратчайшим связям между ротоцентрами
  • p31m по основным направлениям перевода

В 6-кратном случае применимо либо ни одно (p6), либо оба (p6m).

Если есть оси отражения в основных направлениях перемещения, один из трех наборов ротоцентров играет иную роль, чем два других: эти оси отражения проходят через них. С p6 один сет особенный, потому что он 6-разовый.

Шестиугольная черепица Hexakis, пример p6 (с цветами) и p6m (без); линии являются осями отражения, если цвета игнорируются, и осью симметрии особого вида, если цвета не игнорируются: отражение меняет цвета. Можно выделить прямоугольные линейные сетки в трех ориентациях.

Смотрите также

Рекомендации

  1. ^ http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/A2.html
  2. ^ http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/As2.html
  • Борн, М .: «Об устойчивости кристаллических решеток. IX. Ковариантная теория деформаций решетки и устойчивость некоторых гексагональных решеток». Труды Кембриджского философского общества 38, (1942). 82–99.