WikiDer > Икосаэдрическая призма
| Икосаэдрическая призма | |
|---|---|
| Тип | Призматический однородный 4-многогранник |
| Единый индекс | 59 |
| Символ Шлефли | т0,3{3,5,2} или {3,5} × {} с {3,4} × {} sr {3,3} × {} |
| Кокстер-Дынкин | |
| Клетки | 2 (3.3.3.3.3) 20 (3.4.4) |
| Лица | 30 {4} 40 {3} |
| Края | 72 |
| Вершины | 24 |
| Фигура вершины | 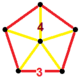 Правильно-пятиугольная пирамида |
| Группа симметрии | [5,3,2], заказ 240 [3+, 4,2], порядок 48 [(3,3)+, 2], порядок 24 |
| Характеристики | выпуклый |
В геометрия, икосаэдрическая призма выпуклый равномерный 4-многогранник (четырехмерный многогранник). Этот 4-многогранник имеет 22 многогранник ячеек: 2 икосаэдры связаны 20 треугольные призмы. У него 70 граней: 30 квадратов и 40 треугольников. У него 72 ребра и 24 вершины.
Его можно построить, создав два совпадающих икосаэдра в 3-м пространстве и перемещая каждую копию в противоположных перпендикулярных направлениях в 4-м пространстве, пока их расстояние не станет равным длине их ребер.
Это один из 18 выпуклых однородные многогранные призмы создан с использованием униформы призмы для соединения пар параллельно Платоновы тела или же Архимедовы тела.
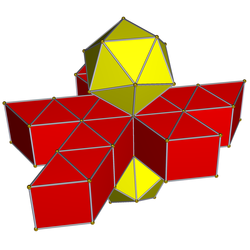 Сеть | 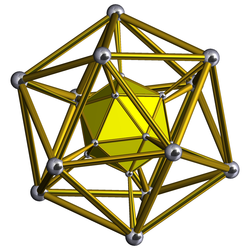 Диаграмма Шлегеля Показана только одна икосаэдрическая ячейка |
Альтернативные имена
- Икосаэдрическая диадическая призма Норман В. Джонсон
- Ipe для икосаэдрической призмы / гиперпризмы (Джонатан Бауэрс)
- Плоскостная тетраэдрическая призма / гиперпризма
Связанные многогранники
- Курносая тетраэдрическая антипризма - = ht0,1,2,3{3,3,2} или






 , родственный неоднородный 4-многогранник
, родственный неоднородный 4-многогранник
внешняя ссылка
- 6. Выпуклая однородная призматическая полихора - Модель 59., Георгий Ольшевский.
- Клитцинг, Ричард. "4D однородные многогранники (полихоры) x o3o5x - ipe".
| Этот 4-многогранник статья - это заглушка. Вы можете помочь Википедии расширяя это. |
