WikiDer > Иллюстрация центральной предельной теоремы

Illustration of the central limit theorem

В теории вероятностей Центральная предельная теорема (CLT) утверждает, что во многих ситуациях, когда добавляются независимые случайные величины, их правильно нормализованная сумма стремится к нормальному распределению. Эта статья дает две иллюстрации этой теоремы. Оба включают в себя сумму независимые и одинаково распределенные случайные величины и показать, как распределение вероятностей суммы приближается к нормальное распределение по мере увеличения количества слагаемых в сумме.

Первая иллюстрация включает непрерывное распределение вероятностей, для которых случайные величины имеют функция плотности вероятности. Вторая иллюстрация, для которой большая часть вычислений может быть выполнена вручную, включает в себя дискретное распределение вероятностей, который характеризуется функция массы вероятности.

Иллюстрация непрерывного случая

В плотность суммы двух независимых вещественных случайных величин равно свертка функций плотности исходных переменных.

Таким образом, плотность суммы м+п членов последовательности независимых одинаково распределенных переменных равняется свертке плотностей сумм м сроки и п срок. В частности, плотность суммы п+1 член равен свертке плотности суммы п члены с исходной плотностью («сумма» 1 члена).

А функция плотности вероятности показан на первом рисунке ниже. Тогда плотности сумм двух, трех и четырех независимые одинаково распределенные переменные, каждая из которых имеет исходную плотность, показаны на следующих рисунках. кусочно многочлен, как в примере, так и суммарные плотности все более высокой степени. Хотя исходная плотность далека от нормы, плотность суммы всего нескольких переменных с этой плотностью намного более гладкая и имеет некоторые качественные особенности нормальная плотность.

Свертки были вычислены с помощью дискретное преобразование Фурье. Список ценностей у = ж(Икс₀ + k ΔИкс), где ж - исходная функция плотности, а ΔИкс примерно равно 0,002, а k равно от 0 до 1000. Дискретное преобразование Фурье Y из у был вычислен. Тогда свертка ж с собой пропорциональна обратному дискретному преобразованию Фурье точечный продукт из Y с собой.

Функция плотности вероятности.

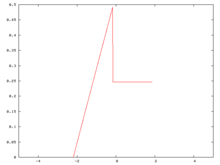
Исходная функция плотности вероятности

Начнем с функции плотности вероятности. Эта функция, хотя и прерывистая, далеко не самый патологический пример, который можно было бы создать. Это кусочный многочлен с частями степеней 0 и 1. Среднее значение этого распределения равно 0, а его стандартное отклонение равно 1.

Плотность суммы двух переменных.

Функция плотности вероятности суммы двух членов

Затем мы вычисляем плотность суммы двух независимых переменных, каждая из которых имеет указанную выше плотность. Плотность суммы равна свертка вышеупомянутой плотности с собой.

Сумма двух переменных имеет среднее значение 0. Плотность, показанная на рисунке справа, была изменена на ${ displaystyle { sqrt {2}}}$ , так что его стандартное отклонение равно 1.

Эта плотность уже более гладкая, чем исходная, есть явные комочки, соответствующие интервалам, на которых определялась исходная плотность.

Плотность суммы трех переменных.

Функция плотности вероятности суммы трех членов

Затем мы вычисляем плотность суммы трех независимых переменных, каждая из которых имеет указанную выше плотность. Плотность суммы - это свертка первой плотности со второй.

Сумма трех переменных имеет среднее значение 0. Плотность, показанная на рисунке справа, была изменена на √3, так что его стандартное отклонение равно 1.

Эта плотность даже более гладкая, чем предыдущая, комочки на этом рисунке практически не видны.

Плотность суммы четырех переменных

Функция плотности вероятности суммы четырех членов

Наконец, мы вычисляем плотность суммы четырех независимых переменных, каждая из которых имеет указанную выше плотность. Плотность суммы - это свертка первой плотности с третьей (или второй плотности с самой собой).

Сумма четырех переменных имеет среднее значение 0. Плотность, показанная на рисунке справа, была изменена на √4, так что его стандартное отклонение равно 1.

Эта плотность выглядит качественно очень похожей на нормальную плотность, никаких комков не различить на глаз.

Иллюстрация дискретного случая

В этом разделе проиллюстрирована центральная предельная теорема на примере, для которого вычисления могут выполняться быстро вручную на бумаге, в отличие от примера с более интенсивными вычислениями из предыдущего раздела.

Сумма всех перестановок длины 1, выбранных из набора целых чисел 1, 2, 3

Исходная функция массы вероятности

Предположим, что распределение вероятностей дискретная случайная величина Икс ставит одинаковые веса на 1, 2 и 3:

{ displaystyle X = left {{ begin {matrix} 1 & { mbox {with}} { mbox {вероятность}} 1/3, 2 & { mbox {with}} { mbox {вероятность}} 1/3, 3 & { mbox {with}} { mbox {вероятность}} 1/3. end {matrix}} right.}

Вероятностная функция масс случайной величины Икс может быть изображен следующим гистограмма:

Ясно, что это не похоже на колоколообразную кривую нормального распределения. Сравните приведенное выше с изображениями ниже.

Сумма всех перестановок длины 2, выбранных из набора целых чисел 1, 2, 3

Вероятностная функция массы суммы двух членов

Теперь рассмотрим сумму двух независимых копий Икс:

{ Displaystyle left {{ begin {matrix} 1 + 1 & = & 2 1 + 2 & = & 3 1 + 3 & = & 4 2 + 1 & = & 3 2 + 2 & = & 4 2+ 3 & = & 5 3 + 1 & = & 4 3 + 2 & = & 5 3 + 3 & = & 6 end {matrix}} right } = left {{ begin {matrix} 2 & { mbox { с}} { mbox {вероятность}} 1/9 3 & { mbox {с}} { mbox {вероятность}} 2/9 4 & { mbox {с}} { mbox {вероятность}} 3/9 5 & { mbox {с}} { mbox {вероятность}} 2/9 6 & { mbox {с}} { mbox {вероятность}} 1/9 end {matrix}} right }}

Функцию массы вероятности этой суммы можно изобразить следующим образом:

Это все еще не очень похоже на колоколообразную кривую, но, как колоколообразная кривая и в отличие от вероятностной функции массы Икс сама по себе она выше посередине, чем в двух хвостах.

Сумма всех перестановок длины 3, выбранных из набора целых чисел 1, 2, 3

Вероятностная функция массы суммы трех членов

Теперь рассмотрим сумму три независимые копии этой случайной величины:

{ Displaystyle left {{ begin {matrix} 1 + 1 + 1 & = & 3 1 + 1 + 2 & = & 4 1 + 1 + 3 & = & 5 1 + 2 + 1 & = & 4 1 + 2 + 2 & = & 5 1 + 2 + 3 & = & 6 1 + 3 + 1 & = & 5 1 + 3 + 2 & = & 6 1 + 3 + 3 & = & 7 2 + 1 + 1 & = & 4 2 + 1 + 2 & = & 5 2 + 1 + 3 & = & 6 2 + 2 + 1 & = & 5 2 + 2 + 2 & = & 6 2 + 2 + 3 & = & 7 2+ 3 + 1 & = & 6 2 + 3 + 2 & = & 7 2 + 3 + 3 & = & 8 3 + 1 + 1 & = & 5 3 + 1 + 2 & = & 6 3 + 1 + 3 & = & 7 3 + 2 + 1 & = & 6 3 + 2 + 2 & = & 7 3 + 2 + 3 & = & 8 3 + 3 + 1 & = & 7 3 + 3 + 2 & = & 8 3 + 3 +3 & = & 9 end {matrix}} right } = left {{ begin {matrix} 3 & { mbox {with}} { mbox {вероятность}} 1/27 4 & { mbox {с}} { mbox {вероятность}} 3/27 5 & { mbox {с}} { mbox {вероятность}} 6/27 6 & { mbox {с}} { mbox {вероятность}} 7/27 7 & { mbox {с}} { mbox {вероятность}} 6/27 8 & { mbox {с}} { mbox {вероятность} } 3/27 9 & { mbox {with}} { mbox {вероятность}} 1/27 end {matrix}} right }}

Функцию массы вероятности этой суммы можно изобразить следующим образом:

Мало того, что в центре он больше, чем в хвостах, но по мере того, как каждый движется к центру от любого хвоста, наклон сначала увеличивается, а затем уменьшается, как и в случае колоколообразной кривой.

Степень его сходства с колоколообразной кривой можно количественно оценить следующим образом. Учитывать

Pr (Икс₁ + Икс₂ + Икс₃ ≤ 7) = 1/27 + 3/27 + 6/27 + 7/27 + 6/27 = 23/27 = 0.85185... .

Насколько это близко к тому, что нормальный приближение дадут? Нетрудно заметить, что ожидаемое значение Y = Икс₁ + Икс₂ + Икс₃ равно 6, а стандартное отклонение Y это квадратный корень из 2. С Y ≤ 7 (слабое неравенство) тогда и только тогда, когда Y <8 (строгое неравенство), воспользуемся исправление непрерывности и искать

{ displaystyle { mbox {Pr}} (Y leq 7.5) = { mbox {P}} left ({Y-6 over { sqrt {2}}} leq {7.5-6 over { sqrt {2}}} right) = { mbox {Pr}} (Z leq 1.0606602 dots) = 0.85558 dots}

куда Z имеет стандартное нормальное распределение. Разница между 0,85185 ... и 0,85558 ... кажется удивительно малой, если учесть, что число добавленных независимых случайных величин было всего три.

Вероятностная массовая функция суммы 1000 членов

На следующем изображении показан результат моделирования на основе примера, представленного на этой странице. Извлечение из равномерного распределения повторяется 1000 раз, и результаты суммируются.

Поскольку моделирование основано на Метод Монте-Карло, процесс повторяется 10 000 раз. Результаты показывают, что распределение суммы 1000 однородных экстракций очень хорошо напоминает колоколообразную кривую.

Navigation