WikiDer > Линия влияния
В инженерии линия влияния отображает изменение функции (например, сдвига в элементе конструкции) в определенной точке на луч или же ферма вызвано единичной нагрузкой, размещенной в любой точке конструкции.[1][2][3][4][5] Общие функции, изучаемые с помощью линий влияния, включают реакции (силы, которые должны прикладывать опоры конструкции, чтобы конструкция оставалась статичной), срезать, момент, и отклонение (Деформация).[6] Линии влияния важны при проектировании балок и ферм, используемых в мосты, подкрановые рельсы, конвейерные ленты, балки перекрытия и другие конструкции, по пролетам которых будут перемещаться нагрузки.[5] Линии влияния показывают, где нагрузка создаст максимальный эффект для любой из изученных функций.
Линии влияния обе скаляр и добавка.[5] Это означает, что их можно использовать, даже если прилагаемая нагрузка не является единичной нагрузкой или если приложено несколько нагрузок. Чтобы найти влияние любой неединичной нагрузки на конструкцию, результаты ординат, полученные по линии влияния, умножаются на величину действительной нагрузки, которая должна быть приложена. Можно масштабировать всю линию влияния или только максимальные и минимальные эффекты, испытываемые вдоль линии. Масштабированные максимум и минимум - это критические величины, на которые необходимо рассчитывать балку или ферму.
В случаях, когда могут действовать множественные нагрузки, линии влияния для отдельных нагрузок могут быть сложены вместе, чтобы получить общий эффект, ощущаемый конструкцией в данной точке. При сложении линий влияния необходимо включить соответствующие смещения из-за разнесения нагрузок по конструкции. Например, к конструкции прилагается груз грузовика. Задняя ось B находится на расстоянии трех футов от передней оси A, тогда эффект A на Икс футов вдоль конструкции необходимо добавить к эффекту B на (Икс - 3) ноги вдоль конструкции - не влияние B на Икс ноги по конструкции.
Многие нагрузки распределены, а не сосредоточены. Линии воздействия могут использоваться как с сосредоточенными, так и с распределенными нагрузками. При сосредоточенной (или точечной) нагрузке единичная точечная нагрузка перемещается по конструкции. Для распределенной нагрузки заданной ширины единично-распределенная нагрузка такой же ширины перемещается вдоль конструкции, отмечая, что, когда нагрузка приближается к концам и отодвигается от конструкции, только часть общей нагрузки воспринимается конструкцией. Эффект распределенной единичной нагрузки также может быть получен путем интегрирования линии влияния точечной нагрузки по соответствующей длине конструкций.
Линии Влияния определенных структур становятся механизмом, тогда как Линии Влияния неопределенных структур становятся просто определенными.[7]
Демонстрация теоремы Бетти
Линии влияния основаны на Теорема Бетти. Отсюда рассмотрим две системы внешних сил, и , каждый из которых связан с полем смещения, смещения которого, измеренные в точке приложения силы, представлены как и .
Считаем, что Система представляет собой действительные силы, приложенные к конструкции, которые находятся в равновесии. Считаем, что система образована единой силой, . Поле смещения связанный с этой силой, определяется снятием структурных ограничений, действующих в точке, где применяется и вызывает относительное единичное смещение, кинематически допустимое в отрицательном направлении, представленное как . Из Теорема Бетти, получаем следующий результат:
Концепция
При проектировании балки или фермы необходимо учитывать сценарии, вызывающие максимальные ожидаемые реакции, сдвиги и моменты внутри элементов конструкции, чтобы гарантировать, что ни один элемент не выйдет из строя в течение срока службы конструкции. При работе с мертвые нагрузки (нагрузки, которые никогда не перемещаются, например, вес самой конструкции), это относительно просто, потому что нагрузки легко прогнозировать и планировать. За живые нагрузки (любая нагрузка, которая перемещается в течение срока службы конструкции, например, мебель и люди), становится намного сложнее предсказать, где будут находиться нагрузки, а также насколько они будут сосредоточены или распределены в течение всего срока службы конструкции.
Линии влияния отображают реакцию балки или фермы при перемещении по ней единичной нагрузки. Линия влияния помогает проектировщикам найти, где разместить динамическую нагрузку, чтобы вычислить максимальную результирующую реакцию для каждой из следующих функций: реакции, сдвига или момента. Затем проектировщик может масштабировать линию влияния с учетом максимальной ожидаемой нагрузки, чтобы рассчитать максимальный отклик каждой функции, для которой должна быть спроектирована балка или ферма. Линии влияния также могут использоваться для определения откликов других функций (таких как прогиб или осевое сила) к приложенной единичной нагрузке, но такое использование линий влияния менее распространено.
Методы построения линий влияния
Для построения линии влияния используются три метода. Первый состоит в том, чтобы составить таблицу значений влияния для нескольких точек вдоль конструкции, а затем использовать эти точки для создания линии влияния.[5] Второй - определить уравнения линии влияния, которые применяются к конструкции, тем самым решая для всех точек вдоль линии влияния в терминах Икс, куда Икс - это количество футов от начала конструкции до точки приложения удельной нагрузки.[1][2][3][4][5] Третий метод называется Принцип Мюллера-Бреслау. Это создает качественный линия влияния.[1][2][5] Эта линия влияния по-прежнему предоставит проектировщику точное представление о том, где единичная нагрузка вызовет наибольший отклик функции в исследуемой точке, но ее нельзя использовать напрямую для расчета величины этого отклика, тогда как влияние линии, произведенные первыми двумя методами, могут.
Свести значения в таблицу
Чтобы свести в таблицу значения влияния по отношению к некоторой точке А на конструкции, необходимо разместить единичную нагрузку в различных точках конструкции. Статика используется для вычисления значения функции (реакции, сдвига или момента) в точке A. Обычно восходящая реакция считается положительной. Сдвигу и моментам присваиваются положительные или отрицательные значения в соответствии с теми же соглашениями, которые используются для диаграммы сдвига и момента.
Р. К. Хиббелер утверждает в своей книге Структурный анализ, «Все статически определенные балки будут иметь линии влияния, состоящие из отрезков прямых линий».[5] Следовательно, можно минимизировать количество вычислений, распознавая точки, которые вызовут изменение наклона линии влияния, и вычисляя значения только в этих точках. Наклон линии перегиба может изменяться на опорах, средних пролетах и стыках.
Линия влияния для данной функции, такой как реакция, осевая сила, поперечная сила или изгибающий момент, представляет собой график, который показывает изменение этой функции в любой заданной точке конструкции из-за приложения единичной нагрузки в любой точке. точка на конструкции.
Линия влияния для функции отличается от диаграммы сдвига, осевого или изгибающего момента. Линии влияния могут быть созданы путем независимого приложения единичной нагрузки в нескольких точках конструкции и определения значения функции, обусловленной этой нагрузкой, то есть сдвига, осевого усилия и момента в желаемом месте. Затем рассчитанные значения для каждой функции наносятся на график в том месте, где была приложена нагрузка, а затем соединяются вместе, чтобы создать линию влияния для функции.
После того, как значения влияния занесены в таблицу, можно провести линию влияния для функции в точке A в терминах Икс. Сначала необходимо найти табличные значения. Для участков между точками в таблице требуется интерполяция. Поэтому для соединения точек можно провести прямые линии. Как только это будет сделано, линия влияния завершится.
Уравнения линии влияния
Можно создать уравнения, определяющие линию влияния на всем пролете конструкции. Это делается путем решения реакции, сдвига или момента в точке A, вызванной единичной нагрузкой, помещенной в Икс футов вдоль конструкции вместо определенного расстояния. Этот метод аналогичен методу табличных значений, но вместо получения числового решения результатом является уравнение в терминах Икс.[5]
Важно понимать, где изменяется наклон линии влияния для этого метода, потому что уравнение линии влияния будет изменяться для каждого линейного участка линии влияния. Следовательно, полное уравнение представляет собой кусочно-линейная функция с отдельным уравнением линии влияния для каждого линейного участка линии влияния.[5]
Принцип Мюллера-Бреслау
Согласно www.public.iastate.edu, «Принцип Мюллера-Бреслау можно использовать для рисования качественный линии влияния, которые прямо пропорциональны фактической линии влияния ».[2] Вместо того, чтобы перемещать единичный груз вдоль балки, принцип Мюллера-Бреслау находит отклоненную форму балки, вызванную первым выпуском балки в исследуемой точке, а затем применением исследуемой функции (реакции, сдвига или момента) к этот момент. Принцип гласит, что линия влияния функции будет иметь масштабированную форму, которая будет такой же, как форма отклонения луча, когда на луч воздействует функция.
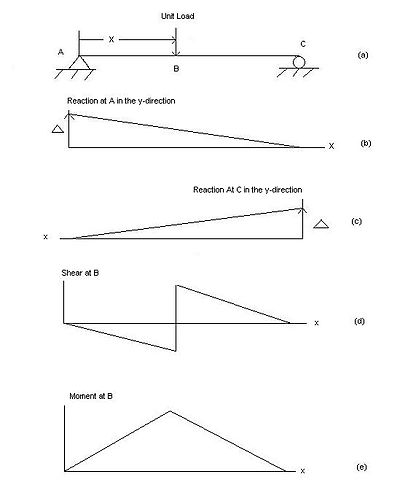
Чтобы понять, как луч отклоняется под действием функции, необходимо исключить способность луча сопротивляться этой функции. Ниже приведены объяснения того, как найти линии влияния жесткой балки с простой опорой (например, показанной на рисунке 1).
- При определении реакции, вызванной опорой, опора заменяется роликом, который не может сопротивляться вертикальной реакции.[2][5] Затем применяется восходящая (положительная) реакция к точке, где была поддержка. Поскольку опора была удалена, балка будет вращаться вверх, и, поскольку балка жесткая, образуется треугольник с точкой на второй опоре. Если балка выступает за пределы второй опоры как консоль, подобный треугольник будет сформирован ниже положения консолей. Это означает, что линия влияния реакции будет прямой наклонной линией с нулевым значением в месте расположения второй поддержки.
- При определении сдвига, вызванного в некоторой точке B вдоль балки, балку необходимо разрезать, и в точку B необходимо вставить роликовый направляющий (который способен выдерживать моменты, но не сдвиг).[2][5] Затем, приложив к этой точке положительный сдвиг, можно увидеть, что левая сторона повернется вниз, а правая - вверх. Это создает прерывистую линию влияния, которая достигает нуля на опорах и имеет одинаковый наклон по обе стороны от разрыва. Если точка B находится на опоре, то отклонение между точкой B и любыми другими опорами по-прежнему будет создавать треугольник, но если балка консольная, тогда вся консольная сторона будет перемещаться вверх или вниз, образуя прямоугольник.
- При определении момента, вызванного в некоторой точке B вдоль балки, шарнир будет помещен в точку B, освобождая его на моменты, но сопротивляясь сдвигу.[2][5] Затем, когда в точке B будет установлен положительный момент, обе стороны балки повернутся вверх. Это создаст непрерывную линию влияния, но наклоны будут равными и противоположными по обе стороны от петли в точке B. Поскольку балка просто поддерживается, ее концевые опоры (штифты) не могут сопротивляться моменту; следовательно, можно заметить, что опоры никогда не будут испытывать моменты в статической ситуации, независимо от того, где находится нагрузка.
Принцип Мюллера-Бреслау может создавать только качественные линии влияния.[2][5] Это означает, что инженеры могут использовать его, чтобы определить, где разместить нагрузку, чтобы получить максимум функции, но величину этого максимума нельзя рассчитать по линии влияния. Вместо этого инженер должен использовать статику для определения значения функции в этом случае нагрузки.
Альтернативные варианты загрузки
Множественные нагрузки
Самый простой вариант нагружения - это одноточечная нагрузка, но линии влияния также могут использоваться для определения реакции на множественные нагрузки и распределенные нагрузки. Иногда известно, что на некотором фиксированном расстоянии друг от друга будут возникать множественные нагрузки. Например, на мосту колеса легковых или грузовых автомобилей создают точечные нагрузки, действующие на относительно стандартных расстояниях.
Чтобы вычислить реакцию функции на все эти точечные нагрузки с использованием линии влияния, результаты, полученные с линией влияния, можно масштабировать для каждой нагрузки, а затем масштабированные величины можно суммировать, чтобы найти общий отклик, который должна выдержать конструкция.[5] Точечные нагрузки сами по себе могут иметь разные величины, но даже если они прилагают одинаковую силу к конструкции, их необходимо масштабировать отдельно, поскольку они действуют на разных расстояниях вдоль конструкции. Например, если колеса автомобиля находятся на расстоянии 10 футов друг от друга, тогда, когда первый набор находится на расстоянии 13 футов от моста, второй набор будет только на 3 фута от моста. Если первая пара колес находится на 7 футов от моста, вторая пара еще не достигла моста, и поэтому только первая пара создает нагрузку на мост.
Кроме того, если между двумя грузами одна из нагрузок более тяжелая, нагрузки должны быть проверены в обоих порядках загрузки (большая нагрузка справа и большая нагрузка слева), чтобы убедиться, что найдена максимальная нагрузка. Если имеется три и более нагрузок, то количество случаев, подлежащих рассмотрению, увеличивается.
Распределенные нагрузки
Многие нагрузки не действуют как точечные, а действуют на увеличенной длине или площади как распределенные нагрузки. Например, трактор с непрерывные дорожки приложит нагрузку, распределенную по длине каждой дорожки.
Чтобы найти влияние распределенной нагрузки, проектировщик может интегрировать линию влияния, найденную с помощью точечной нагрузки, на затронутом расстоянии конструкции.[5] Например, если путь длиной три фута проходит между 5 и 8 футами вдоль балки, линия воздействия этой балки должна быть интегрирована между 5 и 8 футами. Интеграция линии влияния дает эффект, который ощущался бы, если бы распределенная нагрузка имела единичную величину. Следовательно, после интеграции разработчик должен по-прежнему масштабировать результаты, чтобы получить фактический эффект распределенной нагрузки.
Неопределенные структуры
Хотя линии влияния статически определенных структур (как упоминалось выше) состоят из отрезков прямых линий, то же самое не относится к неопределенным структурам. Неопределенные конструкции не считаются жесткими; поэтому нарисованные для них линии влияния будут не прямыми, а скорее кривыми. Вышеупомянутые методы все еще можно использовать для определения линий влияния на структуру, но работа становится намного более сложной, поскольку необходимо учитывать свойства самой балки.
Смотрите также
Рекомендации
- ^ а б c Харагпур. "Structural Analysis.pdf, Версия 2 CE IIT" В архиве 2010-08-19 в Wayback Machine. 7 августа 2008 г. Проверено 26 ноября 2010 г.
- ^ а б c d е ж грамм час Доктор Фаноус, Фуад. «Вводные задачи структурного анализа: линии влияния». 20 апреля 2000 г. Проверено 26 ноября 2010 г.
- ^ а б «Метод анализа линии влияния». Конструктор. 10 февраля 2010 г. Проверено 26 ноября 2010 г.
- ^ а б «Структурный анализ: линии влияния». Коалиция Фонда. 2 декабря 2010 г. Проверено 26 ноября 2010 г.
- ^ а б c d е ж грамм час я j k л м п о Hibbeler, R.C. (2009). Структурный анализ (седьмое издание). Пирсон Прентис Холл, Нью-Джерси. ISBN 0-13-602060-7.
- ^ Зейнали, Яша (декабрь 2017). «Структура для оценки жесткости на изгиб в балках Эйлера-Бернулли с использованием линий воздействия деформации». Инфраструктуры. 2 (4): 23. Дои:10.3390 / инфраструктуры2040023.
- ^ "Линии влияния | Обзор структурного анализа". www.mathalino.com. Получено 2019-12-25.






