WikiDer > Ферма

А ферма представляет собой сборку балок или других элементов, которая создает жесткую конструкцию.[1]
В технике ферма - это структура это «состоит только из двух силовых элементов, где элементы организованы так, что сборка в целом ведет себя как единый объект».[2] «Элемент с двумя силами» - это структурный элемент, в котором сила приложена только к двум точкам. Хотя это строгое определение позволяет элементам иметь любую форму, соединенную в любой устойчивой конфигурации, фермы обычно содержат пять или более треугольных блоков, построенных из прямых элементов, концы которых соединены в соединениях, называемых узлы.
В этом типичном контексте считается, что внешние силы и реакции на эти силы действуют только в узлах и приводят к силам в элементах, которые либо растяжение или сжимающий. Для обычных членов моменты (крутящие моменты) явно исключаются потому и только потому, что все соединения в ферме рассматриваются как революционеры, поскольку это необходимо для того, чтобы звенья были двусоставными.
Плоская ферма - это ферма, в которой все элементы и узлы лежат в двухмерной плоскости, а в пространственной ферме элементы и узлы простираются в три измерения. Верхние балки фермы называются верхние аккорды и обычно находятся в сжатие, нижние балки называются нижние пояса, и обычно находятся в напряжение. Внутренние балки называются сети, а области внутри паутины называются панели,[3] или из графической статики (см. Диаграмма Кремоны) полигоны.[4]
Этимология
Ферма происходит от Старофранцузский слово трусс, примерно с 1200, что означает «собрание вещей, связанных вместе».[5][6] Период, термин ферма часто использовался для описания любого собрания членов, такого как крук Рамка[7][8] или пара стропил.[9][10] Одно из инженерных определений таково: «Ферма - это каркас из одной плоскости, состоящий из отдельных структурных элементов [sic], соединенных на концах и образующих серию треугольников [sic] для охвата большого расстояния».[11]
Характеристики
Ферма обычно состоит из прямых (но не обязательно) прямых элементов, соединенных в соединениях, традиционно называемых панели точек. Фермы обычно (но не обязательно[12]) состоит из треугольников из-за структурной устойчивости этой формы и конструкции. Треугольник - простейшая геометрическая фигура, которая не меняет форму при фиксированной длине сторон.[13] Для сравнения, как углы, так и длина четырехгранной фигуры должны быть фиксированными, чтобы она сохраняла свою форму. Соединение, на которое должна опираться ферма, обычно называют точкой Мюнтера.[нужна цитата]
Простая ферма

Самая простая форма фермы - это один единственный треугольник. Этот тип фермы встречается в обрамленный крыша, состоящая из стропила и потолок балка,[14] и в других механических конструкциях, таких как велосипеды и самолет. Из-за устойчивости этой формы и методов анализа, используемых для расчета сил внутри нее, ферма, полностью состоящая из треугольников, известна как простая ферма.[15] Однако простая ферма часто определяется более строго, требуя, чтобы она могла быть построена путем последовательного добавления пар элементов, каждая из которых соединена с двумя существующими соединениями и друг с другом, чтобы сформировать новое соединение, и это определение не требует простой фермы. состоять только из треугольников.[12] Традиционная рама велосипеда ромбовидной формы, в которой используются два соединенных треугольника, является примером простой фермы.[16]
Планарная ферма
Плоская ферма лежит в единой самолет.[15] Плоские фермы обычно используются параллельно для образования крыш и мостов.[17]
Глубина фермы или высота между верхними и нижними поясами - вот что делает ее эффективной структурной формой. Твердый ферма или луч равной прочности будет иметь значительный вес и стоимость материала по сравнению с фермой. Для данного размах, более глубокая ферма потребует меньше материала в поясах и больше материала по вертикали и диагоналям. Оптимальная глубина фермы максимизирует эффективность.[18]
Ферма космического каркаса
А космический каркас Ферма - это трехмерный каркас из элементов, закрепленных на концах. А тетраэдр shape - это простейшая пространственная ферма, состоящая из шести элементов, которые встречаются в четырех местах соединения.[15] Большие плоские конструкции могут быть составлены из тетраэдров с общими краями, и они также используются в базовых конструкциях больших отдельно стоящих опор линий электропередач.
Эта электрический пилон представляет собой трехмерную ферменную конструкцию
Типы
- Дополнительные типы ферм см. типы ферм, используемые в мостах.

Существует два основных типа фермы:
- Скатная ферма, или обычная ферма, характеризуется своей треугольной формой. Чаще всего используется для строительства крыш. Некоторые общие фермы названы в соответствии с их «конфигурацией сети». Размер пояса и конфигурация полотна определяются пролетом, нагрузкой и расстоянием.
- Ферма с параллельными поясами, или плоская ферма, получила свое название от параллельных верхних и нижних поясов. Его часто используют для устройства полов.
Комбинация этих двух элементов представляет собой усеченную ферму, используемую в бедро конструкция крыши. Деревянная ферма, соединенная металлическими пластинами, представляет собой ферму крыши или пола, деревянные элементы которой соединены с металлические соединительные пластины.
Ферма Уоррена
![]() Элементы фермы образуют серию равносторонних треугольников, чередующихся вверх и вниз. Основная статья: Ферма Уоррена
Элементы фермы образуют серию равносторонних треугольников, чередующихся вверх и вниз. Основная статья: Ферма Уоррена
Октет фермы
Элементы фермы состоят из всех равнозначных равносторонних треугольников. Минимальный состав - два правильных тетраэдра вместе с октаэдром. Они заполняют трехмерное пространство в самых разных конфигурациях.
Ферма Пратта
![]() Ферма Pratt была запатентована в 1844 году двумя Бостон инженеры-железнодорожники,[19] Калеб Пратт и его сын Томас Уиллис Пратт.[20] В конструкции используются вертикальные элементы для сжатие и диагональные элементы для ответа на напряжение. Конструкция фермы Пратта оставалась популярной, поскольку проектировщики мостов перешли с дерева на железо и с железа на сталь.[21] Эта постоянная популярность фермы Pratt, вероятно, связана с тем, что конфигурация элементов означает, что более длинные диагональные элементы находятся в напряжении только для воздействия гравитационной нагрузки. Это позволяет использовать эти элементы более эффективно, поскольку эффекты гибкости, связанные с коробление при сжимающих нагрузках (которые усугубляются длиной элемента) обычно не влияет на конструкцию. Следовательно, для данной плоской фермы с фиксированной глубиной конфигурация Пратта обычно наиболее эффективна при статической вертикальной нагрузке.
Ферма Pratt была запатентована в 1844 году двумя Бостон инженеры-железнодорожники,[19] Калеб Пратт и его сын Томас Уиллис Пратт.[20] В конструкции используются вертикальные элементы для сжатие и диагональные элементы для ответа на напряжение. Конструкция фермы Пратта оставалась популярной, поскольку проектировщики мостов перешли с дерева на железо и с железа на сталь.[21] Эта постоянная популярность фермы Pratt, вероятно, связана с тем, что конфигурация элементов означает, что более длинные диагональные элементы находятся в напряжении только для воздействия гравитационной нагрузки. Это позволяет использовать эти элементы более эффективно, поскольку эффекты гибкости, связанные с коробление при сжимающих нагрузках (которые усугубляются длиной элемента) обычно не влияет на конструкцию. Следовательно, для данной плоской фермы с фиксированной глубиной конфигурация Пратта обычно наиболее эффективна при статической вертикальной нагрузке.
В Южно-Тихоокеанская железная дорога мост в Темпе, Аризона представляет собой ферменный мост длиной 393 метра (1291 фут), построенный в 1912 году.[22][23] Конструкция состоит из девяти пролетов фермы Pratt разной длины. Мост все еще используется.
В Райт Флаер в конструкции крыла использовалась ферма Pratt, поскольку минимизация длины сжатых элементов позволила снизить аэродинамическое сопротивление.[24]
Ферма тетива
Названные по форме, фермы тетивы впервые использовались для арочных ферменные мосты, часто путают с арочные мосты.
Тысячи тетивных ферм использовались во время Вторая Мировая Война для поддержки изогнутых крыш авиационных ангаров и других военных зданий. Существует множество вариантов расположения элементов, соединяющих узлы верхней дуги с узлами нижней прямой последовательности элементов, от почти равнобедренных треугольников до варианта фермы Пратта.
Ферма столба короля
Один из самых простых стилей фермы для реализации, центральная стойка состоит из двух наклонных опор, опирающихся на общую вертикальную опору.
Ферма столба королевы, иногда королевский столб или Queenspost, похожа на ферму королевского столба тем, что внешние опоры расположены под углом к центру конструкции. Основное отличие - это горизонтальное расширение в центре, которое опирается на луч действие, обеспечивающее механическую стабильность. Этот стиль фермы подходит только для относительно коротких пролетов.[25]
Линзовидная ферма
Линзовидные фермы, запатентованные в 1878 году Уильямом Дугласом (хотя Безгорный мост 1823 г. был первым типом), имели верхние и нижние пояса фермы арочные, образующие линзовидную форму. А линзовидный мост пони фермы представляет собой конструкцию моста, включающую линзовидную ферму, проходящую над и под полотном дороги.
Решетчатая ферма города
Американский архитектор Итиэль спроектировал городскую решетчатую ферму в качестве альтернативы мостам из тяжелой древесины. Его дизайн, запатентованный в 1820 и 1835 годах использует простые в обращении доски, расположенные по диагонали с короткими промежутками между ними, чтобы сформировать решетка.
Ферма Vierendeel

Ферма Виренделя - это конструкция, в которой элементы не триангулированы, а образуют прямоугольные отверстия, и представляет собой Рамка с фиксированными соединениями, способными передавать и сопротивляться изгибающие моменты. Таким образом, это не соответствует строгому определению фермы (поскольку она содержит элементы, не обладающие двумя силами): обычные фермы включают элементы, которые, как обычно предполагается, имеют шарнирные соединения, что подразумевает отсутствие моментов на соединенных концах. Этот стиль конструкции был назван в честь бельгийского инженера. Артур Вирендил,[26] который разработал конструкцию в 1896 году. Его использование для мостов редко из-за более высокой стоимости по сравнению с триангулированной фермой.
Полезность этого типа конструкции в зданиях заключается в том, что большая часть внешней оболочки остается незагороженной и может использоваться для окна и дверные проемы. В некоторых приложениях это предпочтительнее, чем система с подкосами, при которой некоторые области будут закрыты диагональными скобами.
Статика

Ферма, которая, как предполагается, содержит элементы, которые соединяются с помощью шарнирных соединений и которая поддерживается с обоих концов с помощью шарнирных соединений или роликов, описывается как статически определен. Законы Ньютона применяются к конструкции в целом, а также к каждому узлу или стыку. Чтобы любой узел, который может подвергаться внешней нагрузке или силе, оставался статичным в пространстве, должны выполняться следующие условия: суммы всех (горизонтальных и вертикальных) сил, а также всех моментов, действующих вокруг узла, равны нулю. Анализ этих условий в каждом узле дает величину сил сжатия или растяжения.
Фермы, которые поддерживаются более чем в двух позициях, считаются статически неопределенный, и применения только законов Ньютона недостаточно для определения сил стержня.
Чтобы ферма с элементами, соединенными штифтами, была устойчивой, не обязательно, чтобы она полностью состояла из треугольников.[12] С математической точки зрения имеем следующее необходимое условие для стабильность простой фермы:
где м - общее количество элементов фермы, j общее количество стыков и р - количество реакций (обычно равное 3) в двумерной структуре.
Когда , ферма называется статически определен, поскольку (м+3) внутренние силы стержня и опорные реакции могут быть полностью определены 2j равновесие уравнения, как только мы узнаем внешние грузы и геометрия фермы. При определенном количестве соединений это минимальное количество стержней в том смысле, что если какой-либо элемент вынимается (или выходит из строя), то ферма в целом выходит из строя. Хотя соотношение (а) необходимо, его недостаточно для устойчивости, которая также зависит от геометрии фермы, условий опоры и несущей способности элементов.
Некоторые конструкции построены с большим, чем это минимальное количество элементов фермы. Эти структуры могут выжить даже тогда, когда некоторые из членов терпят неудачу. Их силы на членах зависят от относительной жесткость членов, в дополнение к описанному состоянию равновесия.
Анализ
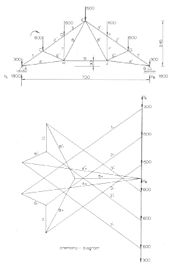
Поскольку силы в каждой из двух основных балок по существу плоские, ферма обычно моделируется как двухмерный плоский каркас. Однако при наличии значительных сил вне плоскости конструкция должна быть смоделирована как трехмерное пространство.
При расчете ферм часто предполагается, что нагрузки прикладываются только к соединениям, а не к промежуточным точкам вдоль элементов. Вес элементов часто незначителен по сравнению с приложенными нагрузками и поэтому часто не учитывается; в качестве альтернативы, половина веса каждого элемента может быть приложена к его двум концевым соединениям. При условии, что члены длинные и стройные, моменты передаваемые через суставы незначительны, и их можно рассматривать как "петли"или" шарнирные соединения ".
При этих упрощающих предположениях каждый элемент фермы затем подвергается чистому воздействию. сжатие или чистый напряжение силы - сдвиг, изгибающий момент и другие более сложные подчеркивает все практически равны нулю. Фермы физически прочнее, чем другие способы расположения элементов конструкции, потому что почти каждый материал может выдерживать гораздо большую нагрузку при растяжении или сжатии, чем при сдвиге, изгибе, скручивании или других видах сил.
Эти упрощения упрощают анализ ферм. Структурный анализ ферм любого типа могут быть легко выполнены с использованием матричного метода, такого как метод прямой жесткости, то метод гибкости, или заключительный элемент метод.
Силы в членах
Проиллюстрирован простой, статически определен плоская ферма с 9 шарнирами и (2 x 9) - 3 = 15 стержнями. Внешние нагрузки сосредоточены во внешних шарнирах. Поскольку это симметричный фермы с симметричными вертикальными нагрузками, реактивные силы в точках A и B равны вертикальным, равны и составляют половину общей нагрузки.
внутренний силы в элементах фермы можно рассчитать различными способами, в том числе графическими методами:
- Диаграмма Кремоны
- Диаграмма Калмана
- Аналитический метод Риттера (метод секций)
Дизайн участников
Ферму можно рассматривать как луч где полотно состоит из ряда отдельных элементов вместо непрерывной пластины. В ферме нижний горизонтальный элемент ( нижний пояс) и верхний горизонтальный элемент ( верхний аккорд) нести напряжение и сжатие, выполняя ту же функцию, что и фланцы из Двутавровая балка. Какой пояс несет растяжение, а какой - сжатие, зависит от общего направления изгиб. В ферме, изображенной справа вверху, нижний пояс находится в растяжении, а верхний пояс в сжатом состоянии.
Диагональные и вертикальные элементы образуют ферменная ткань, и нести напряжение сдвига. По отдельности они также находятся в состоянии растяжения и сжатия, точное расположение сил зависит от типа фермы и, опять же, от направления изгиба. В ферме, показанной справа вверху, вертикальные элементы находятся в растяжении, а диагонали - в сжатом состоянии.
В дополнение к статическим силам, элементы выполняют дополнительные функции стабилизации друг друга, предотвращая коробление. На изображении рядом с верхним поясом искривление предотвращается за счет наличия связей и жесткости элементов перемычки.
Включение показанных элементов - это в основном инженерное решение, основанное на экономических соображениях и являющееся балансом между затратами на сырье, изготовление за пределами площадки, транспортировку компонентов, монтаж на месте, доступность оборудования и стоимость рабочей силы. В других случаях внешний вид конструкции может иметь большее значение и, таким образом, влиять на проектные решения, выходящие за рамки чисто экономических вопросов. Современные материалы, такие как предварительно напряженный бетон и методы изготовления, такие как автоматизированные сварка, существенно повлияли на дизайн современных мосты.
После того, как сила, действующая на каждый элемент, известна, следующим шагом будет определение поперечное сечение отдельных элементов фермы. Для стержней, находящихся под напряжением, площадь поперечного сечения А можно найти с помощью А = F × γ / σу, где F сила в стержне, γ - коэффициент безопасности (обычно 1.05, но в зависимости от строительные нормы) и σу это доход предел прочности используемой стали.
Элементы, подвергающиеся сжатию, также должны быть спроектированы таким образом, чтобы не допускать коробления.
Вес элемента фермы напрямую зависит от его поперечного сечения - этот вес частично определяет, насколько прочными должны быть другие элементы фермы. Чтобы дать одному члену большее поперечное сечение, чем на предыдущей итерации, необходимо предоставить другим членам также большее поперечное сечение, чтобы выдержать больший вес первого члена - нужно пройти еще одну итерацию, чтобы точно определить, насколько больше нужно другим членам. быть. Иногда проектировщик проходит несколько итераций процесса проектирования, чтобы найти «правильное» поперечное сечение для каждого элемента. С другой стороны, уменьшение размера одного члена из предыдущей итерации просто приводит к тому, что другие члены имеют больший (и более дорогой) коэффициент безопасности, чем это технически необходимо, но не требовать еще одна итерация, чтобы найти сборную ферму.
Влияние веса отдельных элементов фермы в большой ферме, такой как мост, обычно незначительно по сравнению с силой внешних нагрузок.
Дизайн стыков
После определения минимального поперечного сечения элементов последним шагом в проектировании фермы будет детализация болтовые соединения, например, касающееся напряжения сдвига болтовых соединений, используемых в соединениях. Исходя из требований проекта, внутренние соединения (стыки) фермы могут быть жесткими, полужесткими или шарнирными. Жесткие соединения могут допускать передачу изгибающих моментов, что приводит к развитию вторичных изгибающих моментов в элементах.
Приложения
Пост-каркасные конструкции
Соединения компонентов имеют решающее значение для структурной целостности каркасной системы. В зданиях с большими деревянными фермами с чистым пролетом наиболее важными соединениями являются соединения между фермой и ее опорами. В дополнение к силам силы тяжести (так называемым нагрузкам на подшипники) эти соединения должны противостоять поперечным силам, действующим перпендикулярно плоскости фермы, и подъемным силам, создаваемым ветром. В зависимости от общей конструкции здания могут потребоваться соединения для передачи изгибающего момента.
Деревянные стойки позволяют создавать прочные, прямые и недорогие соединения между большими фермами и стенами. Точные детали соединений между стойками и фермами варьируются от дизайнера к проектировщику и могут зависеть от типа стойки. Столбы из массивной древесины и клееного бруса обычно имеют выемки для образования несущей поверхности фермы. Ферма опирается на пазы и прикручивается болтами. Может быть добавлена специальная пластина / кронштейн для увеличения возможностей передачи нагрузки соединения. С механически ламинированными стойками ферма может опираться на укороченный внешний слой или укороченный внутренний слой. В более позднем сценарии болты подвергаются двойному сдвигу, что обеспечивает очень эффективное соединение.
Галерея
В Башня Гонконгского банка Китая имеет видимую снаружи стропильную конструкцию
В Главное здание HSBC, Гонконг имеет видимую снаружи стропильную конструкцию
Опорная конструкция под Оклендский мост через гавань
В Оклендский мост через гавань видно из Остров Сторожа к западу
Маленький пояс: ферма мост в Дания
Ферма крыши в пристройке Cluny Abbey, Франция
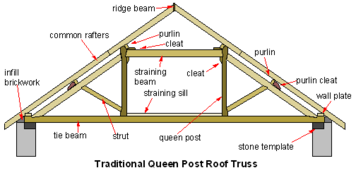
Раздел через пост королевы деревянная ферма крыши
Космическая ферма, несущая пол в Торговый центр Woodlands
Современный временный мост из Бейли-Бридж ферменные панели в Монреаль Квебек
Трехмерная ферменная конструкция от Юник Ротарекс®
Смотрите также
- Решетчатая башня
- Тесселяции Андреини, всего 28 способов заполнить трехмерное пространство фермами, имеющими идентичный суставы везде
- Коричневая ферма
- Геодезический купол, ферма в форме шара
- Строительная механика
- Ферма Серрурье, форма фермы, используемая для телескопов
- Стресс:
- Конструкционная сталь
- Ферма Тенсегрити, ферма, в которой ни один элемент сжатия не касается другого элемента сжатия
- Анкерный стержень, а гитара часть
использованная литература
- ^ «Определение ФЕРМЫ».
- ^ Плеша, Майкл Э .; Gray, Gary L .; Костанцо, Франческо (2013). Инженерная механика: статика (2-е изд.). Нью-Йорк: McGraw-Hill Companies Inc., стр. 364–407. ISBN 978-0-07-338029-2.
- ^ Чинг, Фрэнк. Визуальный словарь архитектуры. 2-е изд. Хобокен, Нью-Джерси: Wiley, 2012. 277. Print. ISBN 9780470648858
- ^ Боу Р. Х. Экономика строительства применительно к каркасным конструкциям. Спон, Лондон, 1873 г.
- ^ Рейф, Ф., etymonline.com (1965).
- ^ Оксфордский словарь английского языка
- ^ Благородный, Аллен Джордж. Традиционные здания - глобальный обзор структурных форм и культурных функций. Лондон: И. Тавры; 2007. 115. ISBN 1845113055
- ^ Дэвис, Николас и Эркки Йокиниеми. Словарь по архитектуре и строительству. Амстердам: Elsevier / Architectural Press, 2008. 394. ISBN 0750685026
- ^ Дэвис, Николас и Эркки Йокиниеми. Карманный иллюстрированный словарь архитектора. Оксфорд: Architectural Press, 2011. 121. ISBN 0080965377
- ^ Крабб, Джордж. Универсальный технологический словарь или знакомое объяснение терминов, используемых во всех искусствах и науках ... », том 1, Лондон: 1823 г. Пары.
- ^ Шекхар, Р. К. Чандра. Академический словарь гражданского строительства. Дели: Isha Books, 2005. 431. ISBN 8182051908
- ^ а б c Пиво, Ферд; Джонстон, Расс (2013). Векторная механика для инженеров: статика (10-е изд.). Нью-Йорк, штат Нью-Йорк: Макгроу-Хилл. С. 285–313. ISBN 978-0-07-740228-0.
- ^ Рикер, Натан Клиффорд (1912) [1912]. Удовольствие от проектирования и строительства крыш. Нью-Йорк: J. Wiley & Sons. п.12. Получено 2008-08-15.
- ^ Магиннис, Оуэн Бернард (1903). Каркас крыши - это просто (2-е изд.). Нью-Йорк: Промышленная издательская компания. п.9. Получено 2008-08-16.
- ^ а б c Хиббелер, Рассел Чарльз (1983) [1974]. Инженерная механика-статика (3-е изд.). Нью-Йорк: Macmillan Publishing Co., Inc., стр. 199–224. ISBN 0-02-354310-8.
- ^ Вингертер Р., Лебосьер П., МЭ 354, Лаборатория механики материалов: конструкции, Вашингтонский университет (февраль 2004 г.), стр.1.
- ^ Люблинер, Иаков; Пападопулос, Панайотис (2016-10-23). Введение в механику твердого тела: комплексный подход. Springer. ISBN 9783319188782.
- ^ Мерриман, Мэнсфилд (1912) [192]. Карманный справочник американских инженеров-строителей. Нью-Йорк: J. Wiley & Sons. п. 785. Получено 2008-08-16.
Экономическая глубина фермы - это то, что делает материал моста минимальным.
- ^ Бетанга мост на Офис наследия Нового Южного Уэльса; получено 6 февраля 2008 г.
- ^ Краткая история крытых мостов в Теннесси на Департамент транспорта Теннесси; получено 6 февраля 2008 г.
- ^ Ферма Пратта В архиве 2008-05-28 на Wayback Machine любезно предоставлено Департамент транспорта Мэриленда; получено 6 февраля 2008 г.
- ^ "1. Южно-тихоокеанский железнодорожный мост, мост Эш-авеню и мост Милл-авеню со стороны Темпе-Бьютта, смотрящего на северо-запад. - Восточный железнодорожный мост Аризоны, перемычка Солт-Ривер, Темпе, округ Марикопа, Аризона". Библиотека Конгресса, Вашингтон, округ Колумбия 20540 США. Получено 26 марта 2020.
- ^ Обзор исторической собственности Темпе В архиве 2007-11-10 на Wayback Machine на Исторический музей Темпе; получено 6 февраля 2008 г.
- ^ Дарио Гаспарини, Университет Кейс Вестерн Резерв. Братья Райт и ферма Пратта, слайды презентации
- ^ Типы ферм крытого моста В архиве 2008-05-12 на Wayback Machine
- ^ Vierendeel Bruggen
внешние ссылки
| Викискладе есть медиафайлы по теме фермы. |