WikiDer > Инверсия (дискретная математика)

Перестановка с выделенной одной из инверсий

Его можно обозначить парой мест (2, 4) или парой элементов (5, 2).

В Информатика и дискретная математика, последовательность имеет инверсия где два его элемента находятся вне их естественного порядок.

Определения

Инверсия

Позволять ${displaystyle pi}$ быть перестановка. Если ${displaystyle i$ и ${displaystyle pi (i)> pi (j)}$, либо пара мест ${displaystyle (i, j)}$^[1][2] или пара элементов ${displaystyle {igl (} пи (я), пи (дж) {игр)}}$^[3][4][5] называется инверсия из ${displaystyle pi}$.

Инверсия обычно определяется для перестановок, но также может быть определена для последовательностей:
Позволять ${displaystyle S}$ быть последовательность (или мультимножество перестановка^[6]). Если ${displaystyle i$ и ${displaystyle S (i)> S (j)}$, либо пара мест ${displaystyle (i, j)}$^[6][7] или пара элементов ${displaystyle {igl (} S (i), S (j) {igr)}}$^[8] называется инверсией ${displaystyle S}$.

Для последовательностей инверсии согласно определению на основе элементов не уникальны, потому что разные пары мест могут иметь одну и ту же пару значений.

В набор инверсии - это множество всех инверсий. Множество инверсии перестановки согласно определению на основе места - это то, что обратный набор инверсии перестановки в соответствии с определением на основе элементов, и наоборот,^[9] просто при обмене элементами пар.

Номер инверсии

В номер инверсии - мощность множества инверсии. Это общепринятая мера сортировки перестановки.^[5] или последовательность.^[8]

Это количество пересечений на стрелочной диаграмме перестановки,^[9] его Кендалл тау расстояние от тождественной перестановки и суммы каждого из векторов, связанных с инверсией, определенных ниже.

Не имеет значения, используется ли определение инверсии по месту или по элементам для определения числа инверсии, потому что перестановка и ее инверсия имеют одинаковое количество инверсий.

Другие меры (предварительной) сортировки включают минимальное количество элементов, которые могут быть удалены из последовательности, чтобы получить полностью отсортированную последовательность, количество и длину отсортированных "прогонов" в последовательности, правило Спирмена (сумма расстояний каждого элемент от его отсортированной позиции), и наименьшее количество обменов, необходимых для сортировки последовательности.^[10] Стандарт сортировка сравнения алгоритмы могут быть адаптированы для вычисления числа инверсии во времени O (п журнал п).^[11]

Инверсия связанных векторов

Используются три похожих вектора, которые конденсируют инверсии перестановки в вектор, который однозначно определяет ее. Их часто называют вектор инверсии или Код Лемера. (Список источников найден Вот.)

В этой статье используется термин вектор инверсии (${displaystyle v}$) любить Вольфрам.^[12] Остальные два вектора иногда называют осталось и правый вектор инверсии, но во избежание путаницы с вектором инверсии в этой статье они называются счетчик левой инверсии (${displaystyle l}$) и счетчик правых инверсий (${displaystyle r}$). Интерпретируется как факториальное число счетчик левой инверсии дает перестановки, обратные колексикографическим,^[13] а правильный счет инверсии дает лексикографический указатель.

Диаграмма Роте

Вектор инверсии ${displaystyle v}$:
С на основе элементов определение ${displaystyle v (i)}$ - количество инверсий, меньше (правый) компонент ${displaystyle i}$.^[3]

${displaystyle v (i)}$ это количество элементов в ${displaystyle pi}$ лучше чем ${displaystyle i}$ перед ${displaystyle i}$.

${displaystyle v (i) ~~ = ~~ # {kmid k> i ~ land ~ pi ^ {- 1} (k)$

Счетчик левой инверсии ${displaystyle l}$:
С основанный на месте определение ${displaystyle l (i)}$ - количество инверсий, больше (правый) компонент ${displaystyle i}$.

${displaystyle l (i)}$ это количество элементов в ${displaystyle pi}$ лучше чем ${displaystyle pi (i)}$ перед ${displaystyle pi (i)}$.

${displaystyle l (i) ~~ = ~~ # left {kmid k$ pi (i) ight}}

Правый счет инверсии ${displaystyle r}$, часто называют Код Лемера:
С основанный на месте определение ${displaystyle r (i)}$ - количество инверсий, меньше (слева) компонент ${displaystyle i}$.

${displaystyle r (i)}$ это количество элементов в ${displaystyle pi}$ меньше чем ${displaystyle pi (i)}$ после ${displaystyle pi (i)}$.

${displaystyle r (i) ~~ = ~~ # {kmid k> i ~ land ~ pi (k)$

И то и другое ${displaystyle v}$ и ${displaystyle r}$ можно найти с помощью Диаграмма Роте, который представляет собой матрицу перестановки, в которой единицы представлены точками, и инверсия (часто представленная крестиком) в каждой позиции, где точка справа и ниже. ${displaystyle r (i)}$ это сумма инверсий в строке ${displaystyle i}$ диаграммы Роте, а ${displaystyle v (i)}$ это сумма инверсий в столбце ${displaystyle i}$. Матрица перестановок обратного является транспонированной, поэтому ${displaystyle v}$ перестановки ${displaystyle r}$ его обратного, и наоборот.

Пример: все перестановки четырех элементов

Шесть возможных инверсий 4-элементной перестановки

В следующей сортируемой таблице показаны 24 перестановки четырех элементов с их наборами инверсии на основе места, векторами, связанными с инверсией, и числами инверсии. (Маленькие столбцы являются отражением столбцов рядом с ними, и их можно использовать для сортировки колексикографический порядок.)

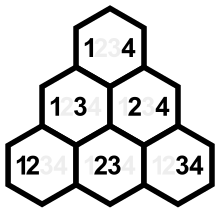
Видно, что ${displaystyle v}$ и ${displaystyle l}$ всегда иметь одинаковые цифры, и это ${displaystyle l}$ и ${displaystyle r}$ оба связаны с набором инверсии по месту. Нетривиальные элементы ${displaystyle l}$ - суммы убывающих диагоналей показанного треугольника, а диагонали ${displaystyle r}$ - суммы возрастающих диагоналей. (Пары в нисходящих диагоналях имеют общие правые компоненты 2, 3, 4, а пары в восходящих диагоналях имеют общие левые компоненты 1, 2, 3.)

Порядок таблицы по умолчанию - обратный порядок колекса по ${displaystyle pi}$, что совпадает с порядком колекса ${displaystyle l}$. Лекс заказывается ${displaystyle pi}$ то же самое, что и lex order by ${displaystyle r}$.

3-элементные перестановки для сравнения
0 1 2 3 4 5 ${displaystyle pi}$ ${displaystyle v}$ ${displaystyle l}$ п-б ${displaystyle r}$ # 0 123 321 000 000 000 000 000 000 0 1 213 312 100 001 010 010 100 001 1 2 132 231 010 010 100 001 010 010 1 3 312 213 110 011 110 011 200 002 2 4 231 132 200 002 200 002 110 011 2 5 321 123 210 012 210 012 210 012 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

${displaystyle pi}$ ${displaystyle v}$ ${displaystyle l}$ п-б ${displaystyle r}$ # 0 1234 4321 0000 0000 0000 0000 0000 0000 0 1 2134 4312 1000 0001 0010 0100 1000 0001 1 2 1324 4231 0100 0010 0100 0010 0100 0010 1 3 3124 4213 1100 0011 0110 0110 2000 0002 2 4 2314 4132 2000 0002 0200 0020 1100 0011 2 5 3214 4123 2100 0012 0210 0120 2100 0012 3 6 1243 3421 0010 0100 1000 0001 0010 0100 1 7 2143 3412 1010 0101 1010 0101 1010 0101 2 8 1423 3241 0110 0110 1100 0011 0200 0020 2 9 4123 3214 1110 0111 1110 0111 3000 0003 3 10 2413 3142 2010 0102 1200 0021 1200 0021 3 11 4213 3124 2110 0112 1210 0121 3100 0013 4 12 1342 2431 0200 0020 2000 0002 0110 0110 2 13 3142 2413 1200 0021 2010 0102 2010 0102 3 14 1432 2341 0210 0120 2100 0012 0210 0120 3 15 4132 2314 1210 0121 2110 0112 3010 0103 4 16 3412 2143 2200 0022 2200 0022 2200 0022 4 17 4312 2134 2210 0122 2210 0122 3200 0023 5 18 2341 1432 3000 0003 3000 0003 1110 0111 3 19 3241 1423 3100 0013 3010 0103 2110 0112 4 20 2431 1342 3010 0103 3100 0013 1210 0121 4 21 4231 1324 3110 0113 3110 0113 3110 0113 5 22 3421 1243 3200 0023 3200 0023 2210 0122 5 23 4321 1234 3210 0123 3210 0123 3210 0123 6

Слабый порядок перестановок

Пермутоэдр симметричная группа S₄

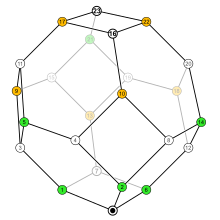
Набор перестановок на п элементам можно придать структуру частичный заказ, называется слабый порядок перестановок, что образует решетка.

Диаграмма Хассе множеств инверсии, упорядоченная подмножество отношения формируют скелет из пермутоэдр.

Если перестановка назначается каждому набору инверсии с использованием определения на основе места, результирующий порядок перестановок соответствует порядку перестановок, где ребро соответствует перестановке двух элементов с последовательными значениями. Это слабый порядок перестановок. Идентичность - это ее минимум, а перестановка, образованная обращением идентичности, - ее максимум.

Если бы перестановка была назначена каждому набору инверсии с использованием определения на основе элементов, результирующий порядок перестановок был бы порядком Граф Кэли, где ребро соответствует перестановке двух элементов в последовательных местах. Этот граф Кэли симметрической группы подобен своему пермутоэдру, но с каждой перестановкой, замененной своей обратной.

Смотрите также

В Викиверситете есть учебные ресурсы о Инверсия (дискретная математика)

Викискладе есть медиафайлы по теме Инверсия (дискретная математика).

• Факторная система счисления
• Граф перестановок
• Транспозиции, простые транспозиции, инверсии и сортировка
• Расстояние Дамерау – Левенштейна
• Четность перестановки

Последовательности в OEIS:

• Последовательности, относящиеся к факторному базовому представлению
• Факторные числа: A007623 и A108731
• Номера инверсий: A034968
• Наборы инверсий конечных перестановок, интерпретируемых как двоичные числа: A211362 (родственная перестановка: A211363)
• Конечные перестановки, в векторах инверсии которых есть только нули и единицы: A059590 (их наборы инверсии: A211364)
• Количество перестановок п элементы с k инверсии; Махонианские числа: A008302 (их максимумы строк; числа Кендалла-Манна: A000140)
• Количество связанных помеченных графов с п края и п узлы: A057500

использованная литература

1. ^ Aigner 2007, стр.27.
2. ^ Контет 1974, с. 237.
3. ^ ^{а б} Кнут 1973, стр.11.
4. ^ Пеммараджу и Скиена 2003, стр.69.
5. ^ ^{а б} Vitter & Flajolet 1990С. 459.
6. ^ ^{а б} Бона 2012, стр.57.
7. ^ Cormen et al. 2001 г., стр.39.
8. ^ ^{а б} Барт и Мутцель 2004, стр.183.
9. ^ ^{а б} Гратцер 2016, стр.221.
10. ^ Махмуд 2000С. 284.
11. ^ Клейнберг и Тардос 2005, стр.225.
12. ^ Вайсштейн, Эрик В. «Вектор инверсии» От MathWorld- Веб-ресурс Wolfram
13. ^ Обратный колексный порядок финитарных перестановок (последовательность A055089 в OEIS)

Библиография источников

• Айгнер, Мартин (2007). «Представление слова». Курс по перечислению. Берлин, Нью-Йорк: Springer. ISBN 3642072534.
• Барт, Вильгельм; Муцель, Петра (2004). «Простой и эффективный двухслойный кросс-счет». Журнал графических алгоритмов и приложений. 8 (2): 179–194. Дои:10.7155 / jgaa.00088.
• Бона, Миклош (2012). «2.2. Инверсии в перестановках мультимножеств». Комбинаторика перестановок. Бока-Ратон, Флорида: CRC Press. ISBN 1439850518.
• Контет, Луи (1974). «6.4 Обращения перестановки [n]». Продвинутая комбинаторика; искусство конечных и бесконечных расширений. Дордрехт, Бостон: D. Reidel Pub. Co. ISBN 9027704414.
• Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001). Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-53196-8.
• Гратцер, Джордж (2016). «7-2 Основные объекты». Теория решеток. специальные темы и приложения. Чам, Швейцария: Birkhäuser. ISBN 331944235X.
• Клейнберг, Джон; Тардос, Ива (2005). Разработка алгоритма. ISBN 0-321-29535-8.
• Кнут, Дональд (1973). «5.1.1 Инверсии». Искусство компьютерного программирования. Аддисон-Уэсли Паб. Co. ISBN 0201896850.
• Махмуд, Хосам Махмуд (2000). «Сортировка неслучайных данных». Сортировка: теория распределения. Серия Wiley-Interscience по дискретной математике и оптимизации. 54. Wiley-IEEE. ISBN 978-0-471-32710-3.
• Pemmaraju, Sriram V .; Скиена, Стивен С. (2003). «Перестановки и комбинации». Вычислительная дискретная математика: комбинаторика и теория графов в системе Mathematica. Издательство Кембриджского университета. ISBN 978-0-521-80686-2.
• Vitter, J.S .; Флажолет, доктор наук (1990). «Средний случай анализа алгоритмов и структур данных». В ван Леувен, Ян (ред.). Алгоритмы и сложность. 1 (2-е изд.). Эльзевир. ISBN 978-0-444-88071-0.

дальнейшее чтение

• Марголиус, Барбара Х. (2001). «Перестановки с инверсиями». Журнал целочисленных последовательностей. 4.

Меры пресортированности

• Маннила, Хейкки (1984). «Меры пресортированности и оптимальные алгоритмы сортировки». Конспект лекций по информатике. 172: 324–336. Дои:10.1007/3-540-13345-3_29.
• Эстивиль-Кастро, Владимир; Вуд, Дерик (1989). «Новая мера пресортированности». Информация и вычисления. 83 (1): 111–119. Дои:10.1016/0890-5401(89)90050-3.
• Скиена, Стивен С. (1988). «Посягающие списки как мера предварительной сортировки». НЕМНОГО. 28 (4): 755–784. Дои:10.1007 / bf01954897.