WikiDer > Дырявое ведро
В дырявое ведро алгоритм, основанный на аналогия о том, как ведро с постоянным утечка переполнится, если средний скорость, с которой наливается вода, превышает скорость, с которой ведро протекает, или если за один раз наливается больше воды, чем вместимость ведра. Его можно использовать для определения того, является ли некоторая последовательность дискретных событий соответствует к определенным пределам их средней и пиковой скорости или частоты, например ограничить действия, связанные с этими событиями, этими ставками или отложить их до тех пор, пока они не будут соответствовать этим ставкам. Его также можно использовать для проверки соответствия или ограничения только средней скорости, то есть для удаления любых отклонений от средней.
Он используется в с коммутацией пакетов компьютерная сеть и телекоммуникации сети как в контроль дорожного движения и формирование трафика из передача данных, в виде пакеты,[примечание 1] к определенным пределам пропускная способность и вспыльчивость (мера неравномерности или вариаций движение течь). Его также можно использовать как алгоритм планирования для определения времени передачи, которое будет соответствовать ограничениям, установленным для полосы пропускания и пакетной передачи, применяемым сетью: см. сетевой планировщик.[1][2][3][4] Вариант дырявого ведра, общий алгоритм скорости передачи ячеек, рекомендуется для асинхронный режим передачи (Банкоматы) сети[5] в Использование / Управление параметрами сети в пользовательско-сетевые интерфейсы или межсетевые интерфейсы или межсетевые интерфейсы к защищать сеть от чрезмерных уровней трафика на маршрутизируемых через нее соединениях. Общий алгоритм скорости передачи ячеек или его эквивалент также может использоваться для форма передачи сетевая карта в сеть банкоматов (то есть на стороне пользователя пользовательско-сетевого интерфейса), например до уровней ниже уровней, установленных для управления использованием / параметрами сети в сети, чтобы предотвратить дальнейшее ограничение этого соединения. Алгоритм дырявого ведра также используется в счетчиках дырявого ведра, например чтобы определить, когда средняя или пиковая скорость случайный или стохастический события или случайные процессы, например, сбои или отказы, выходят за установленные пределы.
По крайней мере, некоторые реализации дырявого ведра являются зеркальным отражением Ведро токенов алгоритм и будет при заданных эквивалентных параметрах определять точно такую же последовательность событий, чтобы соответствовать или не соответствовать одним и тем же ограничениям. Однако есть как минимум два разных описания дырявого ведра, которые могут вызвать путаницу.[1][2][6]
Обзор
В литературе описаны два различных метода применения этой аналогии с дырявым ведром.[1][2][3][4] Они дают то, что кажется двумя разными алгоритмами, оба из которых называются алгоритмом дырявого ведра и, как правило, без ссылки на другой метод. Это привело к путанице в отношении того, что такое алгоритм дырявого ведра и каковы его свойства.
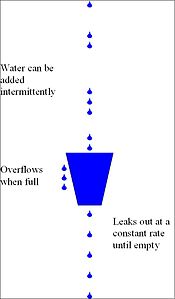
В одном из вариантов применения аналогии аналог ведра - это счетчик или переменная, отдельная от потока трафика или планирования событий.[1][3][4] Этот счетчик используется только для проверки того, что трафик или события соответствуют ограничениям: счетчик увеличивается, когда каждый пакет прибывает в точку, где выполняется проверка или происходит событие, что эквивалентно способу, которым вода периодически добавляется в ведро. Счетчик также уменьшается с фиксированной скоростью, эквивалентной тому, как вода вытекает из ведра. В результате значение счетчика представляет собой уровень воды в аналогичном ведре. Если значение счетчика остается ниже заданного предельного значения при поступлении пакета или возникновении события, т. Е. Сегмент не переполняется, это указывает на его соответствие ограничениям полосы пропускания и пакетной передачи или ограничениям для событий средней и пиковой скорости. Таким образом, в этой версии аналог воды переносится пакетами или событиями, добавляется в ведро при их прибытии или возникновении, а затем утекает. Эта версия упоминается здесь как дырявое ведро как метр.
Во втором варианте аналог ведра - очередь в потоке трафика.[2] Эта очередь используется для непосредственного управления этим потоком: пакеты помещаются в очередь по мере их поступления, что эквивалентно добавлению воды в ведро. Затем эти пакеты удаляются из очереди (первым прибыл - первым обслужен Эквивалент в русском языке: поздний гость гложет и кость), обычно по фиксированной ставке, например для дальнейшей передачи эквивалентно утечке воды из ведра. В результате скорость, с которой обслуживается очередь, напрямую контролирует скорость дальнейшей передачи трафика. Таким образом, он налагает соответствие, а не его проверку, и если очередь обслуживается с фиксированной скоростью (и где все пакеты имеют одинаковую длину), результирующий поток трафика обязательно лишен пакетности или дрожания. Таким образом, в этой версии сам трафик является аналогом воды, проходящей через ведро. Непонятно, как эту версию применения аналогии можно использовать для проверки частоты дискретных событий. Эта версия упоминается здесь как дырявое ведро как очередь.
Дырявое ведро как метр в точности эквивалентно (зеркальному отображению) ведро токенов алгоритм, то есть процесс добавления воды в дырявое ведро точно отражает процесс удаления токенов из токен-ведра, когда приходит соответствующий пакет, процесс утечки воды из дырявого ведра точно отражает процесс регулярного добавления токенов в токен-ведро, и проверка того, что дырявое ведро не переполнится, является зеркалом проверки того, что ведро токенов содержит достаточно токенов и не будет «переполнено». Таким образом, при заданных эквивалентных параметрах два алгоритма будут рассматривать один и тот же трафик как соответствующий или несоответствующий. Дырявое ведро как очередь можно рассматривать как частный случай дырявого ведра как счетчика.[6]
Как метр
Джонатан С. Тернер зачисляется[7] с исходным описанием алгоритма дырявого ведра и описывает его следующим образом: «Счетчик, связанный с каждым пользователем, выполняющим передачу по соединению, увеличивается каждый раз, когда пользователь отправляет пакет, и периодически уменьшается. Если счетчик превышает пороговое значение при увеличении, сеть отбрасывает пакет. Пользователь указывает скорость, с которой счетчик уменьшается (это определяет среднюю полосу пропускания) и значение порога (мера пакетности) ".[1] Бакет (аналог счетчика) в этом случае используется как счетчик для проверки соответствия пакетов, а не как очередь для непосредственного управления ими.
Еще одно описание того, что по сути является той же версией алгоритма счетчика, общий алгоритм скорости передачи ячеек, дается ITU-T в рекомендации I.371 и в Форум банкоматовСпецификация UNI.[3][4] Описание, в котором термин ячейка эквивалентно пакет в описании Тернера[1] дается ITU-T следующим образом: «Дырявое ведро с непрерывным состоянием можно рассматривать как ведро с конечной емкостью, реальное содержание которого истощается с постоянной скоростью 1 единица содержания в единицу времени и содержание которого увеличивается на приращение Т для каждой соответствующей ячейки ... Если при поступлении ячейки содержимое корзины меньше или равно предельному значению τ, значит клетка конформная; в противном случае ячейка не соответствует требованиям. Вместимость ковша (верхняя граница счетчика) составляет (Т + τ)".[4] В этих спецификациях также указано, что из-за его конечной емкости, если содержимое корзины на момент проверки соответствия превышает предельное значение, и, следовательно, ячейка не соответствует требованиям, то корзина остается неизменной; то есть воду просто не добавляют, если это приведет к переполнению ведра.
Дэвид Э. МакДайсан и Даррел Л. Спон комментируют описание, данное Форумом ITU-T / ATM. В этом они заявляют: «В аналогии с дырявым ведром ячейки [банкомата] на самом деле не протекают через ведро; это происходит только при проверке на соответствие допуску».[6] Однако, что нечасто в описаниях в литературе, МакДайсан и Спон также называют алгоритм дырявого ведра очередью, продолжая: «Обратите внимание, что одна из реализаций формирования трафика состоит в том, чтобы фактически обеспечить прохождение ячеек через ведро».[6]
При описании работы версии алгоритма ITU-T МакДайсан и Спон ссылаются на «понятие, обычно используемое в теория массового обслуживания вымышленного «гремлина».[6] Этот гремлин проверяет уровень в ведре и принимает меры, если уровень выше предельного значения. τ : при контроле за соблюдением правил (рис. 2) он открывает люк, в результате чего прибывающий пакет падает и вода не попадает в ведро; при формировании (рис. 3) он поднимает клапан, который задерживает прибывающий пакет и не дает ему доставить воду, пока уровень воды в ведре не упадет ниже τ.
Разница между описаниями Тернера и ITU-T / ATM Forum заключается в том, что Тернер специфичен для контроль дорожного движения, в то время как форум ITU-T / ATM применим как к контролю трафика, так и к формированию трафика. Кроме того, Тернер не утверждает, что на содержимое счетчика должны влиять только соответствующие пакеты, и должно увеличиваться только тогда, когда это не приведет к превышению лимита, т.е. Тернер не указывает явно, что емкость корзины или максимальное значение счетчика конечно. Чтобы описание Тернера было четко согласовано с ITU-T, утверждение «Если счетчик превышает пороговое значение при увеличении, сеть отбрасывает пакет» необходимо изменить на что-то вроде «Если счетчик превысит порог [эквивалентный глубина ковша, T + τ, в описании ITU-T] после увеличения сеть отбрасывает пакет, и счетчик не увеличивается », т.е. он увеличивается только тогда, когда он меньше или равен предельному значению, τили, по крайней мере, на T меньше, чем глубина сегмента в описании ITU-T.
Хотя описание, данное Тернером, не утверждает, что на счетчик должны влиять только соответствующие пакеты, оно дается в терминах функции контроля трафика, где чрезмерное усердие в ограничении соединения, содержащего несоответствующие пакеты, может не быть проблемой. Действительно, в некоторых контекстах, например переменный битрейт (VBR), потеря любого одного пакета может привести к повреждению всего сообщения более высокого уровня, например PDU сетевого уровня OSI. В этом случае отбрасывание всех следующих пакетов этого поврежденного PDU снижает ненужную нагрузку на сеть. Однако было бы совершенно неприемлемо при формировании трафика для пакета, который не прошел тест на соответствие, влиять на то, как долго до следующего соответствия может произойти, то есть если акт тестирования последующего пакета на соответствие изменит, как долго пакет, ожидающий соответствия в данный момент, будет ждать. Это именно то, что произошло бы, если бы воду из несоответствующих пакетов добавить в ведро, поскольку любые последующие несоответствующие пакеты поднимут уровень воды и, таким образом, заставят пакет, ожидающий согласования, ждать дольше.
Ни Тернер, ни ITU-T не решают проблему пакетов переменной длины. Однако описание согласно ITU-T предназначено для ячеек ATM, которые представляют собой пакеты фиксированной длины, и Тернер специально не исключает пакеты переменной длины. Следовательно, в обоих случаях, если величина, на которую увеличивается содержимое корзины или счетчик для соответствующего пакета, пропорциональна длине пакета, они оба будут учитывать длину и позволяют алгоритму явно ограничивать полосу пропускания трафика, а не ограничение скорости передачи пакетов. Например, более короткие пакеты добавят меньше в корзину и, следовательно, могут прибыть с меньшими интервалами; тогда как более длинные пакеты добавят больше и, следовательно, должны быть разделены пропорционально большими интервалами для соответствия.
Концепция работы
Описание концепции работы алгоритма Leaky Bucket как счетчика, который может использоваться либо для контроля трафика, либо для формирования трафика, можно сформулировать следующим образом:
- Корзина фиксированной емкости, связанная с каждым виртуальным подключением или пользователем, протекает с фиксированной скоростью.
- Если ведро пустое, оно перестанет протекать.
- Чтобы пакет соответствовал требованиям, должна быть возможность добавить определенное количество воды в ведро: конкретное количество, добавляемое соответствующим пакетом, может быть одинаковым для всех пакетов или может быть пропорционально длине пакета.
- Если такое количество воды приведет к превышению емкости ведра, значит, пакет не соответствует требованиям, и вода в ведре останется неизменной.
Использует
Дырявое ведро в качестве счетчика можно использовать как в формирование трафика или контроль дорожного движения. Например, в сетях ATM в форме общего алгоритма скорости передачи ячеек он используется для сравнения полосы пропускания и пакетной передачи трафика на виртуальном канале (VC) или виртуальном пути (VP) с заданными пределами скорости, с которой могут прибыть ячейки и максимальное дрожание или изменение интервалов между поступлениями для VC или VP. При контроле трафика ячейки, которые не соответствуют этим ограничениям (несоответствующие ячейки), могут быть отброшены (отброшены) или могут иметь пониженный приоритет (для функций управления трафиком в нисходящем направлении отключаются в случае перегрузки). При формировании трафика ячейки задерживаются до тех пор, пока не будут соответствовать. Контроль трафика и формирование трафика обычно используются в UPC / NPC для защиты сети от избыточного или чрезмерно скачкообразного трафика, см. управление пропускной способностью и предотвращение перегрузки. Формирование трафика обычно используется в сетевых интерфейсах в хозяева для предотвращения передачи, превышающей пределы полосы пропускания или джиттера, и отбрасываемой функциями управления трафиком в сети. (Видеть планирование (вычисление) и сетевой планировщик.)
Алгоритм дырявого ведра в качестве измерителя может также использоваться в счетчике дырявого ведра для измерения скорости случайного или случайные процессы. Счетчик Leaky bucket может использоваться для определения того, когда средняя или пиковая частота событий превышает некоторый приемлемый фоновый уровень, то есть когда ведро переполняется.[8] Однако события, которые не вызывают переполнения, т.е. имеют достаточно низкие скорости и хорошо распределяются во времени, можно игнорировать. Например, такой счетчик дырявого ведра можно использовать для обнаружения внезапного всплеска исправимых ошибок памяти или постепенного, но значительного увеличения средней скорости, что может указывать на надвигающийся отказ.[9] и т.п.
Использование алгоритма дырявого ведра в счетчике дырявого ведра аналогично таковому в управлении трафиком в том смысле, что он используется в качестве счетчика. По сути, события заменяют пакеты в описании, при этом каждое событие вызывает добавление воды в ведро. Если в результате события корзина переполнится, событие должно инициировать действие, связанное с событием выхода за пределы. Некоторые реализации[8] кажется параллельным описанию Тернера,[1] в том, что нет явного ограничения на максимальное значение, которое может принимать счетчик, подразумевая, что после того, как счетчик превысил порог, он не может вернуться в свое предыдущее состояние до тех пор, пока не пройдет период, значительно превышающий эквивалент интервала выброса, которые могут быть увеличены тем, что в противном случае было бы соответствующими событиями. Однако другие реализации могут не увеличивать счетчик, когда он переполнен, что позволяет ему правильно определять, соответствуют ли следующие события или нет.
Параметры
В случае алгоритма дырявого ведра в качестве счетчика ограничениями трафика могут быть полоса пропускания и периодичность выходных данных.[3][4][заметка 2]
Предел полосы пропускания и предел пакетной передачи для соединения могут быть указаны в договор перевозки. Предел пропускной способности может быть указан как пакет или частота кадров, байт или битрейт, или как интервал выбросов между пакетами. Предел прерывистости может быть указан как дрожь или изменение задержки терпимость, или как максимальный размер пакета (МБС).
Множественные наборы параметров контракта могут применяться одновременно к соединению с использованием нескольких экземпляров алгоритма дырявого ведра, каждый из которых может принимать полосу пропускания и предел пакетной передачи: см. Контроллер двойного протекающего ведра.
Интервал выброса
Скорость, с которой происходит утечка из ведра, будет определять предел пропускной способности, который Тернер называет средней скоростью.[1] и обратное значение которого МСЭ-Т называет интервалом передачи. Проще всего объяснить, что это за интервал, когда пакеты имеют фиксированную длину. Следовательно, первая часть этого описания предполагает это, и последствия переменной длины пакета рассматриваются отдельно.
Рассмотрим бакет, который точно заполнен до верха предшествующим трафиком, т. Е. Когда уже произошла максимально разрешенная пиковая скорость, т. Е. Максимальное количество пакетов или ячеек только что прибыло за минимальное количество времени, чтобы они по-прежнему соответствовали полосе пропускания и пределы джиттера. Минимальный интервал до того, как следующий пакет может соответствовать требованиям, - это время, необходимое ведру для утечки точно такого же количества воды, которое доставлено пакетом, и если пакет протестирован и соответствует требованиям в это время, это точно заполнит ведро еще раз. . Таким образом, как только бакет заполнен, максимальная скорость, которой могут соответствовать пакеты, соответствует этому интервалу между каждым пакетом.
Тернер[1] относится к этой скорости как к средней, подразумевая, что ее обратной величиной является средний интервал. Однако есть некоторая двусмысленность в том, что такое средняя частота и интервал. Поскольку пакеты могут поступать с любой более низкой скоростью, это верхняя граница, а не фиксированное значение, поэтому его в лучшем случае можно назвать максимумом для средней скорости. Кроме того, во время максимальной пакетной передачи пакеты могут приходить с меньшими интервалами и, следовательно, с более высокой скоростью, чем эта. Таким образом, для любого периода меньше бесконечности фактическая средняя скорость может быть (но не обязательно) больше, чем это, а средний интервал может быть (но не обязательно) меньше, чем интервал выбросов. Следовательно, из-за этой неоднозначности в дальнейшем используется термин интервал выбросов. Однако верно то, что минимальное значение, которое может принимать долгосрочный средний интервал, обычно является интервалом выбросов.
Для пакетов переменной длины, где количество, добавляемое в ведро, пропорционально длине пакета, максимальная скорость, с которой они могут соответствовать, зависит от их длины: количество, которое должно вытекать из полного ведра, чтобы пакет соответствовал требованиям, является Сумма, которую добавит пакет, и, если она пропорциональна длине пакета, таков интервал между ним и предыдущим пакетом, заполнившим корзину. Следовательно, невозможно указать конкретный интервал передачи для пакетов переменной длины, и предел полосы пропускания должен быть указан явно в битах или байтах в секунду.
Допуск изменения задержки
Проще всего объяснить, что это за допуск, если пакеты имеют фиксированную длину. Следовательно, первая часть этого описания предполагает это, и последствия переменной длины пакета рассматриваются отдельно.
ITU-T определяет предельное значение, τ, что меньше вместимости ковша на Т (величина, на которую увеличивается содержимое корзины для каждой соответствующей ячейки), так что емкость ведра равна Т + τ. Это предельное значение указывает, насколько раньше пакет может прибыть, чем обычно можно было бы ожидать, если бы пакеты приходили с точно интервалом передачи между ними.
Представьте себе следующую ситуацию: ведро протекает со скоростью 1 единицу воды в секунду, поэтому предельное значение τ и количество воды, добавленной пакетом, Т, фактически выражаются в секундах. Это ведро сначала пустое, поэтому, когда пакет попадает в ведро, он не полностью заполняет ведро, добавляя в него воду. Т, и ведро теперь τ ниже его мощности. Таким образом, когда прибывает следующий пакет, ведро должно быть только опорожнено Т – τ чтобы это соответствовало. Таким образом, интервал между этими двумя пакетами может достигать τ меньше, чем Т.
Это распространяется на несколько пакетов в последовательности: Представьте себе следующее: корзина снова начинается пустой, поэтому первый приходящий пакет должен соответствовать. Затем корзина становится полностью заполненной после нескольких соответствующих пакетов, N, прибыли в минимально возможное время для соответствия. Для последнего ( Nй) пакет соответствует требованиям, ведро должно было протечь достаточное количество воды из предыдущего N - 1 пакетик ((N – 1) * Т секунд), чтобы оно было точно на предельном значении τ в это время. Следовательно, утечка воды составляет (N – 1)Т – τ, что, поскольку утечка составляет одну единицу в секунду, потребовалось ровно (N – 1)Т – τ секунд до утечки. Таким образом, самое короткое время, за которое все N пакеты могут приходить и соответствовать (N – 1)Т – τ секунд, что ровно τ меньше, чем время, которое потребовалось бы, если бы пакеты приходили точно в интервал передачи.
Однако пакеты могут приходить только с интервалами меньше, чем Т где корзина не заполнена предыдущим пакетом. Если это так, значит, ведро должно быть опорожнено на полную Т до того, как следующий пакет соответствует. Таким образом, как только этот допуск будет использован пакетами, приходящими менее чем на Т, последующие кадры должны поступать с интервалами не менее Т. Однако они могут прибыть через более длительные промежутки времени, когда ведро не будет заполнено ими. Когда это произошло, пакеты снова могут приходить с интервалами меньше, чем Т до тех пор, пока допуск не будет снова использован. Однако, поскольку ведро перестает протекать, когда оно пустое, всегда есть предел (τ), насколько допускаются интервалы, превышающие Тоднако гораздо больше, чем Т они могут быть или, однако, многие из них есть.
Поскольку предельное значение τ определяет, насколько раньше пакет может прибыть, чем можно было бы ожидать, это предел разницы между максимальной и минимальной задержками от источника до точки, где выполняется проверка соответствия (при условии, что пакеты генерируются без джиттера). Следовательно, для этого параметра в ATM используется термин "допуск изменения задержки ячейки" (CDVt).
В качестве примера возможный источник изменения задержки - это когда несколько соединений (потоки пакетов) мультиплексируются вместе на выходе коммутатора. Предполагая, что сумма полос пропускания этих соединений меньше, чем у выходных, все поступающие пакеты могут быть в конечном итоге переданы. Однако, если их прибытия независимы, например поскольку они поступают на разные входы коммутатора, то несколько сигналов могут поступать или почти одновременно. Поскольку выход может передавать только один пакет за раз, остальные должны быть помещены в очередь в буфере, пока не наступит их очередь для передачи. Затем этот буфер вводит дополнительную задержку между пакетом, поступающим на вход и передаваемым выходом, и эта задержка варьируется в зависимости от того, сколько других пакетов уже поставлено в очередь в буфере. Аналогичная ситуация может возникнуть на выходе хоста (в сетевой карте), когда несколько пакетов имеют одинаковое или похожее время выпуска, и эту задержку обычно можно смоделировать как задержку в виртуальном буфере вывода.
Для пакетов переменной длины, когда количество воды, добавляемой данным пакетом, пропорционально его длине, τ не может рассматриваться как ограничение на то, насколько полным может быть бакет при поступлении пакета, поскольку это зависит от размера пакета. Однако время, необходимое для слива с этого уровня до пустого, по-прежнему зависит от того, насколько раньше пакет может прибыть, чем ожидалось, когда пакеты передаются с предельной полосой пропускания. Таким образом, допустимое максимальное отклонение задержки передачи до точки, в которой применяется тест на соответствие, и, следовательно, допуск на максимальное изменение задержки.
Максимальный размер пакета
Предельное значение или допуск изменения задержки также контролирует, сколько пакетов может прибыть в пачке, что определяется превышением глубины сегмента над емкостью, требуемой для одного пакета. Следовательно, MBS также является мерой пакетной передачи или джиттера, и можно указать пакетную передачу как MBS и получить предельное значение. τ из этого или указать его как значение допуска / предела вариации джиттера / задержки и получить из этого MBS.
Пакет или группа пакетов может достигать более высокой скорости, чем определено интервалом передачи. Т. Это может быть линейная скорость соединения физического уровня, когда пакеты в пакете будут приходить друг за другом. Однако, как и в ATM, допуск может применяться к более низкой скорости, в этом случае Устойчивая скорость передачи ячеек (SCR), и пачка пакетов (ячеек) может поступать с более высокой скоростью, но меньшей, чем линейная скорость физического уровня, в этом случае Пиковая скорость передачи ячеек (ПЦР). Тогда MBS может быть количеством ячеек, необходимых для транспортировки пакета более высокого уровня (см. сегментация и повторная сборка), где пакеты передаются с максимальной полосой пропускания, определяемой SCR, а ячейки в пакетах передаются в PCR; таким образом позволяя последней ячейке пакета и самому пакету прибыть значительно раньше, чем если бы ячейки были отправлены в SCR: продолжительность передачи = (MBS-1) / PCR, а не (MBS-1) / SCR. Этот всплеск PCR значительно увеличивает нагрузку на общие ресурсы, например переключение выходных буферов, чем передача в SCR, и, таким образом, более вероятно, что это приведет к переполнению буфера и перегрузке сети. Однако он создает меньшую нагрузку на эти ресурсы, чем передача в SCR с предельным значением, τSCR, что позволяет передавать и прибывать ячейки MBS с линейной скоростью.
Если предельное значение достаточно велико, то несколько пакетов могут прибыть пачкой и по-прежнему соответствовать: если корзина начинается с пустой, первый прибывший пакет добавит Т, но если к моменту прибытия следующего пакета его содержимое будет ниже τ, это также будет соответствовать. Предполагая, что каждый пакет занимает δ прибыть, то если τ (выражается как время, необходимое для опорожнения ведра от предельного значения) равно или больше интервала выброса за вычетом минимального времени между прибытием, Т – δ, второй пакет будет соответствовать, даже если он придет в виде пакета с первым. Аналогично, если τ равно или больше (Т – δ) × 2, тогда 3 пакета могут прийти пачкой и т. Д.
Максимальный размер этого пакета, M, можно рассчитать из интервала выбросов, Т; максимальный допуск джиттера, τ; и время, необходимое для передачи / приема пакета, δ, следующим образом:[3]
В равной степени минимальное значение допуска джиттера τ который дает конкретный MBS, может быть рассчитан из MBS следующим образом:[3]
В случае ATM, где технически MBS относится только к допуску SCR, в приведенном выше уравнении время, необходимое для доставки каждого пакета, δ, - интервал эмиссии клеток при ПЦР ТПЦР, а интервал эмиссии Т, - интервал излучения СКВ ТSCR. Если MBS должно быть количеством ячеек, необходимых для транспортировки сегментированного пакета, предельное значение, указанное выше, τ, должно быть, что для SCR τSCR. Однако в UNI или NNI, где ячейки в PCR будут подвергаться изменению задержки, это должно быть предельное значение для SCR плюс значение для PCR. τSCR + τПЦР.
Для пакетов переменной длины максимальный размер пакета будет зависеть от длины пакетов в пакете, и нет единого значения для максимального размера пакета. Однако можно указать общую длину пакета в байтах, исходя из байтовой скорости входного потока, эквивалентной байтовой скорости утечки и глубины сегмента.
Сравнение с алгоритмом token bucket
Алгоритм дырявого ведра иногда противопоставляется ведро токенов алгоритм. Однако вышеуказанное концепция работы для дырявого ведра как счетчик можно напрямую сравнить с алгоритмом маркерного ведра, описание которого приводится в этой статье следующим образом:
- Токен добавляется в корзину каждые 1 /р секунд.
- Ведро вмещает не более б жетоны. Если жетон приходит, когда ведро заполнено, он сбрасывается.
- Когда пакет (сетевой уровень PDU) [sic][примечание 1] прибывает "n" байтов, п токены удаляются из корзины, и пакет отправляется в сеть.
- Если меньше чем п токены доступны, токены не удаляются из корзины, и пакет считается несоответствующим.
Это можно сравнить с концепцией работы, повторенной сверху:
- Корзина фиксированной емкости, связанная с каждым виртуальным подключением или пользователем, протекает с фиксированной скоростью.
- Если ведро пустое, оно перестанет протекать.
- Чтобы пакет соответствовал требованиям, должна быть возможность добавить определенное количество воды в ведро: конкретное количество, добавляемое соответствующим пакетом, может быть одинаковым для всех пакетов или может быть пропорционально длине пакета.
- Если такое количество воды приведет к превышению емкости ведра, значит, пакет не соответствует требованиям, и вода в ведре останется неизменной.
Как можно видеть, эти два описания, по сути, являются зеркальным отображением друг друга: одно регулярно что-то добавляет в корзину и что-то убирает для согласования пакетов до нулевого предела; другой регулярно убирает и добавляет для соответствия пакетов до предела емкости корзины. Итак, является ли реализация, которая добавляет токены для соответствующего пакета и удаляет их с фиксированной скоростью, реализацией дырявого ведра или маркерного ведра? Аналогичным образом, какой алгоритм используется в реализации, которая удаляет воду из соответствующего пакета и добавляет воду с фиксированной скоростью? Фактически, оба они фактически одинаковы, то есть реализации как дырявого ведра, так и ведра токенов, поскольку это один и тот же базовый алгоритм, описанный по-разному. Это объясняет, почему при одинаковых параметрах два алгоритма будут видеть одни и те же пакеты как соответствующие или несоответствующие. Таким образом, различия в свойствах и производительности реализаций алгоритмов дырявых и токен-бакетов полностью связаны с различиями в реализациях, т.е.они не связаны с различиями в базовых алгоритмах.
Следует отметить, что алгоритм дырявого ведра, когда он используется в качестве счетчика, может разрешить соответствующий выходной поток пакетов с джиттером или пакетностью, может использоваться как при контроле трафика, так и при формировании, и может быть реализован для пакетов переменной длины.
Как очередь
Дырявое ведро как очередь - это, по сути, способ описания простого ФИФО буфер или очередь, которые обслуживаются с фиксированной скоростью, чтобы удалить скачкообразность или дрожание. Описание этого дается Эндрю С. Таненбаум, в (более старой версии) его книги Компьютерная сеть as "Дырявое ведро состоит из конечной очереди. Когда приходит пакет, если в очереди есть место, он добавляется в очередь; в противном случае он отбрасывается. При каждом такте часов передается один пакет (если очередь не пуста) ".[2] Таким образом, реализация дырявого ведра в виде очереди всегда является формой функции формирования трафика.
Как можно видеть, эта реализация ограничена тем, что пакеты всегда передаются только с фиксированной скоростью. Чтобы подчеркнуть это, Таненбаум также заявляет, что «Алгоритм дырявого ведра обеспечивает жесткую схему вывода со средней скоростью, независимо от того, насколько импульсным является [входной] трафик».[10] Однако это утверждение строго верно только до тех пор, пока очередь не становится пустой: если средняя скорость поступления меньше, чем частота тактов часов, или если входной сигнал достаточно прерывистый, чтобы потери привели к тому, что скорость остатка была ниже тактовая частота (т.е. промежутки во входном потоке достаточно велики, а очередь достаточно мала, чтобы она могла стать пустой), в выходном потоке будут промежутки.
Еще одно ограничение состоит в том, что дырявое ведро как функция формирования трафика очереди передает пакеты только в тактах; следовательно, если он используется в сети, эквивалент UPC и NPC, он также накладывает фиксированную фазу на дальнейшую передачу пакетов. Принимая во внимание, что при использовании счетчика дырявого ведра для управления дальнейшей передачей пакет передается, как только он соответствует, то есть относительно предыдущего или, если он уже соответствует, времени его прибытия; не по каким-то произвольным местным часам. И наоборот, в контексте задержки передачи это наложение фиксированной фазы, которая может со временем отличаться от фазы входящего потока пакетов, в остальном согласованного, составляет изменение задержки и, следовательно, дрожание. Джиттер, вызванный этим конкретным образом, может наблюдаться только тогда, когда задержка измеряется как время прохождения между двумя отдельными точками измерения, одна с каждой стороны дырявого ведра, как функция формирования очереди. Однако в контексте передачи данных в реальном времени именно эта сквозная задержка определяет задержку полученных данных. Следовательно, дырявое ведро как очередь не подходит для передачи трафика в реальном времени.
Ограничение пакетов переменной длины с использованием алгоритма дырявого ведра в качестве очереди значительно сложнее, чем для пакетов фиксированной длины. Таненбаум дает следующее описание дырявого ведра «подсчета байтов» для пакетов переменной длины: «В каждом такте счетчик инициализируется значением n. Если первый пакет в очереди имеет меньше байтов, чем текущее значение счетчика, он передается, и счетчик уменьшается на это количество байтов. Дополнительные пакеты также могут быть отправлены, если счетчик достаточно высок. Когда счетчик падает ниже длины следующего пакета в очереди, передача останавливается до тех пор, пока следующий тик, при котором остаточный счетчик байтов сбрасывается [до n], и поток может продолжаться ».[2] Как и версия для пакетов фиксированной длины, эта реализация сильно влияет на фазу передачи, что приводит к переменным сквозным задержкам и непригодности для формирования трафика в реальном времени.
Использует
Дырявое ведро как очередь можно использовать только в формирование трафик с указанной полосой пропускания без дрожания на выходе.[10] Его можно использовать в сети, например как часть управления полосой пропускания, но больше подходит для формирования трафика в сетевых интерфейсах узлов.
Параметры
В случае алгоритма дырявого ведра в качестве очереди единственным определенным пределом для этого алгоритма является пропускная способность его вывода.[10][заметка 2]
Предел пропускной способности для подключения может быть указан в договор перевозки. Предел пропускной способности может быть указан как пакет или частота кадров, байт или битрейт, или как интервал выбросов между пакетами.
Неэффективность
Реализация дырявого ведра в качестве очереди не позволяет эффективно использовать доступные сетевые ресурсы. Поскольку он передает пакеты только с фиксированными интервалами, будет много случаев, когда объем трафика очень мал и большие части сетевых ресурсов (в частности, пропускная способность) не используются. Поэтому в реализации дырявого ведра в виде очереди не существует механизма, который позволял бы отдельным потокам разгоняться до скорости порта, эффективно потребляя сетевые ресурсы в то время, когда не было бы конкуренции за ресурсы в сети. Однако реализация token bucket и дырявого ведра в качестве счетчика позволяет выходным потокам трафика иметь импульсные характеристики.
Сравнение двух версий
Анализ двух версий алгоритма дырявого ведра показывает, что версия как очередь является частным случаем версии как счетчика.
Представьте себе функцию формирования трафика для пакетов фиксированной длины, которая реализуется с использованием очереди фиксированной длины, формируя элемент задержки, который обслуживается с использованием дырявого ведра в качестве счетчика. Представьте также, что ведро в этом счетчике имеет глубину, равную сумме, добавляемой пакетом, то есть имеет предельное значение, τ, из нуля. Однако проверка на соответствие выполняется только с интервалами интервала передачи, когда передается пакет в начале очереди и в него добавляется вода. Эта вода затем просачивается во время следующего интервала выбросов (или удаляется непосредственно перед выполнением следующего теста на соответствие), позволяя следующему пакету соответствовать тогда или в некотором последующем интервале выбросов. Функцию обслуживания можно также рассматривать с точки зрения корзины с токенами той же глубины, где добавляется достаточно токенов для одного пакета (если корзина не заполнена) с интервалами эмиссии. Эта реализация затем будет принимать пакеты с импульсным шаблоном прибытия (ограниченным глубиной очереди) и передавать их с интервалами, которые всегда являются точными (целыми) кратными интервалу передачи.
Однако реализация дырявого ведра как счетчика (или маркерного ведра) в функции формирования трафика, описанной выше, является точным эквивалентом описания дырявого ведра как очереди:[2] элемент задержки версии счетчика является ведром версии очереди; ведро версии счетчика - это процесс, обслуживающий очередь, а утечка такова, что интервал выбросов совпадает с интервалом тактов. Следовательно, для пакетов фиксированной длины реализация дырявого ведра в виде очереди является частным случаем функции формирования трафика с использованием дырявого ведра (или маркерного ведра) в качестве счетчика, в котором предельное значение τ, равно нулю, и процесс проверки соответствия выполняется с минимально возможной скоростью.
Дырявое ведро как очередь для пакетов переменной длины также может быть описано как эквивалентное частному случаю дырявого ведра как счетчика. Предлагаемая реализация[2] может, как и реализация фиксированной длины, рассматриваться как функция формирования трафика, в которой очередь является элементом задержки, а не ведром, а функция, обслуживающая очередь, в этом случае явно указана как ведро токенов: это уменьшается для соответствующих пакетов и увеличивается с фиксированной скоростью. Следовательно, поскольку дырявое ведро как счетчик и ведро токена эквивалентны, дырявое ведро как очередь для пакетов переменной длины также является частным случаем функции формирования трафика, использующей дырявое ведро (или ведро токена) в качестве счетчика.
Интересное последствие видения дырявого ведра как очереди для пакетов переменной длины как конкретной реализации маркерного ведра или дырявого ведра как счетчика при формировании трафика. Это то, что сегмент счетчика имеет глубину n, и, как всегда бывает с сегментом токенов, эта глубина определяет пакетность выходного трафика (возможно, в отношении среднего или минимального количества токенов, необходимых для пакеты). Следовательно, можно количественно измерить пакетность выходных данных этого дырявого ведра "подсчета байтов" в виде метра, если только все пакеты не имеют максимальной длины, когда это становится бессмысленным. Однако эта способность определять прерывистость вывода находится в прямом противоречии с утверждением, что дырявое ведро (как очередь) обязательно дает вывод с жесткой скоростью, независимо от того, насколько скачкообразно ввод.
Смотрите также
Примечания
- ^ а б В управлении движением дырявое ведро обычно применяется к эквиваленту ISO-Модель OSI слой 2 Уровень канала передачи данных PDU, например Банкомат клетки и Кадры Ethernet, которые называются кадры. Тогда можно утверждать, что описание этого алгоритма должно быть дано в терминах кадры нет пакеты, которые в 7-уровневой модели ISO-OSI являются уровнем 3 Сетевой уровень PDU. Тем не менее, термин «пакет» обычно используется в описании этого алгоритма в литературе, и это соглашение также применяется здесь. Однако это не означает, что алгоритм дырявого ведра применяется исключительно к PDU сетевого уровня.
- ^ а б Функции формирования трафика включают очередь, которая обязательно имеет конечный размер. Следовательно, если входной поток превышает некоторый уровень пакетности, зависящий от длины очереди, или постоянно превышает ограничение полосы пропускания, налагаемое на выходной поток, очередь будет переполняться, и пакеты (обычно) будут отброшены: см. Формирование трафика # Состояние переполнения. Поэтому функции формирования трафика можно рассматривать как применение политик трафика к входному соединению и формирование трафика к выходу. Следовательно, они должны принять параметр для предела всплесков на входе в дополнение к этому или параметрам для дырявого ведра. Однако для этого предела пакетной передачи входных данных по умолчанию может быть установлено значение, которое, как ожидается, не повлияет на нормальный трафик (предполагается, что очередь достаточно глубока для всех нормальных обстоятельств), и не всегда указывается явно.
Рекомендации
- ^ а б c d е ж грамм час я Тернер, Дж., Новые направления в коммуникациях (или какой путь в век информации?). IEEE Communications Magazine 24 (10): 8–15. ISSN 0163-6804, 1986.
- ^ а б c d е ж грамм час Эндрю С. Таненбаум, Компьютерные сети, четвертое издание, ISBN 0-13-166836-6, Prentice Hall PTR, 2003 г., стр. 401.
- ^ а б c d е ж грамм ATM Forum, Пользовательский сетевой интерфейс (UNI), версия 3.1, ISBN 0-13-393828-X, Prentice Hall PTR, 1995.
- ^ а б c d е ж МСЭ-Т, Контроль трафика и контроль перегрузки в B ISDN, Рекомендация I.371, Международный союз электросвязи, 2004 г., Приложение A, стр. 87.
- ^ МСЭ-Т, Контроль трафика и контроль перегрузки в B ISDN, Рекомендация I.371, Международный союз электросвязи, 2004 г., стр. 17
- ^ а б c d е МакДайсан, Дэвид Э. и Спон, Даррел Л., Банкомат: теория и применение, ISBN 0-07-060362-6, Серия McGraw-Hill по компьютерным коммуникациям, 1995, страницы 358–9.
- ^ Эндрю С. Таненбаум, Компьютерные сети, четвертое издание, ISBN 0-13-166836-6, Prentice Hall PTR, 2003, стр. 400.
- ^ а б http://encyclopedia2.thefreedictionary.com/leaky+bucket+counter.
- ^ Intel, Серверная плата Intel S5400SF: Технические характеристики продукта, Сентябрь 2007 г., http://download.intel.com/support/motherboards/server/s5400sf/sb/s5400sf_tps_rev2_01.pdf.
- ^ а б c Эндрю С. Таненбаум, Компьютерные сети, четвертое издание, ISBN 0-13-166836-6, Prentice Hall PTR, 2003, стр. 402.