WikiDer > Logit

Logit

Участок логита (п) в диапазоне от 0 до 1, где основание логарифма равно е.

В статистике логит (/ˈлoʊdʒɪт/ LOH-джит) или функция логарифм это логарифм из шансы ${ displaystyle { frac {p} {1-p}}}$ где $п$ это вероятность.^[1] Это тип функции, которая создает карту значений вероятности из ${ displaystyle (0,1)}$ к ${ Displaystyle (- infty, + infty)}$ ^[2]. Это обратный из сигмовидный «логистическая» функция или логистическая трансформация используется в математика, особенно в статистика.

Определение

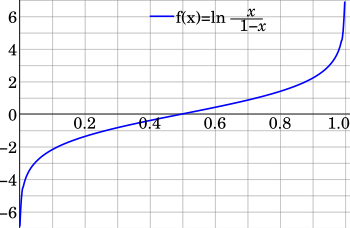
Если $п$ это вероятность, тогда $п /(1 - п)$ соответствующий шансы; то $логит$ вероятности - это логарифм шансов, т.е.

{ Displaystyle OperatorName {logit} (p) = log left ({ frac {p} {1-p}} right) = log (p) - log (1-p) = - log left ({ frac {1} {p}} - 1 right) ,.}

Основа логарифм используемая функция не имеет большого значения в данной статье, если она больше 1, но натуральный логарифм с базой $е$ является наиболее часто используемым. Выбор базы соответствует выбору логарифмическая единица для значения: основание 2 соответствует Шеннон, основание $е$ к «нац”, И основание 10 в Хартли; эти единицы особенно используются в теоретико-информационных интерпретациях. Для каждого выбора базы функция логита принимает значения от отрицательной до положительной бесконечности.

В «Логистическая» функция любого числа ${ displaystyle alpha}$ дается обратным $логит$ :

{ displaystyle operatorname {logit} ^ {- 1} ( alpha) = operatorname {logistic} ( alpha) = { frac {1} {1+ operatorname {exp} (- alpha)}} = { frac { operatorname {exp} ( alpha)} { operatorname {exp} ( alpha) +1}}}

Разница между $логит$ s двух вероятностей - это логарифм отношение шансов ( $р$ ), таким образом, обеспечивая сокращение для записи правильной комбинации отношений шансов только добавлением и вычитанием:

{ displaystyle operatorname {log} (R) = log left ({ frac {{p_ {1}} / (1-p_ {1})} {{p_ {2}} / (1-p_ { 2})}} right) = log left ({ frac {p_ {1}} {1-p_ {1}}} right) - log left ({ frac {p_ {2}} {1-p_ {2}}} right) = operatorname {logit} (p_ {1}) - operatorname {logit} (p_ {2}) ,.}

История

Было предпринято несколько попыток адаптировать методы линейной регрессии к области, где выходом является значение вероятности, ${ displaystyle (0,1)}$ , вместо любого действительного числа ${ Displaystyle (- infty, + infty)}$ . Во многих случаях такие усилия были сосредоточены на моделировании этой проблемы путем отображения диапазона ${ displaystyle (0,1)}$ к ${ Displaystyle (- infty, + infty)}$ а затем запустить линейную регрессию для этих преобразованных значений. В 1934 г. Честер Иттнер Блисс использовал кумулятивную функцию нормального распределения для выполнения этого сопоставления и назвал свою модель пробит сокращение для "проблемаспособность unЭто";^[3]. Однако это более затратно в вычислительном отношении. В 1944 г. Джозеф Берксон использовал журнал шансов и вызвал эту функцию логит сокращение для "бревноИстик ООНЭто"по аналогии с пробитом. Логарифмические коэффициенты широко использовались Чарльз Сандерс Пирс (конец 19 века).^[4]. Г. А. Барнард в 1949 г. ввел широко используемый термин логарифм;^[5] логарифм шансов события - это логит вероятности события.^[6]

Использование и свойства

В логит в логистическая регрессия является частным случаем функции ссылки в обобщенная линейная модель: это канонический функция ссылки для Распределение Бернулли.
В логит функция является отрицательной производная из бинарная функция энтропии.
В логит также является центральным элементом вероятностного Модель раша за измерение, который, среди прочего, применяется в психологической и педагогической оценке.
В обратный логит функция (т.е. логистическая функция) также иногда называют истекать функция.^[7]
В эпидемиология болезней растений Логит используется для соответствия данных логистической модели. В моделях Гомперца и мономолекулярных все три известны как модели семейства Ричардсов.
Логарифмическая функция вероятностей часто используется в оценка состояния алгоритмы^[8] из-за его численных преимуществ в случае малых вероятностей. Вместо умножения очень маленьких чисел с плавающей запятой, вероятности логарифмических шансов можно просто суммировать для вычисления совместной вероятности (логарифмических шансов).^[9]^[10]

Сравнение с пробит

Сравнение функция logit с масштабированным пробитом (т.е. обратным CDF из нормальное распределение), сравнивая

{ displaystyle operatorname {logit} (x)}

vs.

{ displaystyle { tfrac { Phi ^ {- 1} (x)} {, { sqrt { pi / 8 ,}} ,}}}

, что делает уклоны одинаковыми на

у

-источник.

Тесно связан с $логит$ функция (и логит модель) являются пробит функция и пробит модель. В $логит$ и $пробит$ оба сигмовидные функции с доменом от 0 до 1, что делает их обоих квантильные функции - т.е. инверсии кумулятивная функция распределения (CDF) распределение вероятностей. Фактически, $логит$ это квантильная функция из логистическая дистрибуция, в то время $пробит$ квантильная функция нормальное распределение. В $пробит$ функция обозначается ${ Displaystyle Phi ^ {- 1} (х)}$ , где ${ Displaystyle Phi (х)}$ это CDF нормального распределения, как уже упоминалось:

{ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ {- { frac {y ^ {2} } {2}}} dy.}

Как показано на графике справа, $логит$ и $пробит$ функции очень похожи, когда $пробит$ функция масштабируется, так что ее наклон на $у = 0$ совпадает с наклоном $логит$ . Как результат, пробит модели иногда используются вместо модели logit потому что для некоторых приложений (например, в Байесовская статистика) реализация проще.

Смотрите также

Сигмовидная функция, обратная логит-функции
Дискретный выбор для двоичного логита, полиномиального логита, условного логита, вложенного логита, смешанного логита, разнесенного логита и упорядоченного логита
Ограниченная зависимая переменная
Дэниел Макфадден, а Нобелевская премия по экономике победитель за разработку той или иной логит-модели, используемой в экономике^[3]
Логит-анализ в маркетинге
Полиномиальный логит
Ogee, кривая аналогичной формы
Перцептрон
Пробит, другая функция с тем же доменом и диапазоном, что и логит
Оценка ридита
Преобразование данных (статистика)
Arcsin (преобразование)

использованная литература

^ «КОЭФФИЦИЕНТ СЧЕТОВ ЛОГА». nist.gov.
^ «Логит / Пробит» (PDF).
^ ^а ^б Дж. С. Крамер (2003). «Истоки и развитие логит-модели» (PDF). Кембридж UP.
^ Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 г.. Кембридж, Массачусетс: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.CS1 maint: ref = harv (ссылка на сайт)
^ Хильбе, Джозеф М. (2009), Модели логистической регрессии, CRC Press, стр. 3, ISBN 9781420075779.
^ Крамер, Дж. С. (2003), Логит-модели из экономики и других областей, Cambridge University Press, стр. 13, ISBN 9781139438193.
^ «Архивная копия». Архивировано из оригинал на 2011-07-06. Получено 2011-02-18.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
^ Трун, Себастьян (2003). «Изучение сеточных карт занятости с моделями переднего датчика». Автономные роботы. 15 (2): 111–127. Дои:10.1023 / А: 1025584807625. ISSN 0929-5593.
^ Стилер, Алекс (2012). «Статистические методы в робототехнике» (PDF). п. 2. Получено 2017-01-26.
^ Dickmann, J .; Appenrodt, N .; Klappstein, J .; Bloecher, H.L .; Muntzinger, M .; Sailer, A .; Hahn, M .; Бренк, К. (01.01.2015). "Заставить Берту увидеть еще больше: вклад радаров". Доступ IEEE. 3: 1233–1247. Дои:10.1109 / ACCESS.2015.2454533. ISSN 2169-3536.

дальнейшее чтение

Эштон, Уинифред Д. (1972). Логит-трансформация: с особым упором на его использование в биотесте. Статистические монографии и курсы Гриффина. 32. Чарльз Гриффин. ISBN 978-0-85264-212-2.

[1] «КОЭФФИЦИЕНТ СЧЕТОВ ЛОГА». nist.gov.

[2] «Логит / Пробит» (PDF).

[Cramer2003-3] а ^б Дж. С. Крамер (2003). «Истоки и развитие логит-модели» (PDF). Кембридж UP.

[4] Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 г.. Кембридж, Массачусетс: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.CS1 maint: ref = harv (ссылка на сайт)

[5] Хильбе, Джозеф М. (2009), Модели логистической регрессии, CRC Press, стр. 3, ISBN 9781420075779.

[6] Крамер, Дж. С. (2003), Логит-модели из экономики и других областей, Cambridge University Press, стр. 13, ISBN 9781139438193.

[7] «Архивная копия». Архивировано из оригинал на 2011-07-06. Получено 2011-02-18.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)

[8] Трун, Себастьян (2003). «Изучение сеточных карт занятости с моделями переднего датчика». Автономные роботы. 15 (2): 111–127. Дои:10.1023 / А: 1025584807625. ISSN 0929-5593.

[9] Стилер, Алекс (2012). «Статистические методы в робототехнике» (PDF). п. 2. Получено 2017-01-26.

[10] Dickmann, J .; Appenrodt, N .; Klappstein, J .; Bloecher, H.L .; Muntzinger, M .; Sailer, A .; Hahn, M .; Бренк, К. (01.01.2015). "Заставить Берту увидеть еще больше: вклад радаров". Доступ IEEE. 3: 1233–1247. Дои:10.1109 / ACCESS.2015.2454533. ISSN 2169-3536.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Navigation