WikiDer > Выбор материала

Material selection

Выбор материала это шаг в процессе проектирования любого физического объекта. В контексте дизайн продукта, основная цель выбора материала - минимизировать затраты при достижении целевых показателей производительности продукта.^[1] Систематический отбор лучшего материала для конкретной области применения начинается с свойства и стоимость кандидатских материалов. При выборе материала часто используется индекс материала или индекс производительности, соответствующий желаемым свойствам материала.^[2] Например, тепловое одеяло должно иметь плохой теплопроводность для минимизации теплопередачи при заданной разнице температур. Крайне важно, чтобы дизайнер хорошо знал свойства материалов и их поведение в рабочих условиях. Некоторые из важных характеристик материалов: прочность, долговечность, гибкость, вес, устойчивость к нагреву и коррозии, способность к литью, сварке или закалке, обрабатываемость, электропроводность и т. Д.^[3]

Систематический отбор приложений, требующих нескольких критериев, более сложен. Например, когда материал должен быть одновременно жестким и легким, для стержня сочетание высоких Модуль для младших и низкий плотность указывает лучший материал, тогда как для пластины кубический корень жесткости, деленной на плотность ${displaystyle {sqrt [{3}] {E}} / ho}$ является лучшим показателем, поскольку жесткость пластины на изгиб зависит от ее толщины в кубе. Точно так же, снова учитывая жесткость и легкость стержня, который будет растягиваться, удельный модуль, или модуль, деленный на плотность ${displaystyle E / ho}$ следует учитывать, тогда как для балки, которая будет подвергаться изгибу, показатель материала ${displaystyle {sqrt [{2}] {E}} / ho}$ лучший индикатор.

Реальность часто имеет ограничения, и необходимо учитывать утилитарный фактор. Стоимость идеального материала, в зависимости от формы, размера и состава, может быть непомерно высокой, а спрос, общность часто используемых и известных предметов, его характеристики и даже регион рынка определяют его доступность.

Участки Эшби

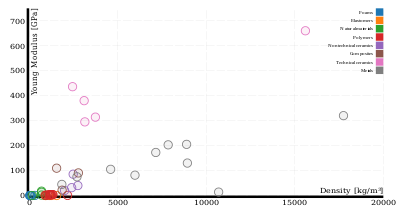
График зависимости модуля Юнга от плотности. Цвета представляют семейства материалов.

Заговор Эшби, названный в честь Майкл Эшби из Кембриджский университет, представляет собой диаграмму рассеяния, которая отображает два или более свойств многих материалов или классов материалов.^[4] Эти графики полезны для сравнения соотношения между различными свойствами. Например, жесткая / легкая часть, описанная выше, будет иметь модуль Юнга на одной оси и плотность на другой оси, с одной точкой данных на графике для каждого материала-кандидата. На таком участке легко найти материал не только с наибольшей жесткостью или наименьшей плотностью, но и с наилучшим соотношением ${displaystyle E / ho}$ . Использование логарифмической шкалы по обеим осям облегчает выбор материала с наилучшей жесткостью листа. ${displaystyle {sqrt [{3}] {E}} / ho}$ .

График зависимости модуля Юнга от плотности с логарифмическим масштабированием. Цвета представляют семейства материалов.

Первый график справа показывает плотность и модуль Юнга в линейном масштабе. Второй график показывает те же атрибуты материалов в логарифмической шкале. Семейства материалов (полимеры, пена, металлы и т. Д.) Обозначаются цветом.

Вопросы стоимости

Стоимость материалов играет очень важную роль при их выборе. Самый простой способ сопоставить стоимость со свойствами - это разработать денежную метрику для свойств деталей. Например, оценка жизненного цикла может показать, что чистая приведенная стоимость Уменьшение веса автомобиля на 1 кг в среднем составляет около 5 долларов, поэтому замена материала, уменьшающая вес автомобиля, может стоить до 5 долларов за килограмм снижения веса дороже, чем исходный материал.^{[нужна цитата]} Однако географическая и временная зависимость затрат на энергию, техническое обслуживание и другие эксплуатационные расходы, а также различия в ставках дисконтирования и схемах использования (расстояние, пройденное за год в этом примере) между отдельными лицами означает, что для этого не существует единого правильного числа. Для коммерческих самолетов это число ближе к 450 долл. США / кг, а для космических аппаратов стоимость запуска составляет около 20 000 долл. США / кг.^[5]

Таким образом, по мере роста цен на энергоносители и совершенствования технологий автомобили заменяли все большее количество легких магний и алюминиевые сплавы для сталь, самолеты заменяют пластик, армированный углеродным волокном и титановые сплавы для алюминия и спутники давно сделаны из экзотики композитные материалы.

Конечно, стоимость килограмма - не единственный важный фактор при выборе материала. Важное понятие - «стоимость единицы функции». Например, если ключевой целью проектирования была жесткость пластины из материала, как описано во вводном параграфе выше, то проектировщику потребуется материал с оптимальным сочетанием плотности, модуля Юнга и цены. Оптимизация сложных комбинаций технических и ценовых характеристик - сложный процесс, который необходимо выполнить вручную, поэтому программное обеспечение для рационального выбора материалов является важным инструментом.

Общий метод использования диаграммы Эшби

Использование «диаграммы Эшби» - распространенный метод выбора подходящего материала. Во-первых, идентифицируются три различных набора переменных:

Переменные материала неотъемлемые свойства материала, такие как плотность, модуль, предел текучести, и многие другие.
Свободные переменные - это величины, которые могут изменяться во время цикла нагружения, например, приложенная сила.
Переменные конструкции - это ограничения, накладываемые на конструкцию, например, насколько толстой может быть балка или насколько она может отклоняться.

Затем уравнение для индекс производительности выводится. Это уравнение количественно определяет, насколько желательным будет материал для конкретной ситуации. По соглашению, более высокий индекс производительности означает лучший материал. Наконец, индекс производительности нанесен на диаграмму Эшби. Визуальный осмотр позволяет выявить наиболее желаемый материал.

Пример использования диаграммы Эшби

В этом примере на материал будет распространяться как растяжение, так и изгиб. Следовательно, оптимальный материал будет работать в обоих случаях.

Индекс производительности при напряжении

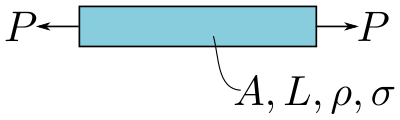
В первом случае на балку действуют две силы: сила тяжести. ${displaystyle w}$ и напряжение ${displaystyle P}$ . Переменные материала - плотность ${displaystyle ho}$ и прочность ${displaystyle sigma}$ . Предположим, что длина ${displaystyle L}$ и напряжение ${displaystyle P}$ фиксированы, что делает их проектными переменными. Наконец, площадь поперечного сечения ${displaystyle A}$ это свободная переменная. Задача в этой ситуации - минимизировать вес ${displaystyle w}$ путем выбора материала с наилучшим сочетанием переменных материалов ${displaystyle ho, sigma}$ . Рисунок 1 иллюстрирует эту нагрузку.

Рисунок 1. Балка под нагрузкой растягивающего напряжения для минимизации веса.

Напряжение в балке измеряется как ${displaystyle P / A}$ тогда как вес описывается ${displaystyle w = ho AL}$ . Получение индекса производительности требует, чтобы все свободные переменные были удалены, оставив только переменные конструкции и переменные материала. В данном случае это означает, что ${displaystyle A}$ необходимо удалить. Уравнение осевого напряжения можно переформулировать так: ${displaystyle A = P / sigma}$ . Подставляя это в уравнение веса, получаем ${displaystyle w = ho (P / sigma) L = ho LP / sigma}$ . Затем переменные материала и проектные переменные группируются отдельно, что дает ${displaystyle w = (ho / sigma) LP}$ .

Поскольку оба ${displaystyle L}$ и ${displaystyle P}$ фиксированы, а поскольку цель - минимизировать ${displaystyle w}$ , то отношение ${displaystyle ho / sigma}$ следует свести к минимуму. Однако по соглашению индекс производительности всегда является величиной, которую следует максимизировать. Следовательно, полученное уравнение имеет вид ${displaystyle {ext {Performance index}} = P_ {cr} = sigma / ho}$

Показатель производительности при гибке

Затем предположим, что материал также подвергается изгибающим силам. Уравнение максимального растягивающего напряжения при изгибе: ${displaystyle sigma = (- My) / I}$ , где ${displaystyle M}$ это изгибающий момент, ${displaystyle y}$ - расстояние от нейтральной оси, а ${displaystyle I}$ момент инерции. Это показано на рисунке 2. Используя приведенное выше уравнение весов и решив для свободных переменных, мы пришли к следующему решению: ${displaystyle w = {sqrt {6MbL ^ {2}}} (ho / {sqrt {sigma}})}$ , где ${displaystyle L}$ это длина и ${displaystyle b}$ высота балки. При условии, что ${displaystyle b}$ , ${displaystyle L}$ , и ${displaystyle M}$ являются фиксированными проектными переменными, индекс производительности для гибки становится ${displaystyle P_ {CR} = {sqrt {sigma}} / ho}$ .

Фигура 2. Балка при изгибе. Попытка уменьшить вес

Выбор лучшего материала в целом

На этом этапе были выведены два показателя производительности: для натяжения ${displaystyle sigma / ho}$ и для гибки ${displaystyle {sqrt {sigma}} / ho}$ . Первый шаг - создать логарифмический график и добавьте все известные материалы в соответствующие места. Тем не менее, уравнения индекса производительности должны быть изменены, прежде чем они будут нанесены на логарифмический график.

Для уравнения характеристик натяжения ${displaystyle P_ {CR} = sigma / ho}$ , первый шаг - сделать журнал с обеих сторон. Полученное уравнение может быть переставил давать ${displaystyle log (sigma) = log (ho) + log (P_ {CR})}$ . Обратите внимание, что это соответствует формату ${displaystyle y = x + b}$ , что делает его линейным на логарифмическом графе. Точно так же пересечение оси Y - это логарифм ${displaystyle P_ {CR}}$ . Таким образом, фиксированное значение ${displaystyle P_ {CR}}$ для натяжения на Рисунке 3 - 0,1.

Уравнение характеристик изгиба ${displaystyle P_ {CR} = {sqrt {sigma}} / ho}$ можно рассматривать аналогично. С использованием степенное свойство логарифмов можно вывести, что ${displaystyle log (sigma) = 2 imes (log (ho) + log (P_ {CR}))}$ . Значение для ${displaystyle P_ {CR}}$ для изгиба составляет ≈ 0,0316 на рисунке 3. Наконец, обе линии нанесены на диаграмму Эшби.

Рисунок 3. Диаграмма Эшби с показателями производительности, построенными для максимального результата

Во-первых, лучшие материалы для гибки можно найти, изучив, какие области на графике выше, чем ${displaystyle {sqrt {sigma}} / ho}$ линия изгиба. В этом случае часть пенопласта (синяя) и техническая керамика (розовая) выше линии. Следовательно, это будут лучшие материалы для гибки. Напротив, материалы, которые находятся далеко ниже линии (например, металлы в правом нижнем углу серой области), будут худшими материалами.

Наконец, ${displaystyle sigma / ho}$ Линию натяжения можно использовать для «разрыва связи» между пеной и технической керамикой. Поскольку техническая керамика - единственный материал, который располагается выше линии натяжения, то лучше всего подходит техническая керамика. Таким образом, лучшим материалом в целом является техническая керамика в верхнем левом углу розовой области, например карбид бора.

Численное понимание диаграммы

Затем индекс производительности можно отобразить на диаграмме Эшби, преобразовав уравнение в логарифмическую шкалу. Для этого нужно взять бревно с обеих сторон и построить его, как линию с ${displaystyle P_ {cr}}$ является точкой пересечения оси Y. Это означает, что чем выше перехват, тем выше характеристики материала. При перемещении линии вверх по диаграмме Эшби индекс производительности становится выше. Каждый материал, через который проходит линия, имеет индекс производительности, указанный на оси ординат. Таким образом, перемещение к верхней части диаграммы, при этом все еще касаясь области материала, - это самая высокая производительность.

Как видно из рисунка 3, две линии пересекаются в верхней части графика в разделе «Техническая керамика» и «Композиты». Это даст индекс производительности 120 для нагрузки на растяжение и 15 для изгиба. Принимая во внимание стоимость инженерной керамики, особенно потому, что точка пересечения находится вокруг карбида бора, это не будет оптимальным случаем. Лучший вариант с более низким индексом производительности, но более экономичными решениями - это инженерные композиты рядом с углепластиком.

использованная литература

^ Джордж Э. Дитер (1997). «Обзор процесса выбора материалов», Справочник ASM Том 20: Выбор материалов и проектирование.
^ Эшби, М. Ф. (1999). Выбор материалов в механическом проектировании (2-е изд.). Оксфорд, Оксфорд: Баттерворт-Хайнеманн. п. 407. ISBN 0-7506-4357-9. OCLC 49708474.
^ Общие соображения по конструкции машины В архиве 2019-04-15 в Wayback Machine, Сообщество инженеров-механиков и обсуждение, получено 15 апреля 2018 г.
^ Эшби, Майкл (1999). Выбор материалов в механическом проектировании (3-е изд.). Берлингтон, Массачусетс: Баттерворт-Хайнеманн. ISBN 0-7506-4357-9.
^ Эшби, Майкл Ф. (2005). Выбор материалов в механическом проектировании. США: Elsevier Ltd. стр. 251. ISBN 978-0-7506-6168-3.

[1] Джордж Э. Дитер (1997). «Обзор процесса выбора материалов», Справочник ASM Том 20: Выбор материалов и проектирование.

[2] Эшби, М. Ф. (1999). Выбор материалов в механическом проектировании (2-е изд.). Оксфорд, Оксфорд: Баттерворт-Хайнеманн. п. 407. ISBN 0-7506-4357-9. OCLC 49708474.

[3] Общие соображения по конструкции машины В архиве 2019-04-15 в Wayback Machine, Сообщество инженеров-механиков и обсуждение, получено 15 апреля 2018 г.

[ashby-4] Эшби, Майкл (1999). Выбор материалов в механическом проектировании (3-е изд.). Берлингтон, Массачусетс: Баттерворт-Хайнеманн. ISBN 0-7506-4357-9.

[5] Эшби, Майкл Ф. (2005). Выбор материалов в механическом проектировании. США: Elsevier Ltd. стр. 251. ISBN 978-0-7506-6168-3.

[1]

[2]

[3]

[4]

[5]

Navigation